锂电池SOC估计基于二阶RC模型的扩展卡尔曼滤波估算SOC 验证工况：HPPC 和

原创于 2025-12-07 11:45:00 发布 · 175 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#bash

锂电池SOC估计基于二阶RC模型的扩展卡尔曼滤波估算SOC 验证工况：HPPC 和 1C放电

锂电池SOC估计这玩意儿说难不难，但真要实操起来到处都是坑。今天咱们就拿二阶RC模型开刀，用扩展卡尔曼滤波（EKF）整点实在的。先甩个模型结构图镇楼——等效电路里藏着两个RC环节，专门对付电池的动态特性，比一阶模型能多抓点极化效应。

先上硬菜，模型的状态方程得离散化处理。代码里这个predict_state函数看着简单，实际上藏着非线性变换的玄机：

def predict_state(soc, v1, v2, current, dt, R1, C1, R2, C2):
    soc_new = soc - dt/(3600*capacity) * current
    v1_new = np.exp(-dt/(R1*C1)) * v1 + R1*(1 - np.exp(-dt/(R1*C1))) * current
    v2_new = np.exp(-dt/(R2*C2)) * v2 + R2*(1 - np.exp(-dt/(R2*C2))) * current
    return soc_new, v1_new, v2_new

这里的三行代码处理了SOC和两个极化电压的更新。注意指数项里的时间常数处理，R1C1和R2C2这两个时间常数要是没辨识准，整个模型直接翻车。

雅可比矩阵的计算是EKF的灵魂，特别是对OCV-SOC曲线的求导。实验室老司机都懂，这里用spline插值比多项式拟合稳得多：

from scipy.interpolate import UnivariateSpline

ocv_spline = UnivariateSpline(soc_data, ocv_data, s=0)
dOCV_dSOC = ocv_spline.derivative()

实测某三元电池的dOCV/dSOC曲线在30%SOC附近斜率能达到80mV/%，这个陡峭区域就是EKF发力的黄金地段。但碰到SOC在50%左右的平台区，卡尔曼增益立马怂成狗，这时候就得靠模型精度硬扛了。

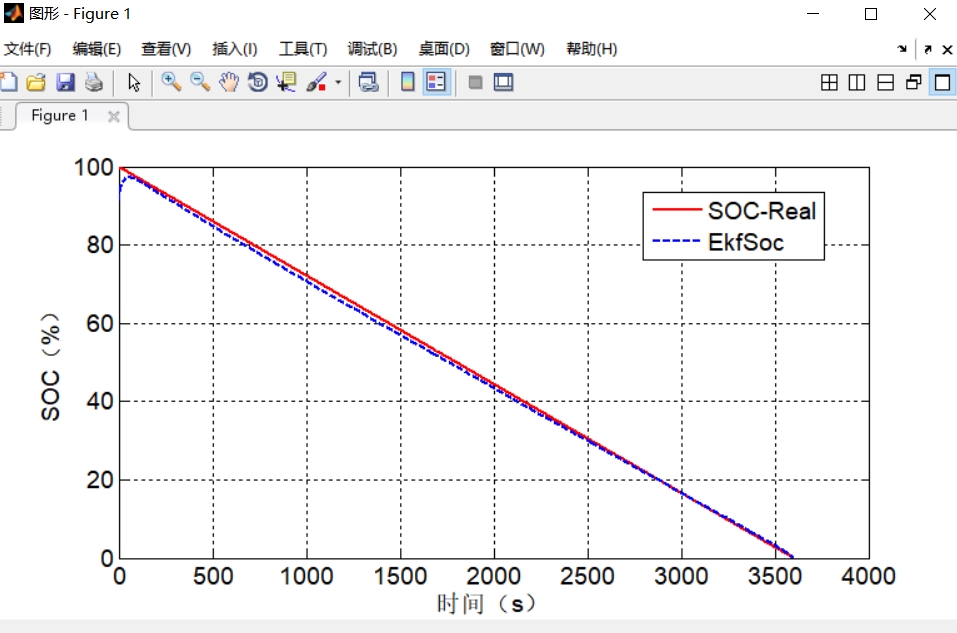
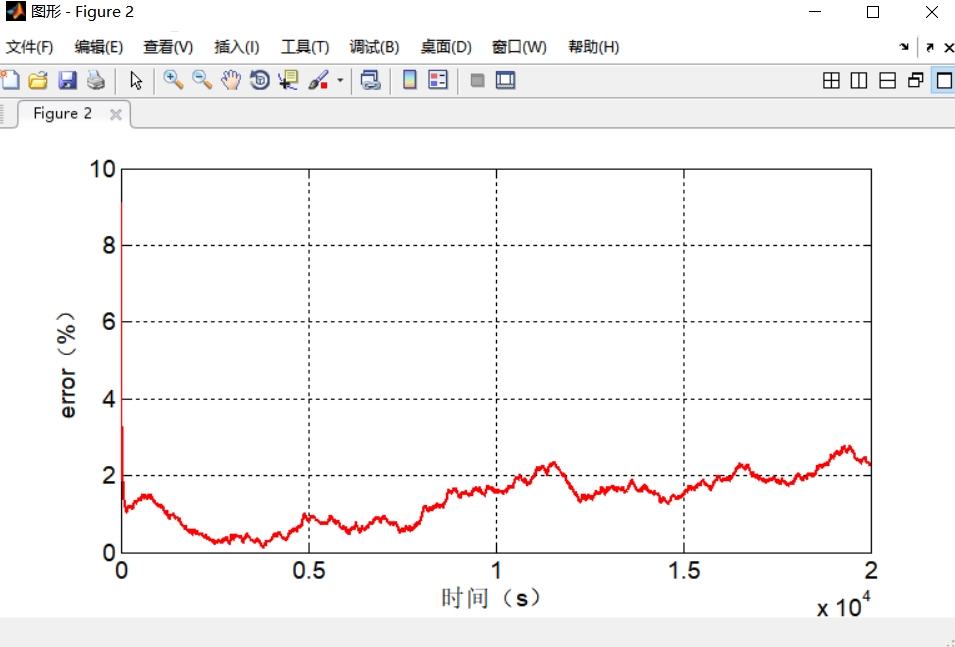
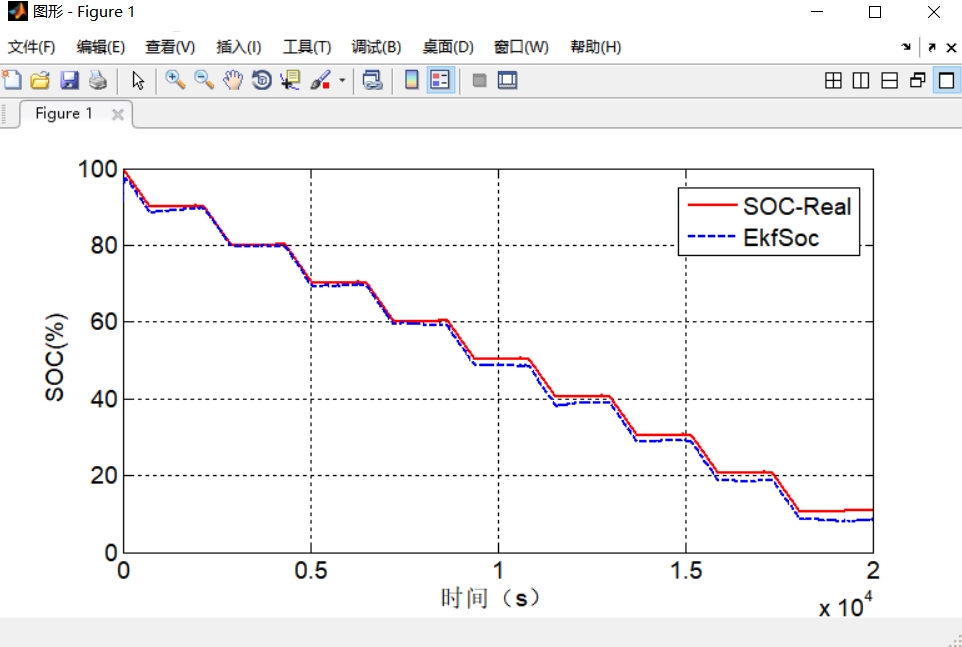
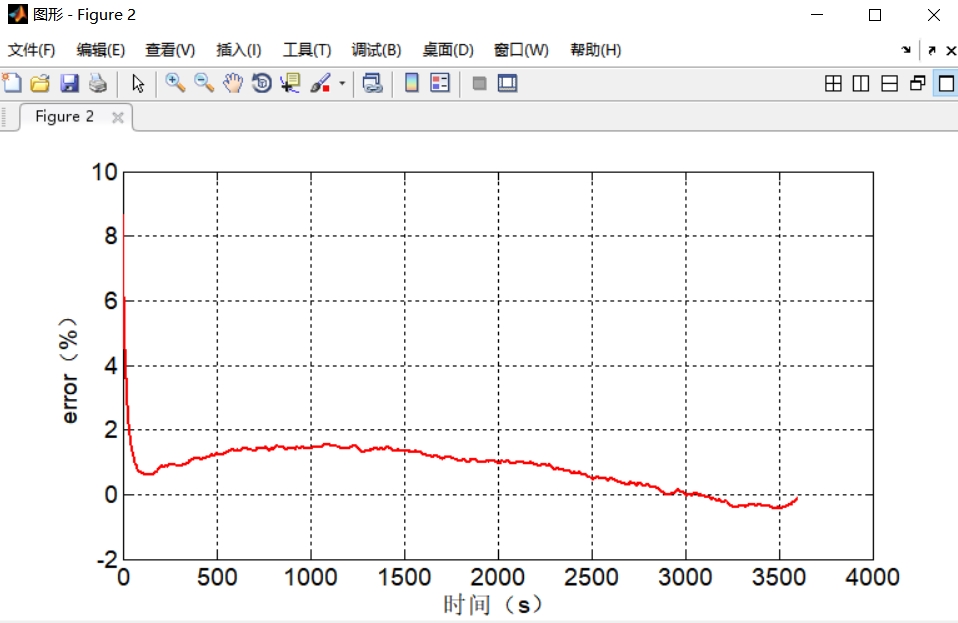
跑HPPC工况验证时发现个反直觉的现象——脉冲放电时的SOC估计误差反而比静置时小。盯着协方差矩阵的变化才明白，剧烈电流波动给系统带来了更多观测信息。反倒是1C恒流放电时，误差会像温水煮青蛙一样慢慢累积，这时候自适应噪声协方差的trick就派上用场了。

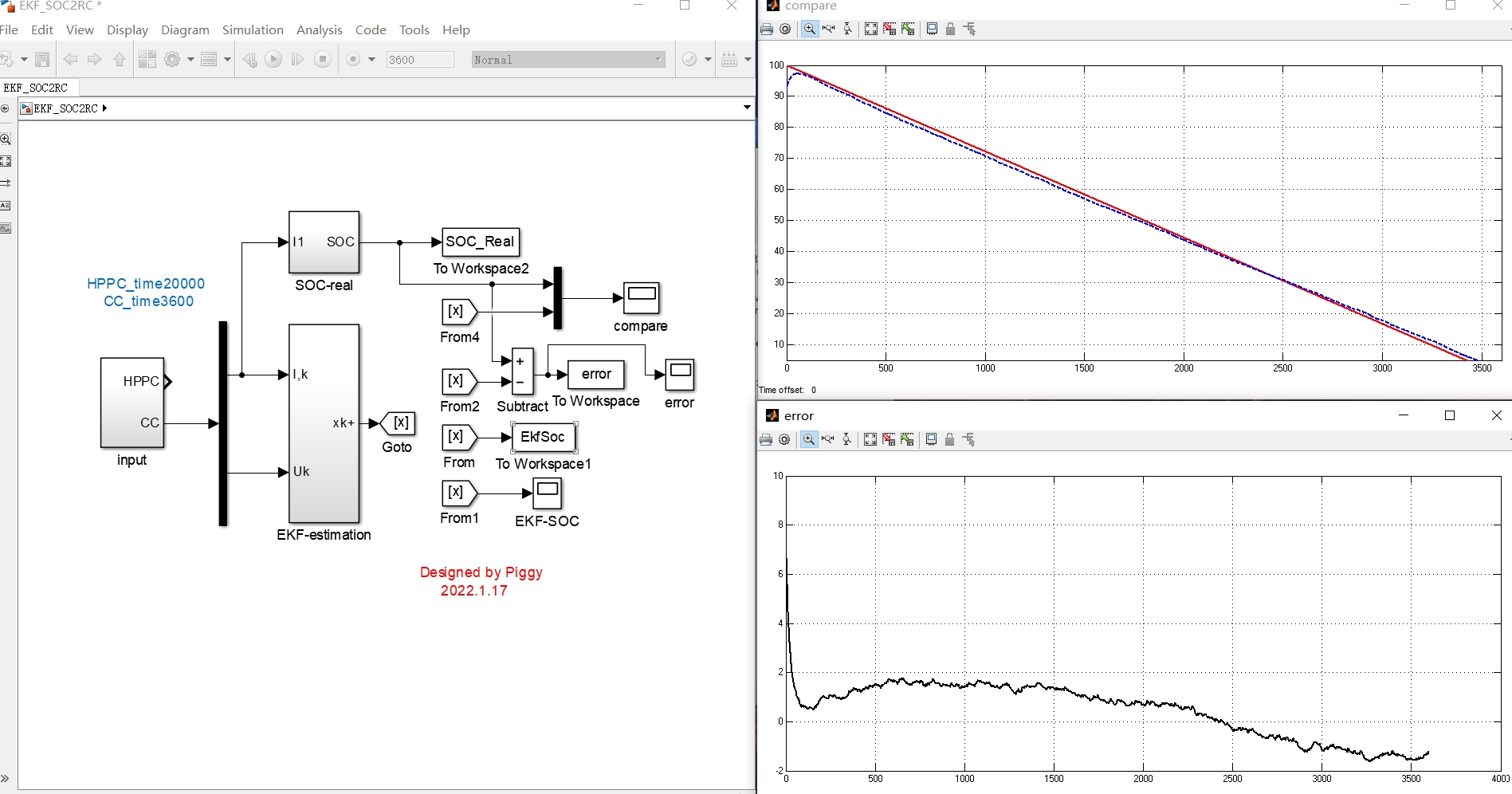
最后给个实战建议：别死磕EKF的参数整定，先把HPPC测试做扎实。模型参数随SOC变化搞个二维查表，比用固定参数估计精度能提升至少3个百分点。另外测量噪声协方差矩阵别设太小，留点余量给传感器误差，毕竟BMS采集的电流波动比实验室设备野多了。