基于拓展卡尔曼滤波的车辆质量与道路坡度估计 车辆坡度与质量识别模型,基于扩展卡尔曼滤波,估计曲线与实际误差合理。 先用递归最小二乘法(RLS)质量识别,最后利用扩展卡尔曼坡度识别(EKF)。 送纹献 Matlab/simulink模型 2019以上版本
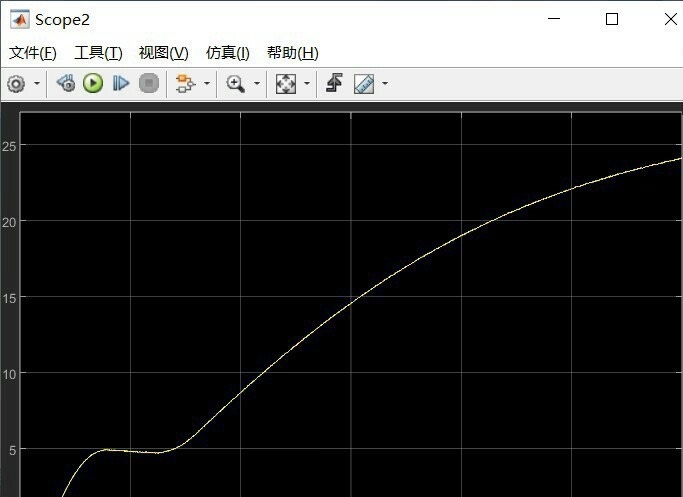
直接在Simulink里搭车辆模型的时候,最头疼的就是参数耦合问题。比如说车辆质量和道路坡度这两个变量,在纵向动力学方程里经常互相影响。这时候用扩展卡尔曼滤波(EKF)配合递归最小二乘法(RLS),实测效果比单用传统方法靠谱不少。
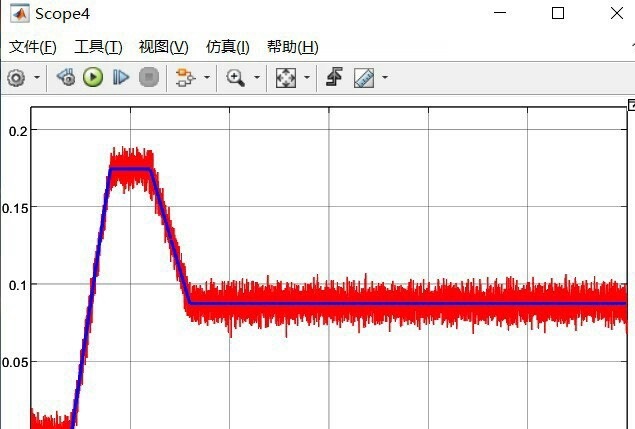
先看质量估计部分,用RLS的核心在于实时更新参数。这里有个关键——加速度信号的质量直接影响估计精度。我通常会先对原始信号做滑动平均滤波:
accel_filtered = filter(ones(1,5)/5, 1, accel_raw);这个5点移动平均能有效消除高频噪声又不明显滞后。RLS初始化时,协方差矩阵P的初始值别设太小,容易导致初期震荡。建议从1e4开始:
P = 1e4 * eye(2);
lambda = 0.98; % 遗忘因子执行参数更新时要注意矩阵维数匹配。特别是当采样时间不固定时,得用时间差dt动态调整:
phi = [accel_filtered(k), g*sin(theta_est)]; % 回归向量
K = P * phi' / (lambda + phi * P * phi');
m_est = m_est_prev + K * (F_drive(k) - phi*m_est_prev);
P = (eye(2) - K*phi) * P / lambda;这里theta_est是当前坡度估计值,实际运行时需要和EKF模块交互数据。有个坑是当车辆静止时加速度信号失效,这时候得暂停参数更新。
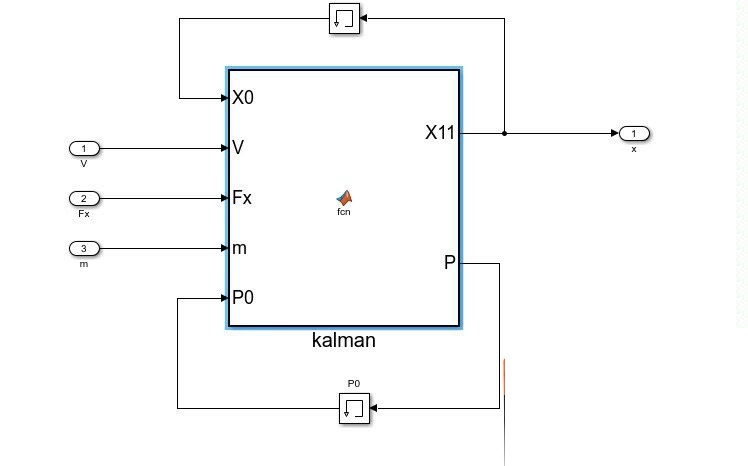
转到EKF坡度估计时,状态方程要考虑质量估计值的变化。状态变量选为速度和坡度:
function x_pred = ekfStateFcn(x)
v = x(1);
theta = x(2);
dv = (F_drive - c_resistance*v^2)/m_est - g*sin(theta);
dtheta = 0; % 假设坡度变化缓慢
x_pred = [v + dv*dt;
theta + dtheta*dt];
end观测方程处理GPS速度信号时,注意单位转换。实际项目中遇到过美国团队用mph而国内用km/h导致的乌龙事件:
function z = ekfMeasFcn(x)
z = x(1) * 3.6; % m/s转km/h
end协方差矩阵Q和R需要现场调参。有个小技巧:在平路上空载运行时记录噪声水平,取方差值的2-3倍作为初始值。调试时开着动画看估计曲线特别直观:
simOut = sim('vehicle_estimation_model');
plot(simOut.theta_est.Time, simOut.theta_est.Data*180/pi, 'r--');
hold on;
plot(simOut.theta_true.Time, simOut.theta_true.Data*180/pi, 'b-');实测中发现当坡度超过10%时,轮胎滑移率会影响估计精度。这时候在测量方程里加入滑移率补偿项效果立竿见影。不过具体补偿系数得看轮胎特性,冬季胎和夏季胎的修正系数能差30%以上。
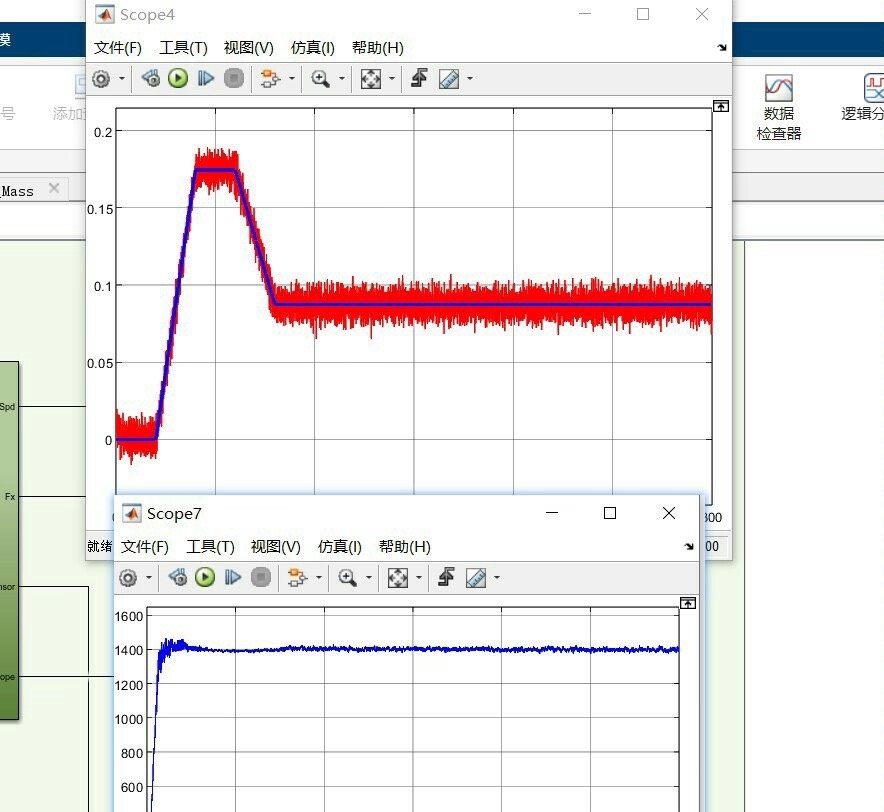
最后在模型验证阶段,建议构造三角波变化的虚拟坡度信号。观察估计值跟踪滞后情况,适当调整EKF的过程噪声参数。质量估计误差控制在±5%以内,坡度估计在±1°范围内,基本能满足多数控制系统的需求。




















 431
431

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








