100kW 光伏并网发电系统 MATLAB 仿真模型探索

原创于 2025-12-03 13:38:49 发布 · 583 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#xbox

100kW光伏并网发电系统MATLAB仿真模型采用“增量电导+积分调节器”技术的MPPT控制器 VSC并网控制

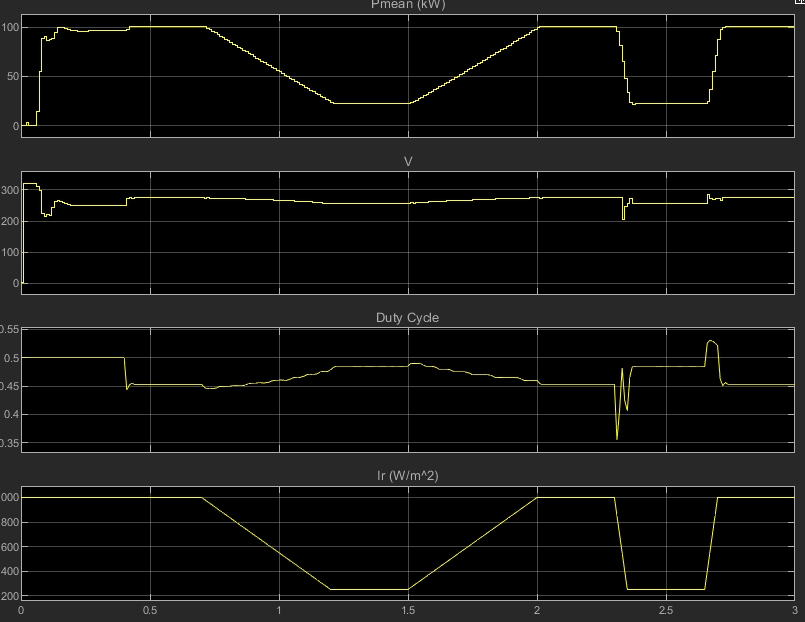
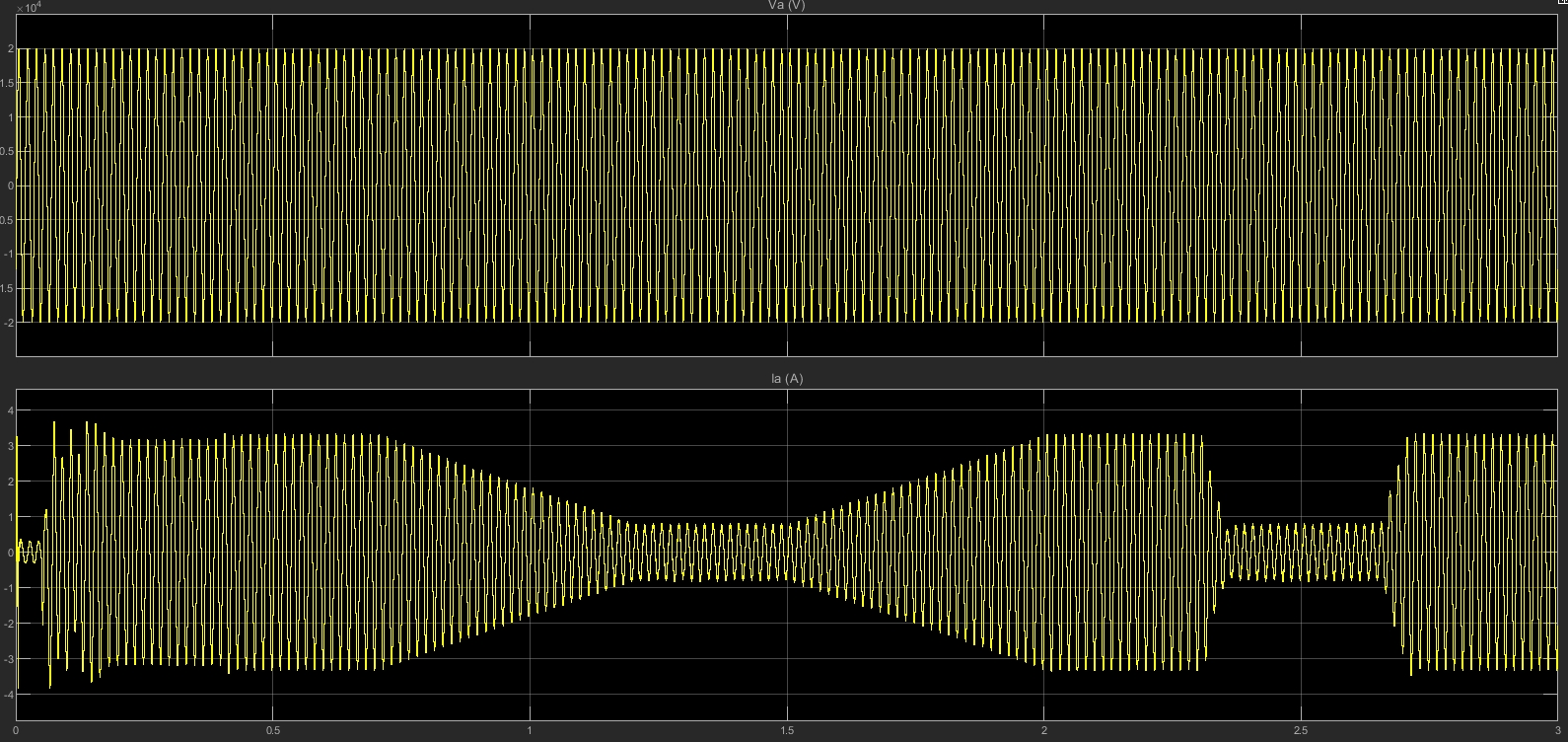
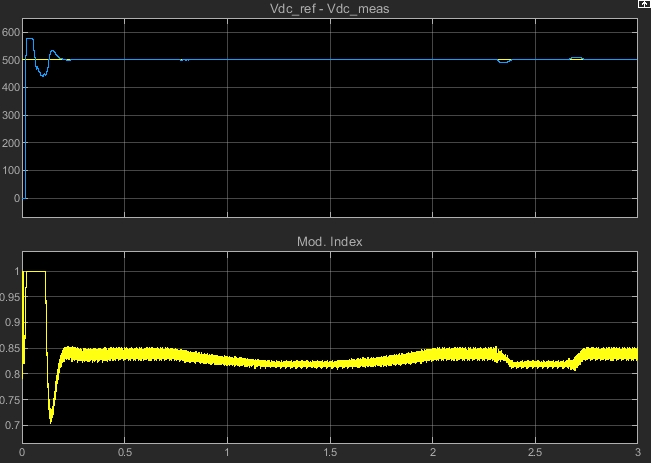
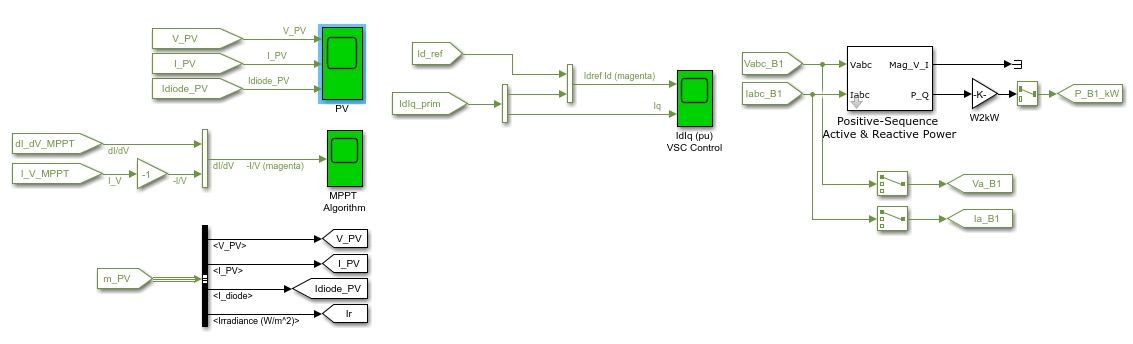
最近在研究光伏并网发电系统，搭建了一个 100kW 的 MATLAB 仿真模型，今天就来和大家分享下其中用到的关键技术。

“增量电导 + 积分调节器”技术的 MPPT 控制器

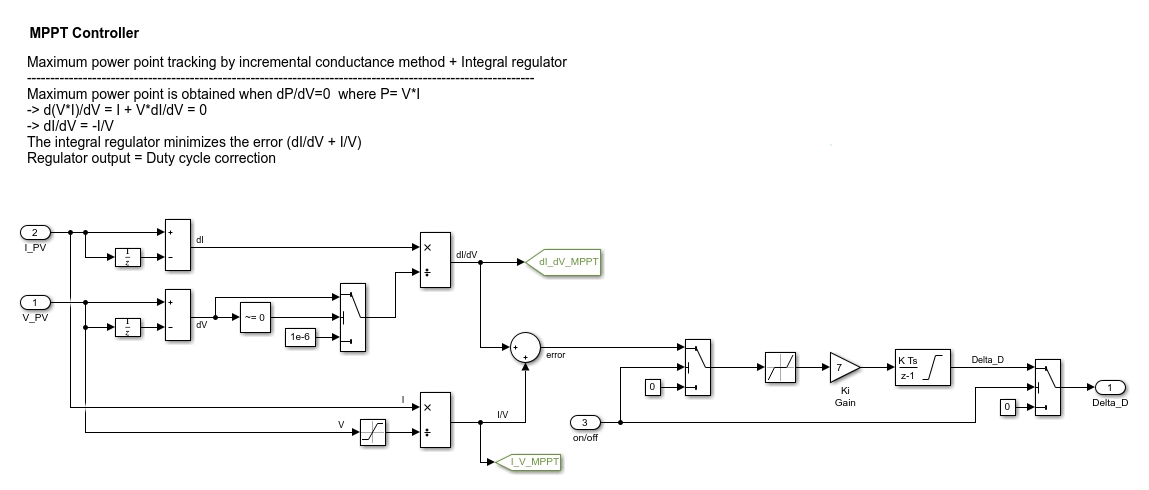
在光伏系统里，最大功率点跟踪（MPPT）控制器至关重要。我采用的是“增量电导 + 积分调节器”技术，这一组合能较为精准地跟踪光伏电池的最大功率点。

先来看下增量电导法的原理。我们知道，光伏电池的功率$P = U \times I$，对其求导可得$\frac{dP}{dU}=I + U\frac{dI}{dU}$。当$\frac{dP}{dU}=0$时，光伏电池工作在最大功率点。也就是说，当$I + U\frac{dI}{dU}=0$，即$\frac{dI}{dU}=-\frac{I}{U}$时，系统处于最大功率点状态。

用代码简单示意一下（这里只是关键部分伪代码，并非完整可运行代码）：

% 初始化参数
% 假设已经获取到当前的电压U和电流I
dU = 0.01; % 电压微小变化量
U_new = U + dU; 
I = getCurrent(U); % 假设这是获取对应电压下电流的函数
I_new = getCurrent(U_new); 
dI = I_new - I; 
if (dI/dU) == (-I/U)
    % 此时接近最大功率点，可做相应处理
    disp('接近最大功率点');
elseif (dI/dU) > (-I/U)
    % 需增大电压
    U = U + step_size; 
else
    % 需减小电压
    U = U - step_size; 
end

上述代码中，通过比较$\frac{dI}{dU}$和$-\frac{I}{U}$的大小关系，来决定是增大还是减小光伏电池的工作电压，从而逐渐逼近最大功率点。

再说说积分调节器，它能对系统的误差进行积分运算，有助于消除稳态误差，让系统能更稳定地跟踪最大功率点。假设误差$e$为最大功率点对应的电压与当前电压的差值，积分环节代码可类似这样写：

% 初始化积分项
integral_term = 0; 
K_i = 0.1; % 积分系数
e = reference_U - U; % 计算误差
integral_term = integral_term + e; 
U_adjust = K_i * integral_term; 
U = U + U_adjust;

这里通过不断累积误差，并乘以积分系数来调整电压，使得系统能更精准地跟踪最大功率点。“增量电导 + 积分调节器”技术结合，就像给光伏系统安装了一个智能的“能量追踪器”。

VSC 并网控制

VSC（Voltage Source Converter，电压源换流器）并网控制在光伏并网系统中也占据核心地位。它能够将光伏电池产生的直流电转换为与电网同频、同相的交流电，并实现功率的灵活控制。

VSC 并网控制的核心是对电流的精确控制。以dq 坐标系下的电流控制为例，首先要将三相静止坐标系下的电流$ia$，$ib$，$ic$通过 Clark 变换和 Park 变换转换到 dq 坐标系下，得到$id$和$i_q$。

% Clark变换
alpha = i_a;
beta = (sqrt(3)/3)*(i_b - i_c);
% Park变换
theta = getGridAngle(); % 获取电网角度的函数
i_d = alpha*cos(theta)+beta*sin(theta);
i_q = -alpha*sin(theta)+beta*cos(theta);

之后，根据电网的要求给定$id^$和$iq^$，通过PI调节器来调节电流，使得实际电流跟踪给定电流。

% PI调节器
K_p = 0.5; 
K_i = 0.01; 
e_d = i_d_star - i_d; 
e_q = i_q_star - i_q; 
integral_d = integral_d + e_d; 
integral_q = integral_q + e_q; 
v_d = K_p*e_d + K_i*integral_d; 
v_q = K_p*e_q + K_i*integral_q;

最后再通过反 Park 变换和反 Clark 变换，将 dq 坐标系下的电压转换回三相静止坐标系，用于控制 VSC 的开关管。

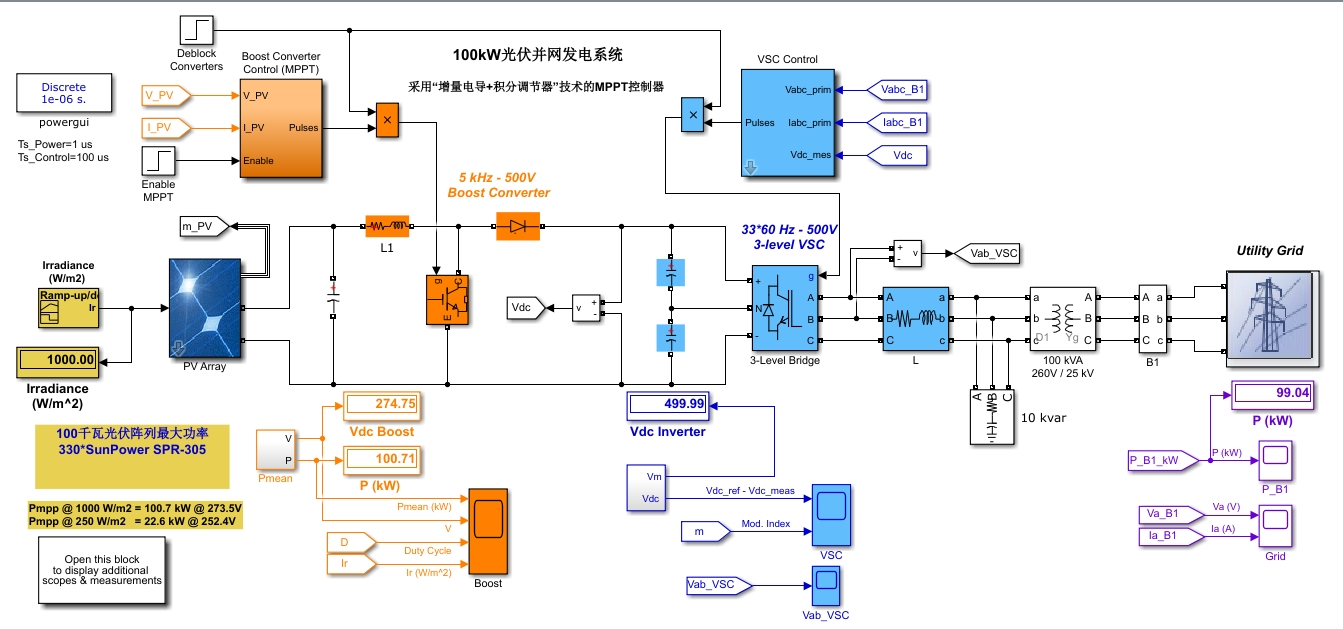
通过以上“增量电导 + 积分调节器”技术的 MPPT 控制器和 VSC 并网控制技术，构建的 100kW 光伏并网发电系统 MATLAB 仿真模型能较好地模拟实际的光伏并网运行情况。喜欢的可以自己研究，深入挖掘其中更多有趣的细节和优化方向。说不定在你的探索中，还能发现一些更巧妙的改进方法，为光伏并网技术的发展添砖加瓦呢！