基于死区补偿的永磁同步电机SVPWM控制仿真探索

基于死区补偿的永磁同步电机SVPWM控制仿真 死区的存在会产生高次谐波，引发转矩脉动，影响了电机的正常运行。 通过对SVPWM控制进行补偿的方式可以有效削弱死区带来的影响。 仿真搭建了使用死区补偿以及未使用死区补偿PMSM矢量控制的两套系统。 其中，死区补偿采用电流检测，判断角度逻辑，输出补偿角的方法实现。 学习相关内容的同学可以研究仿真配合相关文献进行学习。 全套资料包括： [1]完整仿真模型 [2]相关参考文献。

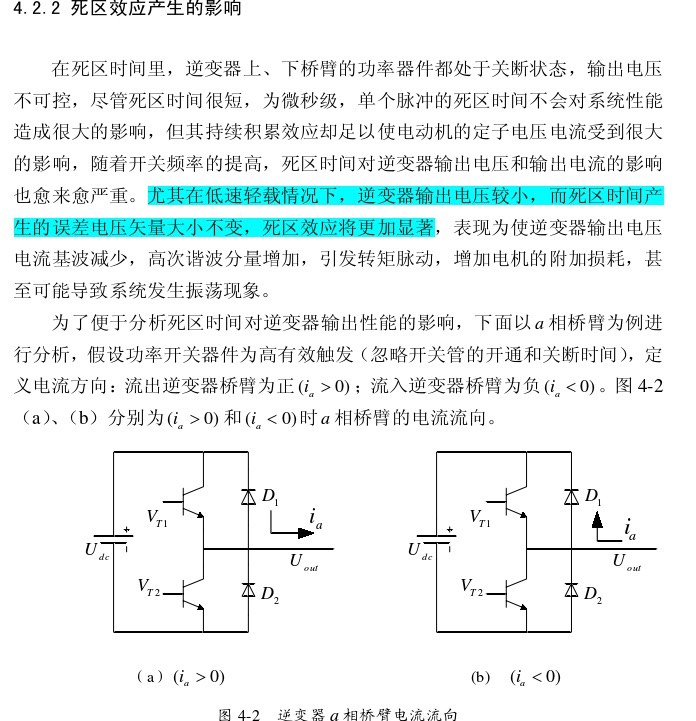
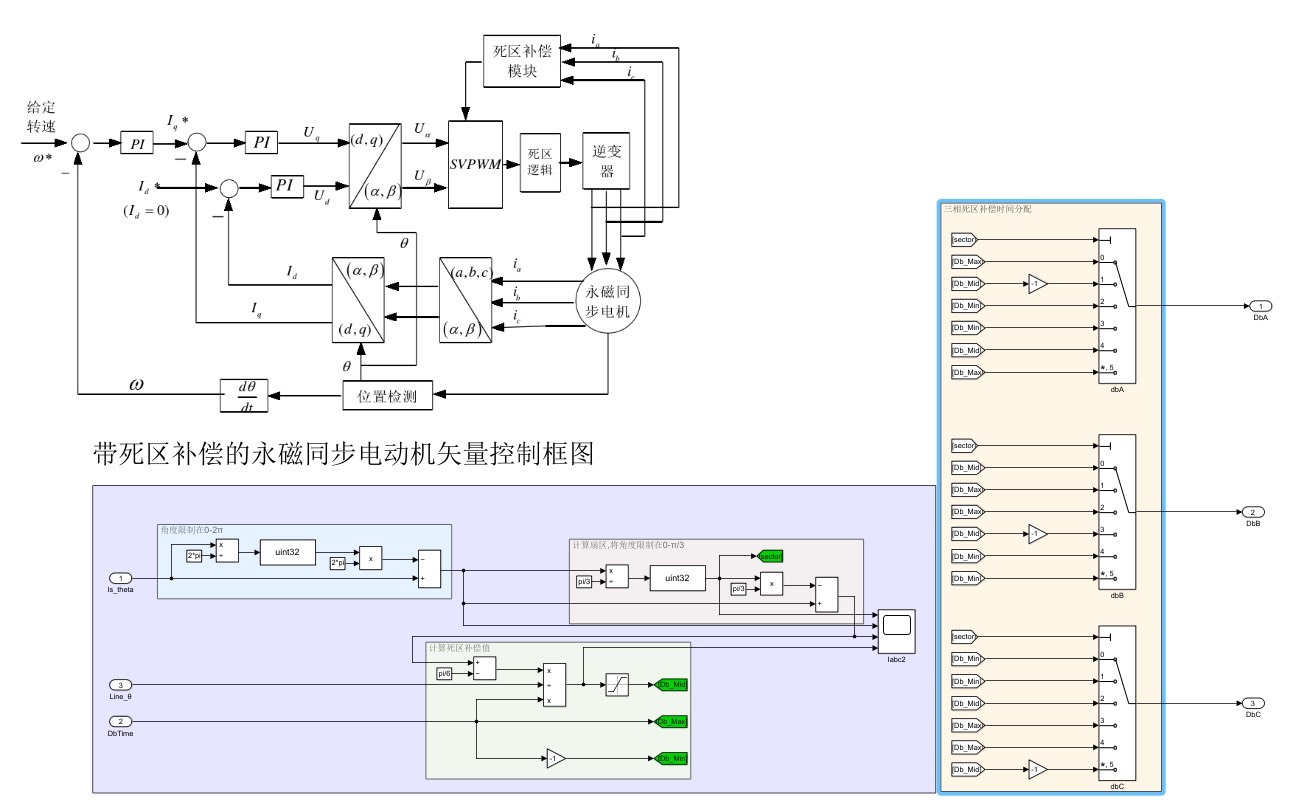
在永磁同步电机（PMSM）的控制领域，死区问题一直是影响电机性能的关键因素。死区的存在可不是个小麻烦，它会产生高次谐波，进而引发转矩脉动，使得电机无法正常、平稳地运行。想象一下，电机就像一个舞者，如果高次谐波和转矩脉动捣乱，那这个舞者的步伐就会变得凌乱，无法跳出优美的舞蹈。

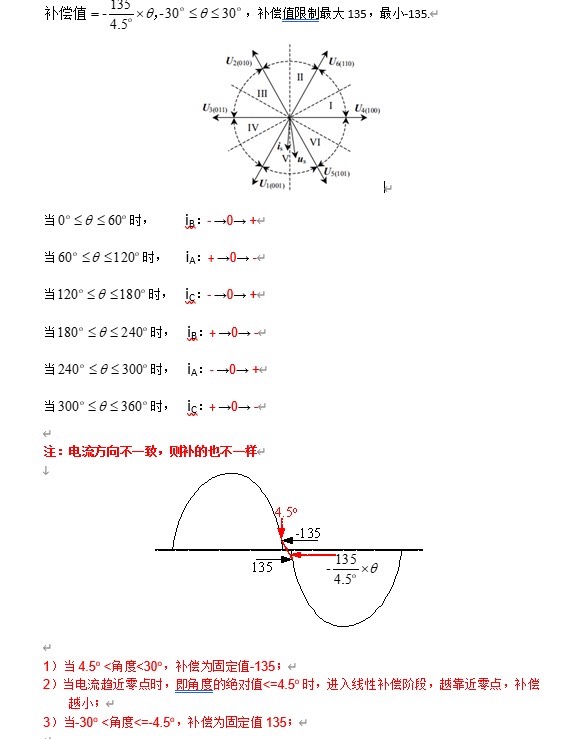
不过，聪明的工程师们找到了应对之策，那就是通过对空间矢量脉宽调制（SVPWM）控制进行补偿，以此有效削弱死区带来的负面影响。就好比给这个“舞者”穿上了一双合适的舞鞋，让它能够重新找回节奏。

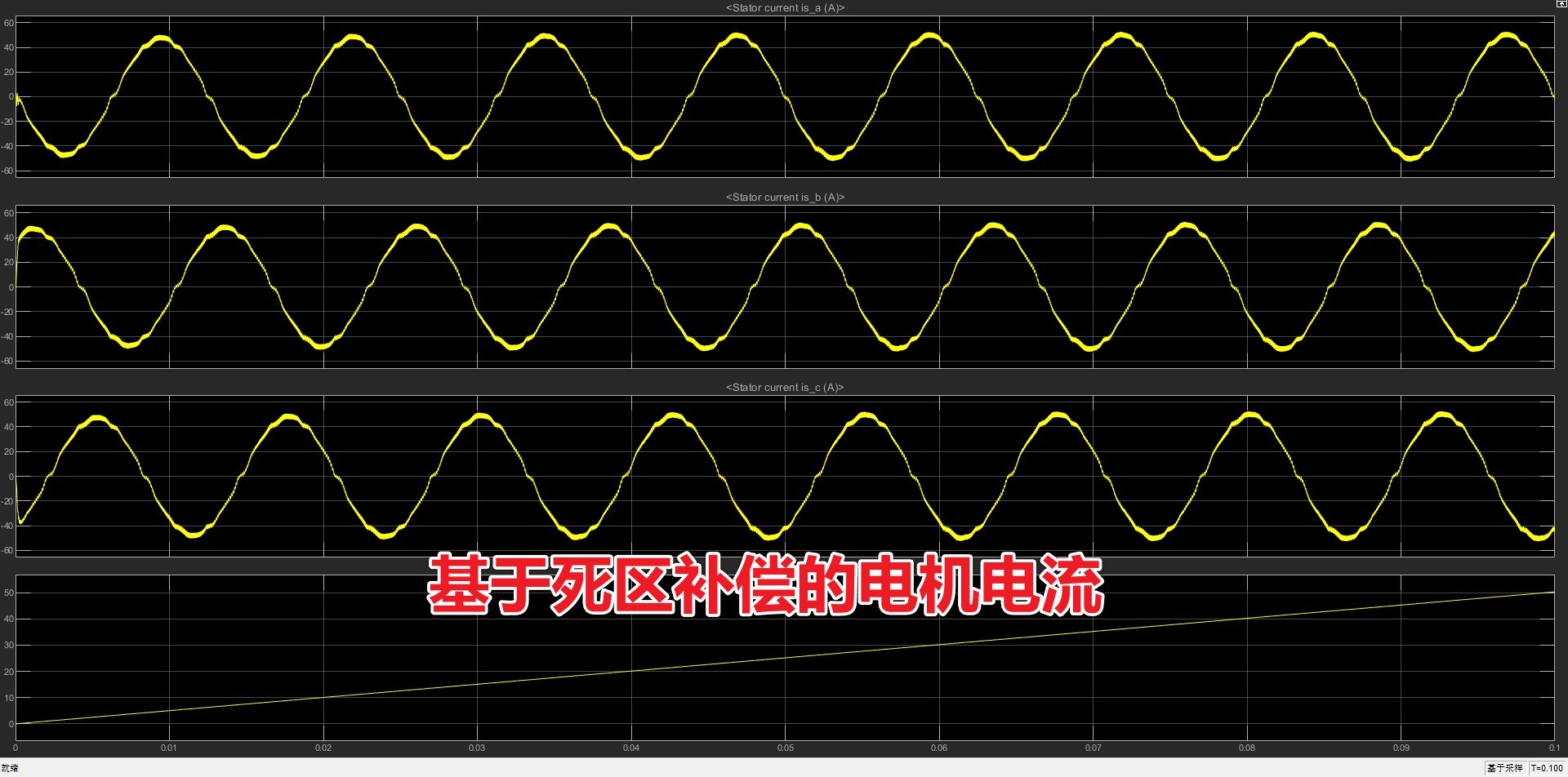
为了更直观地了解死区补偿的效果，我们搭建了两套系统进行仿真。一套是使用死区补偿的PMSM矢量控制系统，另一套则是未使用死区补偿的系统。这就像一场对比实验，能让我们清晰地看到死区补偿前后的差异。

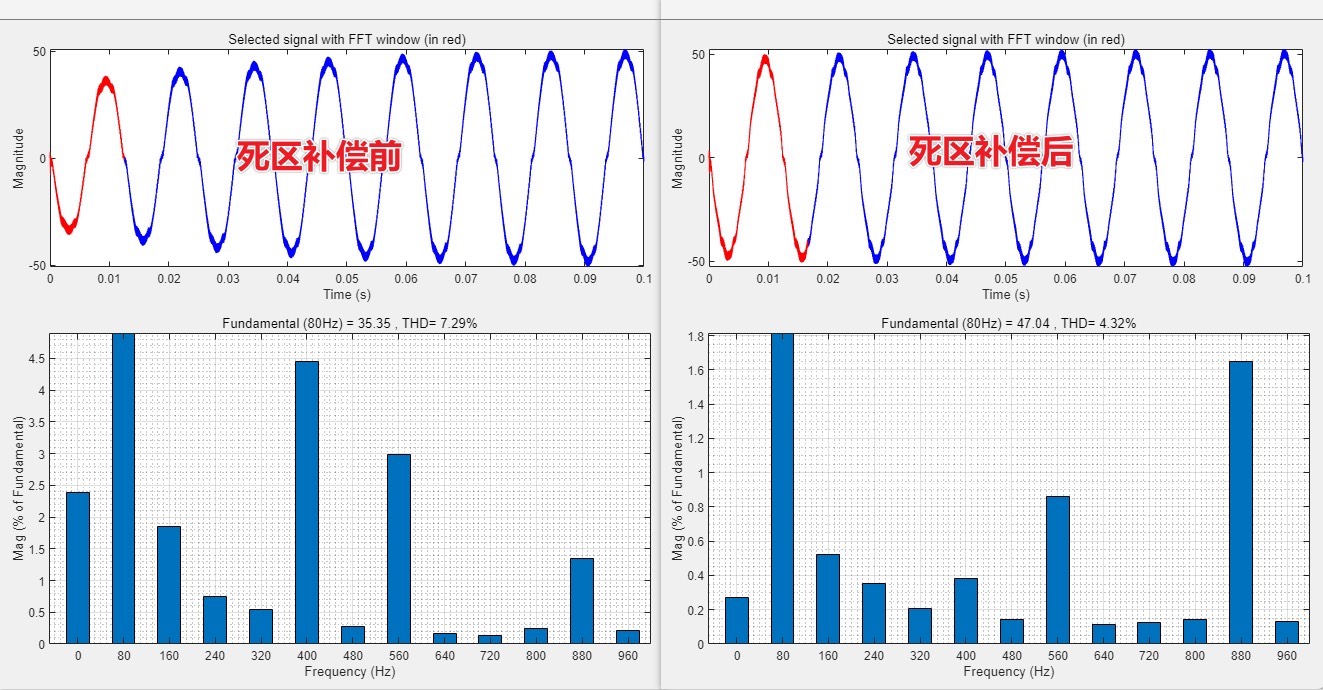
接下来，重点讲讲死区补偿的实现方式。这里采用了电流检测、判断角度逻辑，进而输出补偿角的方法。下面简单写一段伪代码来示意这个过程（以Python为例，只是示意逻辑，非实际运行代码）：

# 假设这里获取到了电流值
current_value = get_current() 
# 这里假设获取到了角度值
angle_value = get_angle() 

# 根据电流值和角度值判断是否需要补偿
if current_value > certain_threshold and (angle_value > angle_threshold1 and angle_value < angle_threshold2): 
    compensation_angle = calculate_compensation_angle(current_value, angle_value) 
    # 输出补偿角，在实际中这可能会影响PWM信号的生成
    output_compensation_angle(compensation_angle) 

在这段代码里，首先获取电流值和角度值，这两个值是判断是否需要进行死区补偿的重要依据。然后通过条件判断，如果电流值超过某个设定的阈值，并且角度值在特定范围内，就说明需要进行补偿。接着调用 calculatecompensationangle 函数来计算补偿角，最后通过 outputcompensationangle 函数输出补偿角，这个补偿角会在实际应用中影响PWM信号的生成，从而实现死区补偿。

对于正在学习相关内容的同学，强烈建议结合这个仿真以及相关文献一起研究。因为仿真能够让你直观地看到死区补偿前后电机运行状态的变化，而文献则能从理论层面为你深入剖析背后的原理，两者相辅相成，能让你对基于死区补偿的永磁同步电机SVPWM控制有更全面、更深入的理解。

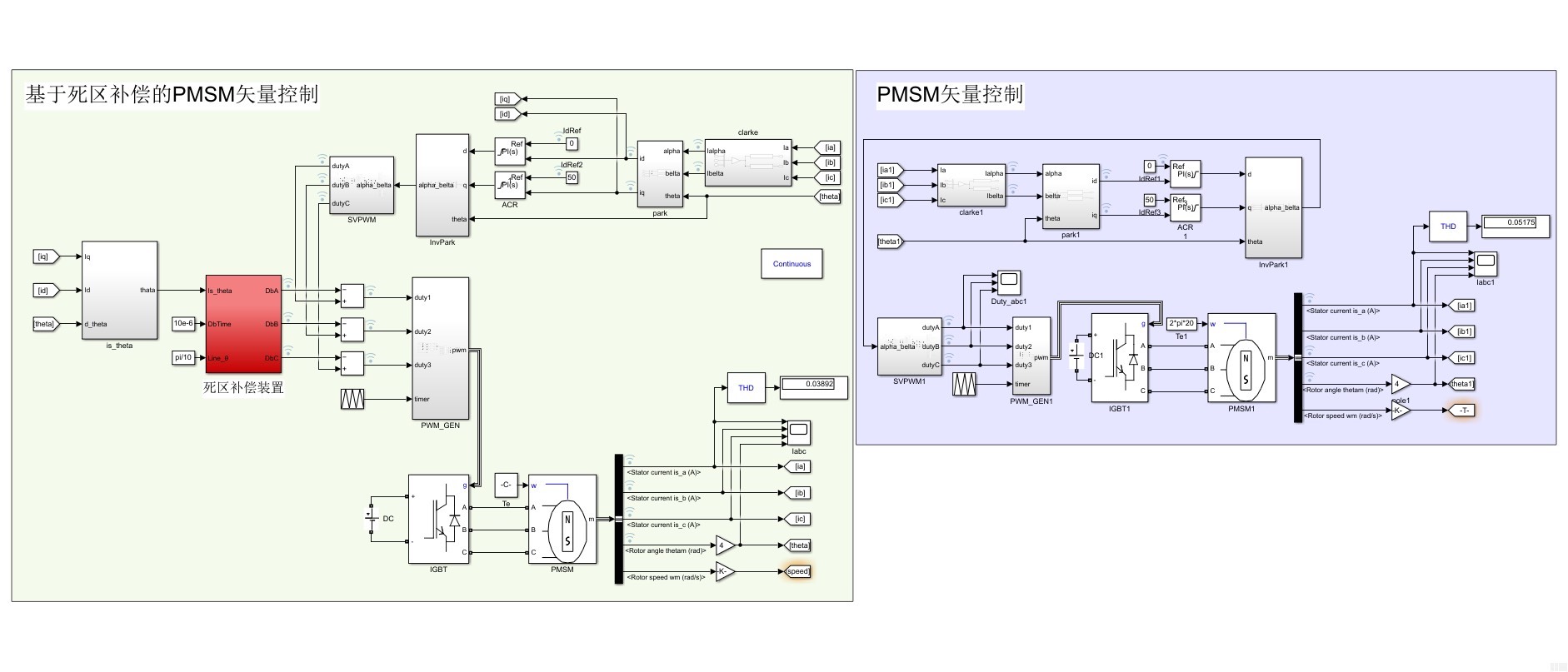
最后，给大家分享全套资料。其中包括完整仿真模型，这个模型就像是一个宝藏箱，打开它你可以详细了解每一个环节的设置和运行逻辑；还有相关参考文献，这些文献是前人智慧的结晶，能为你提供不同角度的思考和研究方向。希望大家在探索这个领域的过程中，能够借助这些资料，收获满满，在永磁同步电机控制的道路上越走越远。