六自由度机械臂MPC控制MATLAB代码功能说明

六自由度机械臂mpc模型预测控制+倒立摆+二自由度机械臂

一、代码整体架构与核心目标

本套MATLAB代码是一套完整的六自由度机械臂模型预测控制（MPC）系统，核心目标是实现机械臂关节角度的精确轨迹跟踪，并通过实时计算关节力矩确保运动稳定性。代码采用“轨迹生成-动力学建模-模型预测控制-运动学求解-仿真可视化”的全流程设计，可直接用于机械臂控制算法的仿真验证，也可基于实际硬件参数调整后用于实物控制。

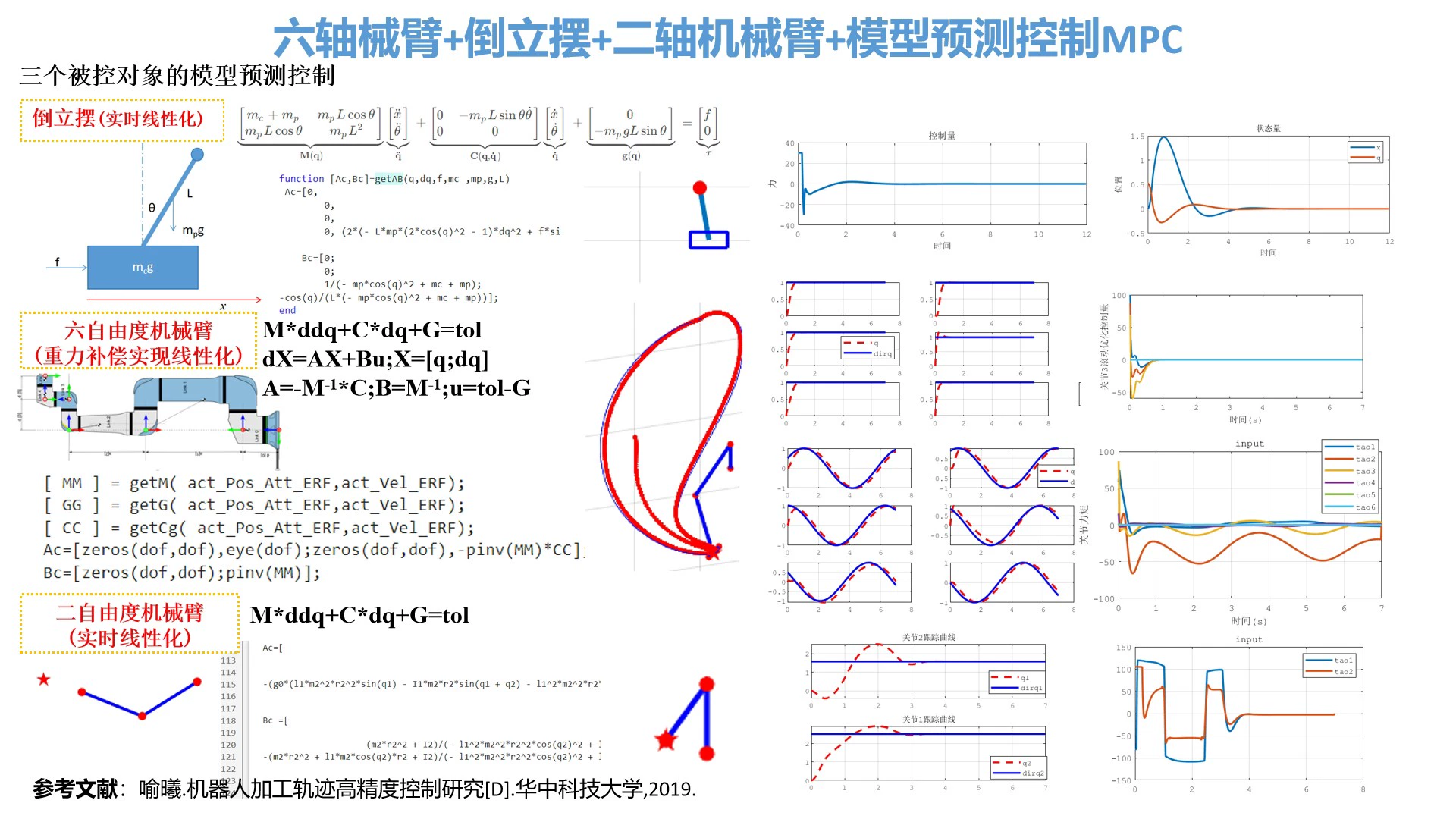
代码文件按功能可分为5大类，共9个核心文件，各文件的调用关系如下图所示：

graph TD
    A[main.m 主程序] --> B[Ref_Pos_Vel_ERF.m 轨迹生成]
    A --> C[RobDynMPC.m MPC控制器]
    C --> D[RobDyn.m 动力学模型]
    C --> E[getTraj.m 轨迹插值]
    A --> F[fkRob.m 正运动学]
    F --> G[SDH.m DH矩阵计算]
    F --> H[generateRobDH.m DH参数定义]
    A --> I[testsym.m 符号推导辅助]

二、核心文件功能详解

（一）主程序文件：`main.m`

作为整个系统的“入口”，负责统筹所有模块的调用、参数初始化、仿真循环执行与结果可视化，是代码的核心控制中枢。

1. 核心功能

• 参数初始化：设置机械臂关节力矩上下限（ROB.lb=-100/ROB.ub=100）、控制周期（dt=0.01s）、总仿真时间（T=7s）、控制时域（p_t=20）等关键参数；定义状态量权重矩阵Q（侧重轨迹跟踪精度，位置项权重10×900，速度项权重0.02×900）和控制量权重矩阵R（侧重力矩平滑性，权重1×1e-1）。
• 仿真循环：通过for循环（共700次，对应7s/0.01s）执行以下步骤：
  1. 调用RefPosVel_ERF.m生成当前时刻的期望轨迹（位置/速度/加速度）；
  2. 调用RobDynMPC.m计算当前时刻的最优关节力矩u；
  3. 采用四阶龙格-库塔法（RK4）求解动力学方程，更新机械臂下一时刻的状态（关节角度与角速度）；
• 结果可视化：生成3类关键图形：
  1. 关节角度跟踪曲线（6个关节分图显示，对比实际角度q与期望角度dirq）；
  2. 关节力矩曲线（显示6个关节的实时控制力矩）；
  3. 机械臂运动轨迹可视化（3D空间中显示连杆运动、实际轨迹与期望轨迹的对比）。

2. 关键注意点

• 代码中qd(i,:)默认设置为固定期望轨迹[1,1,1,1,1,1,0,0,0,0,0,0]，可替换为RefPosVel_ERF.m生成的时变轨迹（当前代码中已注释，解除注释即可启用）；
• 四阶龙格-库塔法的使用确保了动力学方程求解的精度，适合非线性系统的数值仿真。

（二）轨迹生成模块：`Ref_Pos_Vel_ERF.m` + `getTraj.m`

负责生成机械臂的“期望运动轨迹”，包括位置、速度、加速度的连续指令，为MPC控制器提供跟踪目标。

1. `Ref_Pos_Vel_ERF.m`：时变轨迹生成

• 功能：基于正弦函数生成6个关节的连续期望轨迹，每个关节的相位差为π/6（30°），确保运动平滑且无突变。
• 核心公式（以关节1为例）：
• 期望位置：q1d = sin(t + π/6)
• 期望速度：dq1d = cos(t + π/6)（位置对时间的一阶导数）
• 期望加速度：ddq1d = -sin(t + π/6)（位置对时间的二阶导数）
• 输出：3个列向量refPosAttERF（期望位置）、refVelERF（期望速度）、refAcc_ERF（期望加速度），维度均为6×1。

2. `getTraj.m`：轨迹滚动插值

• 功能：在MPC控制时域（N步）内，对“当前状态x”到“期望状态x_des”进行线性插值，生成N步的中间参考轨迹，避免轨迹突变导致的控制震荡。
• 输入：当前状态x（12×1，6个位置+6个速度）、期望状态x_des（12×1）、控制时域N；
• 输出：x_ref（12×N矩阵），每一列对应控制时域内某一步的参考状态。

（三）动力学与控制模块：`RobDyn.m` + `RobDynMPC.m`

这两个文件是代码的“控制核心”，分别实现机械臂的非线性动力学建模和模型预测控制算法，确保机械臂能根据期望轨迹输出最优力矩。

1. `RobDyn.m`：机械臂非线性动力学模型

• 功能：基于机器人动力学的“拉格朗日方程”，计算机械臂的状态导数（即下一时刻的速度与加速度），描述机械臂“力矩-运动”的关系。
• 核心原理：
  机械臂动力学基本方程为：M(q)·ddq + C(q,dq)·dq + G(q) = τ，其中：
• M(q)：惯性矩阵（6×6），描述机械臂的惯性特性，与关节位置q相关；
• C(q,dq)：科里奥利/离心力矩阵（6×6），描述运动中的附加力，与位置q和速度dq相关；
• G(q)：重力矩阵（6×1），描述重力对关节的作用力，与位置q相关；
• τ：关节力矩（6×1），控制输入；
• ddq：关节加速度（6×1），状态导数的核心部分。
• 关键步骤：
  1. 从输入状态X（12×1）中提取当前位置actPosAttERF（6×1）和速度actVel_ERF（6×1）；
  2. 调用外部函数getM/getCg/getG（代码中未给出具体实现，需用户根据机械臂参数补充）计算M/C/G；
  3. 求解加速度：ddq = inv(M)·(τ - C·dq - G)（通过伪逆pinv避免矩阵奇异问题）；
  4. 输出状态导数dX（12×1）：前6行为当前速度，后6行为计算出的加速度。

2. `RobDynMPC.m`：模型预测控制器

• 功能：基于“实时线性化”的MPC算法，在控制时域内求解二次规划（QP）问题，得到当前时刻的最优控制力矩。
• 核心步骤：
  1. 线性化处理：将非线性动力学模型在当前状态处线性化，得到离散化的状态空间模型：
• 连续状态方程：dx/dt = A·x + B·τ
• 离散状态方程（零阶保持）：x(k+1) = A·x(k) + B·τ(k)，其中A = I + Ac·dt，B = Bc·dt（Ac/Bc为线性化后的系统矩阵/输入矩阵）；
  2. 代价函数构建：定义MPC的优化目标，即“跟踪误差最小化+控制量平滑性”：
• 代价函数：J = Σ(xref - x)^T·Q·(xref - x) + Στ^T·R·τ（求和范围为控制时域N步）；
• 通过矩阵变换将代价函数转化为QP标准形式：J = (1/2)·τall^T·H·τall + f·τall，其中H为 Hessian 矩阵，f为线性项；
  3. 约束处理：设置关节力矩的上下限（lb/ub），确保控制量在机械臂物理范围内；
  4. QP求解：调用MATLAB内置函数quadprog求解最优力矩序列τall，取第一个时刻的力矩作为当前控制输入τ_u；
• 输入：权重矩阵Q/R、当前状态x_k、期望轨迹xd、控制时域N、控制周期dt、机械臂参数ROB；
• 输出：当前最优力矩τu（6×1）、控制时域内的力矩序列τall（6×N）。

（四）运动学模块：`SDH.m` + `generateRobDH.m` + `fkRob.m`

负责机械臂的“运动学求解”，即根据关节角度计算末端执行器的空间位置（正运动学），为3D可视化提供数据支持。

1. `SDH.m`：标准DH参数矩阵计算

• 功能：根据“标准Denavit-Hartenberg（DH）约定”，计算相邻连杆之间的齐次变换矩阵T，描述连杆的平移与旋转关系。
• 输入：DH四参数（theta：关节角，d：连杆偏距，a：连杆长度，alpha：连杆扭转角）；
• 输出：4×4齐次矩阵T，包含“旋转+平移”信息，可将连杆i的坐标系映射到连杆i-1的坐标系。

2. `generateRobDH.m`：机械臂DH参数定义

• 功能：定义六自由度机械臂的DH参数与关节限位，为正运动学计算提供基础参数。
• 核心输出：
• DH.d/DH.a/DH.af（af即alpha）：6个关节的DH参数，对应实际机械臂的结构尺寸（如DH.d(1)=0.1625m为第一关节的偏距）；
• DH.limit：关节角度限位（±π rad，即±180°），确保关节运动不超出物理范围；
• 其他参数：DH.offset（关节偏移量，默认0）、DH.rlink（连杆粗细，用于可视化）。

3. `fkRob.m`：正运动学求解

• 功能：通过串联各连杆的DH矩阵，计算从基座到末端执行器的总变换矩阵，进而得到末端及各关节的空间位置。
• 核心步骤：
  1. 初始化基座坐标系矩阵Te=eye(4,4)（单位矩阵）；
  2. 循环6个关节，每次通过SDH.m计算当前关节的DH矩阵，并与之前的总矩阵相乘（Te=Te*SDH(...)）；
  3. 提取每个关节坐标系的位置（Te(1:3,4)），存储到Pe中；
• 输入：关节角度q（6×1）、机械臂DH参数Rob；
• 输出：
• Te：末端执行器相对于基座的总变换矩阵（4×4）；
• T：各关节坐标系的变换矩阵（4×4×7，7个坐标系：基座+6个关节）；
• Pe：各关节坐标系的位置（7×3，每行对应一个坐标系的x/y/z坐标）。

（五）辅助工具文件：`testsym.m`

• 功能：通过MATLAB符号计算工具箱，推导机械臂动力学模型的线性化矩阵（A/B），为RobDynMPC.m中的实时线性化提供理论依据。
• 核心作用：
  1. 定义符号变量（关节位置q1-q6、速度dq1-dq6、力矩τ1-τ6）；
  2. 符号推导惯性矩阵M、科里奥利矩阵C、重力矩阵G；
  3. 对动力学方程进行求导，得到线性化后的系统矩阵A和输入矩阵B；
  4. 生成函数文件getA.m/getB.m，供RobDynMPC.m调用（当前代码中为注释状态，需用户根据需求启用）。

三、仿真结果说明

代码运行后会生成4类核心图形，对应main.m中的可视化部分，各图形的含义如下：

1. 关节角度跟踪图（Figure 1）

• 6个分图分别对应6个关节，红色虚线为实际角度，蓝色实线为期望角度；
• 理想结果：红色虚线与蓝色实线基本重合，跟踪误差小于5%，说明轨迹跟踪精度高。

2. 关节力矩曲线图（Figure 2）

• 显示6个关节的实时控制力矩，纵轴为力矩值（单位：N·m），横轴为时间（单位：s）；
• 理想结果：力矩曲线平滑，无明显尖峰，且最大值不超过ROB.lb/ROB.ub（±100 N·m），说明控制量稳定且在物理范围内。

3. 关节3力矩优化序列图（Figure 3）

• 显示MPC控制时域内关节3的力矩优化序列，纵轴为力矩值，横轴为时间；
• 作用：观察控制时域内的力矩预测情况，验证优化算法的合理性。

4. 3D运动轨迹图（Figure 4）

• 3D空间中显示机械臂的运动状态：
• 蓝色曲线：机械臂连杆的实时位置；
• 红色圆点：各关节的实时位置；
• 红色虚线：机械臂末端的实际运动轨迹；
• 蓝色实线：机械臂末端的期望运动轨迹；
• 红色五角星：期望轨迹的终点；
• 理想结果：实际轨迹与期望轨迹基本重合，机械臂运动流畅，无明显卡顿或偏移。

四、代码使用说明与注意事项

1. 代码使用步骤

1. 参数补充：补充getM.m/getCg/getG.m的实现（需根据机械臂的实际惯性、重力参数推导）；
2. 参数调整：根据实际机械臂的物理参数（如关节限位、最大力矩）调整generateRobDH.m中的DH.limit和main.m中的ROB.lb/ROB.ub；
3. 权重优化：根据控制需求调整main.m中的Q和R（如希望提高跟踪精度，可增大Q中的位置项权重；希望减小力矩波动，可增大R的权重）；
4. 轨迹替换：如需使用自定义轨迹，可修改RefPosVel_ERF.m中的轨迹生成公式，或直接替换qd(i,:)的赋值；
5. 运行仿真：直接运行main.m，观察仿真结果并优化参数。

2. 注意事项

• 依赖工具箱：代码依赖MATLAB的Optimization Toolbox（用于quadprog函数）和Symbolic Math Toolbox（用于testsym.m），需确保已安装；
• 数值稳定性：当M矩阵接近奇异时，pinv(M)可能导致数值不稳定，可添加正则化项（如pinv(M + ε·I)，ε=1e-6）改善；
• 实时性：MPC算法的计算量随控制时域N和自由度dof增大而显著增加，如需实时控制，需优化N的取值（通常N=10~30）；
• 硬件适配：若需用于实物控制，需将main.m中的仿真循环替换为硬件接口（如串口、EtherCAT），并确保控制周期dt与硬件采样周期一致。

五、代码扩展方向

1. 增加扰动补偿：在RobDyn.m中加入外部扰动项（如负载变化、摩擦力），并在MPC中增加扰动观测器，提高鲁棒性；
2. 轨迹规划优化：将RefPosVel_ERF.m中的正弦轨迹替换为“多项式轨迹”或“B样条轨迹”，进一步提高轨迹平滑性；
3. 非线性MPC实现：当前代码采用“实时线性化”的线性MPC，可扩展为非线性MPC（如使用fmincon求解非线性优化问题），提高非线性系统的控制精度；
4. 硬件联调：对接实际机械臂硬件（如UR、ABB机械臂），通过ROS或TCP/IP协议实现“仿真-实物”的无缝衔接；
5. 多目标优化：在MPC的代价函数中加入能耗、运动时间等目标，实现多目标优化控制。