隐私保护压缩感知交通监控

面向城市实时交通监控的隐私保护压缩感知

摘要

交通监控是通过在城市道路网络中收集车辆数据来解决交通问题的重要手段。然而，敏感数据的泄露增加了攻击者窥探驾驶员隐私的风险。为了在不泄露数据隐私的前提下实现实时交通监控，我们提出了一种隐私保护压缩感知（PPCS）机制，以及时获取整个道路网络的交通状况，并设计了一系列可行且安全的计算协议以加快数据处理速度。具体而言，我们利用云提取不同道路路段之间的时空相关性，并计算少量道路路段的交通拥堵率。值得注意的是，我们采用压缩感知（CS）技术，基于若干已知道路路段的值来估计其他未知路段的交通状况。此外，全面的安全分析表明，所提出的PPCS能够有效防止车辆数据泄露。最后，我们通过计算成本和通信开销的模拟实验验证了该机制的有效性和效率。

索引词 —云平台，压缩感知，隐私保护，安全两方计算，交通监控。

一、引言

近年来，智慧城市的建设引起了广泛关注。作为构建智慧城市的核心，掌握道路交通状况有助于实现智能交通系统，并帮助主管部门调度交通信号时间[1]。交通拥堵是反映道路不同状况的最重要指标之一，与车辆的时间和燃油消耗密切相关。此外，它还大大增加了交通事故的可能性，进一步对人们的生命和财产造成严重威胁[2]。因此，实时了解道路交通状况以避免交通堵塞至关重要。

传统交通监控方法基于静态传感器，例如闭路摄像机和感应线圈检测器。由于静态传感器的部署和维护成本较高，传统方法难以大规模采用[3],[4]。随着车载传感器性能的不断提升，许多公司利用收集的车辆数据来分析和预测交通状况，例如谷歌或百度地图[5]。然而，车辆生成的数据量巨大，这对数据存储和处理提出了新的要求。因此，我们将依赖一种不仅能够提供足够数据存储，而且具有强大数据处理能力的设备。

如今，分布式云的提出极大地丰富了云的使用，使得云服务提供商能够按需租用基础设施，并从通信服务提供商处获取专用资源[6],[7]。此外，该基础设施涵盖从路由器和链路到服务器和数据库的广泛范围。更重要的是，与当前的云相比，分布式云还利用地理多样性来存储具有相同特征的数据，以实现安全的数据处理。借助分布式云，可以有效解决数据存储和处理的问题[8],[9]。然而，当云执行数据处理时，外包数据的隐私常常会泄露。因此，主要挑战在于确保外包数据不被未经授权地披露。

为了实现交通监控，车辆数据被外包到云中并进一步分析[10],[11]。然而，这些数据包含一些敏感信息，例如GPS位置、上报时间和速度等。例如，如果攻击者截获了某车辆连续的速度和GPS位置观测数据，则可通过挖掘技术预测驾驶员的行驶路线。此外，GPS信息还会暴露驾驶员常去的地点，如家、办公室和餐馆。另外，通过比较起始位置和速度表收集的数据，还可以预测驾驶员的目的地[12]。因此，保护数据隐私至关重要。目前已有一些数据加密算法，例如同态加密（HE）算法[13]和安全多方计算（MPC）[14]。然而，即使存储在云中的数据已加密，我们仍面临一项研究挑战：如何在不损害数据隐私的前提下加速这些关键的算术运算。此外，随着城市中道路数量急剧增加，短时间内从所有道路收集车辆数据变得极为困难，实现实时交通监控几乎不可能。因此，有必要实现基于少量数据实现对整个道路网络的实时交通监控目标。

受上述挑战的启发，我们提出了一种隐私保护压缩感知（PPCS）机制，以实现获取每条道路交通拥堵状况的实时交通监控。该机制利用多方计算（MPC）实现安全数据处理，并采用压缩感知（CS）技术完成对未知值的估计。

我们的贡献总结如下。

• 我们构建了一个交通监控模型，用于收集车辆数据。在该模型下，我们考虑一种新的数据收集模式，即车辆将自身的驾驶报告上传至路侧单元（RSU）。随后，RSU将整合上报的记录，以计算道路路段的平均速度和特征值。最终，这些数据处理结果将被发送至云平台（CP），并在CP中执行一些复杂的计算。
• 我们提出了一种PPCS机制，通过分析部分道路路段的交通拥堵率，实现对整个道路网络的实时交通监控。然后，我们利用多方计算（MPC）来确保数据处理过程中的隐私安全。为了加快数据处理速度，我们基于MPC设计了多个安全计算协议。
• 我们提取特定时间区间内道路网络的时空相关矩阵，以挖掘不同时段的历史数据，同时不泄露数据隐私。为实现实时交通监控，我们采用压缩感知技术，基于一些已知值快速估计道路网络的交通拥堵率。
• 我们形式化地证明了PPCS机制的安全性和隐私性，并评估了其计算成本和通信开销。此外，我们还在不同数量的已知道路路段情况下对PPCS进行了实验验证。

本文的其余部分组织如下。我们在第二节介绍相关工作。在第三节中，介绍了作为一些基础知识的预备知识。接着，在第四节中给出了系统模型、安全威胁以及设计目标的形式。在第五节中，我们详细描述了实现交通监控的PPCS机制。接下来，在第六节中还分析了机制安全性，并给出了PPCS性能。最后，在第七节中对本文进行总结。

II. 相关工作

最近，交通监控受到了广泛关注，有助于减少空气污染和交通事故，从而改善驾驶体验。关于交通监控已有许多研究工作[15]–[19]。Yoon et al.[15]提出了一种识别交通状况的简单有效方法，该方法需要上报GPS位置数据。Zhou et al.[16]引入了一种基于乘客参与式感知的公交到站时间预测系统。为了降低交通估计的成本，Zhu et al.[17]提出了一种基于压缩感知和探测车辆的城市交通估计方法，该方法不依赖复杂的交通模型即可实现城市中的交通估计。此外，Liu et al.[18]挖掘了道路网络基于交通数据的相关性实现交通估计。Frank et al.[19]提出采用不同的机器学习算法对交通状况进行推断。然而，上述研究未考虑交通监控中潜在的数据泄露风险。这些现有方法需要利用大量数据，而未考虑数据隐私问题。随着人们安全意识的提升，许多研究人员开始意识到应在不泄露任何信息的前提下进行交通监控[20], [21]。

如果用户数据得不到保护，驾驶员通常不愿意提交其数据，并进一步防止第三方服务提供商从中获利。更重要的是，交通监控旨在获取道路的交通状况，同时需要满足实时特性。

实际上，已有一些方法被提出以实现无数据泄露的交通监控。例如，Zhao et al.[22]提出了一种针对基于物联网的智慧城市中的最优边缘资源分配方法，以确保边缘数据的安全。随后，Chim et al.[23]提出了一种利用RUS在分布式方式下引导车辆的安全导航方案。然而，所有车辆均接收到相同的主密钥来解密其他车辆的数据，这无法防止内部攻击。为避免上述问题，Zhu et al.[24]提出了一种匿名轨迹的隐私漏洞揭示方法，该方法通过引入一种新的去匿名化攻击范式，从匿名轨迹数据集中重新识别受害者的轨迹，从而保护配备GPS轨迹的移动设备的隐私。此外，Sur et al.[25]设计了一种基于车载云的安全导航系统，并从内部威胁和数据泄露点的角度提供了更可靠的导航服务概念。Ni et al.[26]和Wang et al.[27]提出了一种基于雾计算的车载自组织网络中利用车载空间众包实现的实时导航安全且隐私保护的导航方案。然而，上述方法中的数据保护策略效率非常低下。此外，Rabieh et al.[28]提出了一种隐私保护的路线报告方案。在其系统中，收集车辆的历史路线以计算出现在后续路线中的车辆数量。此外，还提出了诸如椭圆曲线密码学[29]和密钥聚合等密码学原语来保护数据隐私[30]，但这可能会给车辆带来较大的计算负担。Baik et al.[31]提出了一种基于虚拟行程线和相关伪装技术的分布式隐私保护系统，该系统利用配备全球定位系统的探测车辆实现了汽车交通监控。Belal et al.[32]采用隐私保护协作的方式，通过两种不同方法进行交通监控，并设计了一种隐私保护的位置更新机制，以满足交通监控和地图生成的需求。在[33], Hui et al.中，提出了通过混淆时间准则来刻画位置数据集中的隐私，实现GPS轨迹中的隐私保护。He et al.[34]提出了一种隐私保护上传机制，通过多目标优化问题满足用户多样化的隐私需求。一种基于同态Paillier密码系统的隐私保护交通监控方案在[20]中被提出。Mentari et al.[35]描述了一种通过关联被动测量帮助诊断网络中断的系统。

以隐私保护的方式从多个互联网服务提供商（ISPs）获取数据。此外，他们还提出了一种高效的多方计算多次（MPC）协议，以大幅加速MPC比较操作。上述大多数方法主要考虑了车辆数据的隐私，并利用同态加密实现交通监控。然而，使用同态加密保护数据隐私耗时较长，会违反实时交通监控的实时性要求。受文献[36],[37],工作的启发，我们应用基于压缩感知技术的两方安全计算，以减少数据量并实现对整个道路网络的实时交通监控。尽管许多现有方法能够实现无数据泄露的交通监控，但它们忽略了路网的数据传输量和时间特征。数据加密是一项耗时的任务，因此设计一种适用于基于隐私保护的车载数据进行交通监控的加密机制至关重要。

III. 预备知识

在本节中，我们给出一些基本的预备知识、路网拓扑结构以及交通监控的目标。

A. 安全两方计算

安全两方计算模型被引入以通过联合计算[38]实现预期功能，同时不泄露各自的私有数据。假设有两个独立的个体Alice和Bob，他们分别存储自己的数据。例如，Alice有一个数a，Bob有一个数b，目标是获得乘法结果a·b，并将中间结果拆分为两个新值，重新分配给Alice和Bob。假设F定义了所需的计算模式，则经过k−1次计算后可得到最终结果Sk ← Fk(Ak−1, Bk−1)。然后，中间结果Sk被随机划分为相等部分，例如Ak + Bk = Sk。最后，Alice知道Sk，Bob知道Bk，如图1所示。

所引入的安全两方模型能够有效保护各方的输入数据，同时完成预期函数的计算，并且可以提高数据处理的有效性。

B. 压缩感知理论

对于高频信号，传统采样方法需要满足奈奎斯特定理，即采样频率至少为原始信号频率的两倍。然而，现有的硬件设备类型难以达到传统采样方法所需的频率。

为了解决这一问题，压缩感知（CS）技术是一种用于降低信号维度的新方法。与奈奎斯特采样定理相比，压缩感知（CS）能够以更低频率实现对原始信号的恢复。假设存在一个向量x=(x1, x2,…, xn)T，如果该向量x最多有k(k << n)个非零元素，则称x为一个k‐稀疏信号。

为了降低x的维度，应用一个测量矩阵Φ ∈ Rm×n以获得一个m维信号y ∈ Rm×1。当然，压缩感知理论要求测量矩阵Φ满足限制等距性质（RIP），例如高斯或伯努利随机矩阵。压缩感知理论指出，k‐稀疏信号x可以通过求解一个ℓ1‐最小化问题，以高概率从m= O(klog(n/k))个测量值的线性组合y中准确恢复。

$$
\min_{x \in \mathbb{R}^n} |x|_1 \quad \text{s.t.} \quad y = \Phi x. \tag{1}
$$

然而，自然界中存在的信号（如温度和湿度）并非完全k稀疏，因为它们可能具有k个较大的变换系数。假设信号x可以表示为Ψ=(ψ1, ψ2,…, ψn)

$$
x = \Psi \theta = \sum_{i=1}^{n} \theta_i \psi_i. \tag{2}
$$

在正交基n×nΨ中，其中θ=(θ1, θ2,…, θn)T是x在基Ψ下的变换系数。

C. 交通拥堵率

交通监控旨在让驾驶员掌握道路拥堵率，以选择更好的行驶路线。变量ci表示交通拥堵率，其计算公式如下。

$$
c_i = \frac{1}{v_i}. \tag{3}
$$

其中vi表示道路路段的平均速度，i用于标识不同的道路路段。

为了研究交通监控，通常需要利用图的知识来辅助通过已知值估计未知道路的交通拥堵率。假设图G(o, h, p)为路网的拓扑结构。o表示节点的数据集，在G中，h表示任意节点之间连接线的数据集，而p是一个变量值，用于反映不同道路路段之间的时空相关性强度，提取关键数据特征，并进一步在确定的时间间隔内去除冗余数据。相较于实际路网，o和h分别对应道路网络中的交叉口和道路路段。此处，图2可以更清晰地理解拓扑结构与实际路网之间的映射关系。

IV. 问题描述

在本节中，我们将阐述我们的系统模型、安全威胁和设计目标。

A. 系统模型

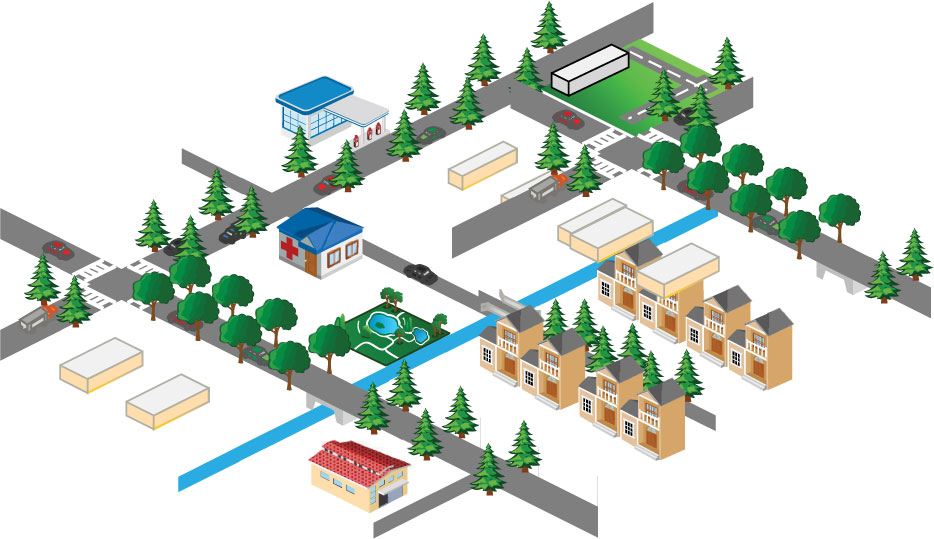
类似于许多安全外包数据模型，用于交通监控的PPCS采用诚实但好奇模型（HBC）[39],[42]。本文中，安全两方计算作为多方计算（MPC）的一个分支，用于构建一个包含五个实体的系统模型：第三方服务提供商（TPS）、云平台A和B（CPA/CPB）、路侧单元（RSU）、数据车辆（DVs）以及导航服务提供商（NSP），如图3所示。

• TPS是一个不可或缺且完全可信的参与方，负责生成涉及的必要随机数。随后，TPS通过安全通信信道分别将随机数发送给DV、CPA、CPB和NSP。
• CPA和CPB是诚实但好奇的参与方，提供无限的数据存储空间，并存储外包的车辆数据。此外，CPA和CPB具备强大的计算能力，能够执行安全加密协议以隐藏数据。
• RSU作为接入点的角色，在城市中广泛部署，也具备一定的存储与计算能力。更重要的是，根据数据属性，RSU将来自同一道路路段的数据集中存储。由于RSU的能力有限，它仅负责完成简单数据处理，并将处理结果安全地传输给CP。
• DVs是生成车辆数据的车辆，这些数据包括瞬时速度、时间、GPS位置等，随后这些数据被外包至RSU。
• NSP首先从云接收密文，然后基于少量已知的交通拥堵状况，估计未知道路的交通拥堵状况。最后，NSP将整个道路网络的交通拥堵状况发送给DV。

B. 安全威胁

安全威胁来自交通监控系统中的两个攻击方面。

根据本文中交通监控的特点，TPS是一个不可或缺且完全可信方。然而，CPA/CPB和RSU是诚实但好奇的，它们严格遵守协议，但有兴趣获取属于挑战方CP和RSU的数据。在此，我们在模型中引入三个主动攻击者A1、A2和A3。A1的目标是拦截所有公共通信链路以获取传输中的加密数据，而A2的目的是攻击RSU、CPA/CPB并解密密文。A3具备A1和A2的能力，可以攻击整个模型。因此，A1和A2均具备以下能力：

1. A1可以窃听公共通信链路以推断密文的明文值。
2. A2可以猜测由路侧单元和计算方加密的密文的明文值。

C. 设计目标

为了在上述系统模型下实现所提出的机制并抵御安全威胁，我们的机制应达到以下设计目标。

• 数据安全 ：外包数据的传输和存储应是安全的。任何攻击者都无法通过截获加密数据来推断真实数据，且数据处理过程是安全的。攻击者无法通过挖掘历史数据来推测数据隐私。更重要的是，交互计算的中间结果不会泄露任何私有信息。
• 数据处理速度 ：由于计算涉及大量数据，数据处理的计算应轻量高效，并且数据处理结果应准确。
• 交通监控的实时性 ：为了提升用户的驾驶体验，交通监控应快速且低延迟。估计的交通拥堵率应及时通知驾驶员。

五、系统框架

在本节中，我们主要阐述实现用于交通监控的PPCS的更多细节。我们提出了车辆数据传输的形式，并建立了系统框架。

A. 系统概述

如图4所示，我们可以看到PPCS包含四个阶段，即车辆数据生成、安全数据收集、安全数据处理和安全数据估计。以下是对这些阶段的简要概述。

• 车辆数据生成 。车辆作为PPCS中的主要参与者，生成数据并安全地持续将其发送到路侧单元。根据数据生成时间的长短，PPCS将其分为两类。

通常，一类包括前一小时内来自整个道路网络的数据，这些历史数据用于挖掘道路的时空相关性；另一类包含来自若干道路路段的数据，用于从特定时刻t开始监控接下来T′时间间隔内的交通状况。最终，我们实现了在T(T′< T)时间间隔内对整个道路网络的实时交通监控。

• 安全数据收集 。生成的车辆数据始终包含上报时间t ∈ Q+、瞬时速度v ∈ Q+、经纬度信息（lat ∈ Q+, lon ∈ Q+）、车辆身份id ∈ Q+以及车辆牌照号码lic ∈ Q+，这些可构成一个元组Q=[t, v, lat, lon, id, lic]。为保护数据隐私，数据收集的第一步是将元组Q中的每个元素随机分割为两部分，并分别发送到不同的RSU（路侧单元）。即，t被随机划分为t1和t2，例如t= t1+ t2；v也被随机分割为两部分v1和v2，例如v= v1+ v2；类似地处理lat= lat1+ lat2、lon= lon1+ lon2。然后将(t1, v1, lat1, lon1, id1, lic1)作为一组发送到一个RSU，(t2, v2, lat2, lon2, id2, lic2)也作为另一组发送到另一个RSU。完成第一步后，每个RSU对接收到的数据进行初步计算以获得中间结果。最后，各RSU还将每个中间结果随机分割为两部分，分别发送给CPA和CPB。

• 安全数据处理 。当路侧单元和云平台接收到数据后，它们将执行一系列安全数据处理。为了提高数据处理效率，安全数据处理也通过两步计算完成。首先，在路侧单元对数据进行初步计算，以获得参与一些复杂计算的综合数据。其次，由云执行一些复杂数据处理。与路侧单元中的数据处理模式不同，数据通过CPA和CPB之间的交互模式进行计算，以在不泄露中间结果的情况下获得道路拥堵率和时空相关矩阵。

• 安全数据估计 。PPCS可以通过少量已知交通拥堵率来估算整个道路网络。为了估计未知道路路段的交通状况，引入压缩感知技术参与未知值的估算。即，NSP接收

来自CPA和CPB的少数已知道路路段的交通拥堵率。然后，根据不同的稀疏度γ（γ表示已知道路路段占全部道路路段数量的百分比），NSP通过压缩感知的恢复算法估算未知道路的交通拥堵率，且不泄露私密信息。

为了更清晰地展示所提出系统的实施过程，图4给出了流程图。

B. 数据收集策略

假设所有参与的车辆都是诚实的，无需验证其身份。我们利用元组Q中的部分车辆数据（如u=[t, v, lat, lon]）来描述单条记录的隐私保护数据传输过程。具体而言，假设数据是在T时间间隔内收集的，在道路路段j中有m条移动信息记录，用于在T期间构建向量

$$
U_j = [u(j,1), u(j,2), …, u(j,m)]^T。
$$

此外，城市中有n个道路路段，每个道路路段在T期间都有上报数据，这些数据可组成矩阵M = [U1, U2, …, Un]。根据数据传输策略，矩阵M中的每个元素被随机分割为两部分，得到分量矩阵M′和M′′，例如M = M′ + M′′。然后将M′发送到一个附近的路侧单元（RSU），将M′′发送到另一个附近的路侧单元（RSU）。注意，我们利用路侧单元（RSU）在固定存储位置接收并进一步存储来自相同道路路段在T期间的数据。实际上，当路侧单元（RSU）接收到数据U时，它们会处理这些数据以获得某个路段的中间结果，例如u⊥ = [t⊥, v⊥, lat⊥, lon⊥]。为了提高数据处理效率，我们可以利用u⊥构成向量N，其中包含道路网络的位置结果。如前所述，城市中有n个道路路段，我们为不同道路路段分配从1到n的不同标签，以构建向量

$$
N = [u_{(⊥,1)}, u_{(⊥,2)}, …, u_{(⊥,n)}]。
$$

类似地，向量N被随机分割为两个分量向量N′和N′′，分别发送给CPA和CPB，以参与计算方（CP）中的交互计算。因此，向量N′和N′′可用作历史数据，以提取时空相关矩阵。假设我们在T′(T′< T)中对某些道路路段进行数据采集，CPA和CPB可以接收到两个分量向量N′o和N′′o，用于估计未知道路路段的交通拥堵率。

如图5所示，我们给出了一个简单且安全的数据收集示例，其中包含路段1、2和3。每个道路路段在T时间段内提供一些记录，箭头表示来自相应道路的数据组件，这些数据被发送到路侧单元和计算方中的相关数据存储单元©1, ©2, ©3。

C. 安全数据处理模式

为了获取交通拥堵ci以衡量交通状况，利用车辆数据计算道路平均速度v⊥和道路GPS位置信息（lat⊥, lon⊥）。然后，将计算任务分别分配给路侧单元和计算方。接下来，将详细说明数据处理的相关内容。

1) 路侧单元中的初步数据处理

路侧单元具有收集并完成一些初步计算的能力，并提取道路网络的一些重要特征。即，路侧单元计算道路平均速度v⊥和GPS位置信息(lat⊥, lon⊥)。为了获得v⊥和(lat⊥, lon⊥)，如上所述，在T′期间道路上的m上报的速度记录可以构造成一个向量V=[v1, v2, v3,…, vm]。然后，v⊥可以基于以下公式通过向量V计算得出。

$$
v_\perp = \frac{\sum_{i=1}^{m} v_i}{m}. \tag{4}
$$

根据公式(4)，假设有w(w< n)个已知道路路段，其平均速度构成一个向量V⊥=[v(⊥,1), v(⊥,2),…, v(⊥,w)]。然后，将V⊥随机分割为分量向量

$$
V’ \perp = [v’ {(\perp,1)}, v’ {(\perp,2)}, …, v’ {(\perp,w)}]
$$

和

$$
V’‘ \perp = [v’‘ {(\perp,1)}, v’‘ {(\perp,2)}, …, v’‘ {(\perp,w)}]。
$$

为了通过少量已知道路路段实现对整个道路网络实时交通状况的估计，采用压缩感知（CS）来估计未知路段的交通状况。值得注意的是，稀疏表示矩阵作为压缩感知中的基本因子，被构建用于提取道路网络的时空相关性。类似地，m是某道路路段在T期间上报的GPS位置数量，也可由纬度和经度组成两个向量，例如

$$
Lat = [lat_1, lat_2, lat_3, …, lat_m],
$$

$$
Lon = [lon_1, lon_2, lon_3, …, lon_m]。
$$

然后，时空特征值计算如下。

$$
lat_\perp = \frac{\sum_{i=1}^{m} lat_i}{m}. \tag{5}
$$

$$
lon_\perp = \frac{\sum_{i=1}^{m} lon_i}{m}. \tag{6}
$$

为了便于表述，假设每条道路路段报告m条记录，因此来自n条道路路段的所有记录可以构成矩阵M。

$$
M =
\begin{bmatrix}
u_{(1,1)} & u_{(2,1)} & \cdots & u_{(n,1)} \
u_{(1,2)} & u_{(2,2)} & \cdots & u_{(n,2)} \
\vdots & \vdots & \ddots & \vdots \
u_{(1,m)} & u_{(2,m)} & \cdots & u_{(n,m)}
\end{bmatrix} \tag{7}
$$

接下来，将M中的每个元素随机分为两部分，生成矩阵M′和M′′，例如

$$
M’ =
\begin{bmatrix}
u’ {(1,1)} & u’ {(2,1)} & \cdots & u’ {(n,1)} \
u’ {(1,2)} & u’ {(2,2)} & \cdots & u’ {(n,2)} \
\vdots & \vdots & \ddots & \vdots \
u’ {(1,m)} & u’ {(2,m)} & \cdots & u’_{(n,m)}
\end{bmatrix} \tag{8}
$$

$$
M’’ =
\begin{bmatrix}
u’‘ {(1,1)} & u’‘ {(2,1)} & \cdots & u’‘ {(n,1)} \
u’‘ {(1,2)} & u’‘ {(2,2)} & \cdots & u’‘ {(n,2)} \
\vdots & \vdots & \ddots & \vdots \
u’‘ {(1,m)} & u’‘ {(2,m)} & \cdots & u’‘_{(n,m)}
\end{bmatrix} \tag{9}
$$

其中u(i,j)表示来自ith路段的jth数据集，u′(i,j)和u′′(i,j)表示u(i,j)的两个随机分量，即u(i,j)= u′(i,j)+ u′′(i,j)。该流程图详细实现了RSU计算。

2) 云中的复杂数据处理

根据第V.B节中关于安全数据收集的描述，向量N′和N′′分别被发送到CPA和CPB，随后在计算方中进行进一步处理，以完成复杂的计算，从而获得交通拥堵率c和时空相关矩阵G。

对于道路路段的交通拥堵率数据集C，给出了详细的实现方法。首先，使用c= 1/v⊥的公式，在CPA和CPB之间的计算过程中实现不泄露参与方数值的计算。其次，CPA和CPB将分别生成向量S′ =[1/2, 1/2,…, 1/2]1×w和S′′ =[1/2, 1/2,…, 1/2]1×w参与后续计算。注意，S′或S′′的数量对应于已知道路路段的数量，即w。第三步，CPA和CPB交互式地执行(C′, C′′) ← Mdiv((V′⊥, S′):(V′′⊥, S′′))。最后，CPA得到结果C′，CPB得到结果C′′。

以下算法是交通拥堵率向量C′和C′′的实现细节。

为了获得相关性矩阵G，通过CPA和CPB之间的交互计算，基于路段间的欧式距离来计算时空特征。假设有两个GPS点a=(lata, lona)和b=(latb, lonb)，我们可以通过以下公式计算欧式距离L。

$$
L = R \cdot \arccos(L_1 + L_2) \tag{10}
$$

其中L1= cos(lata) · cos(latb) · cos(lona − lonb)，L2= sin(lata) · sin(latb)。根据安全数据收集，a和b分别被拆分为两部分，例如a′=(lat′a, lon′a)，a′′=(lat′′a, lon′′a)，b′=(lat′b, lon′b)以及b′′=(lat′′b, lon′′b)。然后a′和b′共同存在，a′′和b′′也被合并。为了在不泄露a和b任何私密信息的情况下计算欧式距离，我们设计了一种称为Dis的安全距离计算协议，即(l1: l2) ← Dis(a: b)。接下来，将阐述L的更多计算细节。

1. 执行(va1 : vb1) ← Sin(lat′a : lat′′a)，(va2 : vb2) ← Sin(lat′b : lat′′b)，(va3 : vb3) ← Ecos(a: b)，(va4 : vb4) ← Mul(va1 : vb2)，以及(va5 : vb5) ← Mul(vb1 : va2)。
2. CPA计算va6 = va1 · va2 + va3 + va4和x′=lon′a − lon′b，CPB计算vb6 = vb1 · vb2 + vb3 + vb4和y′= lon′′a − lon′′b。
3. 在计算(va7 : vb7) ← Cos(x′: y′)和(va8 : vb8) ← Emul((va3, va7):(vb3, vb7))后，CPA计算va9 = va6 + va8，CPB计算vb9 = vb6 + vb8。
4. 计算方A计算l1 = R· va，计算方B根据协议(va : vb) ← Arccos(va9 : vb9)计算l2 = R· vb。

其中R是地球半径。根据上述执行步骤，我们可以得到GPS点a和b之间的欧式距离L，例如L= l1+ l2。因此Dis协议可表示为(l1:l2) ← Dis(a: b)。

对于整个道路网络，PPCS从N′和N′′中选择所需元素，以进一步构建矩阵

$$
\Theta’ = [[lat’ {(\perp,1)}, lon’ {(\perp,1)}], …, [lat’ {(\perp,n)}, lon’ {(\perp,n)}]]
$$

和

$$
\Theta’’ = [[lat’‘ {(\perp,1)}, lon’‘ {(\perp,1)}], …, [lat’‘ {(\perp,n)}, lon’‘ {(\perp,n)}]]。
$$

然后，纬度并采用Mdis协议计算经度距离，即将Dis中的a和b替换为Θ′和Θ′′,，即(D′: D′′) ← Mdis(Θ′: Θ′′)。注意，D′和D′′是距离矩阵D的组成部分。由于整个道路网络中有n个道路路段，因此D的维度为n×n。关于计算D的更多细节如下所述。

为了提取关键特征，将高斯核函数$e^{-\frac{d^2}{2\sigma^2}}$引入到我们的机制中[43],其中d定义任意两个GPS点之间的欧式距离，σ是一个相关系数，用于确定GPS点之间的影响。该参数σ基于贝叶斯框架从d²训练数据[44]中获得。我们依赖于$e^{-\frac{d^2}{2\sigma^2}}$生成时空相关矩阵G，利用所有道路路段已知历史数据的欧式距离结果。因此，G的形式定义如下。

$$
G =
\begin{bmatrix}
e^{-\frac{d^2_{11}}{2\sigma^2}} & e^{-\frac{d^2_{12}}{2\sigma^2}} & \cdots & e^{-\frac{d^2_{1n}}{2\sigma^2}} \
e^{-\frac{d^2_{21}}{2\sigma^2}} & e^{-\frac{d^2_{22}}{2\sigma^2}} & \cdots & e^{-\frac{d^2_{2n}}{2\sigma^2}} \
\vdots & \vdots & \ddots & \vdots \
e^{-\frac{d^2_{n1}}{2\sigma^2}} & e^{-\frac{d^2_{n2}}{2\sigma^2}} & \cdots & e^{-\frac{d^2_{nn}}{2\sigma^2}}
\end{bmatrix} \tag{11}
$$

如前所述，CPA拥有一个矩阵D′，而CPB拥有另一个矩阵D′′，例如D= D′+ D′′。为了计算D′和D′′之间的安全乘法，我们给出以下步骤：

1. To execute(L′a : L′b) ← Mmul(D′: D′′);
2. CPA computes $W_1 = \frac{1}{2\sigma^2} \cdot (D’^2 + 2 \cdot L’_a)$;
3. CPB computes $W_2 = \frac{1}{2\sigma^2} \cdot (D’‘^2 + 2 \cdot L’_b)$;
4. Accomplishing(La : Lb) ← Rexp(W1: W2).

执行完上述协议后，我们可以得到由高斯核函数G生成的正交特征向量基。根据公式G= ΨΛΨ⁻¹，G被对角化为三个部分Ψ、Λ和Ψ⁻¹。此处，可将Ψ视为压缩感知稀疏表示矩阵，该矩阵被随机划分为Ψ1和Ψ2。然后，将Ψ1和Ψ2分别发送给CPA和CPB。接下来，Ψ1和Ψ2协助NSP基于若干已知值来估计未知的交通拥堵率。具体而言，Ψ的形式也通过

时空信息p如下。

$$
\Psi =
\begin{bmatrix}
p_{11} & p_{12} & \cdots & p_{1n} \
p_{21} & p_{22} & \cdots & p_{2n} \
\vdots & \vdots & \ddots & \vdots \
p_{n1} & p_{n2} & \cdots & p_{nn}
\end{bmatrix} \tag{12}
$$

为了更详细地展示云中的复杂计算，该过程可在图6中表示。

D. 安全的未知数据估计

如上所述过程，我们可以从n条道路的w个道路路段中获取T′(w << n)期间的交通拥堵率。即，CPA拥有一个向量C′=[c′1, c′2,…, c′w]，CPB存在一个向量C′′=[c′′1, c′′2,…, c′′w]。然后，TPS随机生成测量矩阵Φ ∈ Rw×n，NSP接收向量C′、C′′、Φ、Ψ1和Ψ2。最终，我们可以得到公式()，其中包含所有道路路段的交通拥堵率。最后，NSP可以通过优化算法获得C，并通过地图应用发布交通状况。

VI. 安全与性能分析

在本节中，我们将根据第四节B部分定义的安全模型，说明我们的系统模型在实现交通监控方面的安全性，并分析和论证所提出算法的效率。

A. 安全分析

定理VI.1 ：本文中的车辆数据传输过程是安全的。根据本文提出的数据传输策略，即使攻击者A1在传输过程中截获了数据，也无法推断出原始数据。

Proof : 在本文中，数据传输策略是将生成的数据随机分割成两部分，并通过两个不同的信道传输到两个不同的设备。假设数据项a被随机分割为a1和a2。由于分割的随机性，即使A1截获了a1或a2，也无法从a1和a2推断出真实值。

定理VI.2 : 本文中的安全计算协议在半诚实攻击者A2存在的情况下被安全执行，以实现密文上的明文计算的数据处理。

证明 ：当数据被发送到路侧单元时，所有计算步骤都在密文上执行以综合数据。即使攻击者以半诚实的方式攻击路侧单元并进一步获得综合数据，也无法从综合数据中推测出真实值。在本文中，计算方的数据处理是通过设计实现的安全计算协议，我们只需保证协议的安全性。这些安全计算协议在附录中给出。

定理VI.3 : 本文中的PPCS机制是安全的，能够保护车辆数据隐私并避免中间结果的泄露。半诚实攻击者A3即使获得了数据，也无法推断出原始数据。

证明 ：在PPCS中，车辆将随机分割生成的数据分为两部分，并发送给两个不同的RSU。由于分割具有随机性，即使A3截获了数据的一个分量，攻击者也无法猜测真实值。随后，RSU接收并整合数据分量，获得道路路段平均速度v(i,⊥)和时空特征lat(i,⊥)与lon(i,⊥)等中间结果。接着，v(i,⊥)、lat(i,⊥)和lon(i,⊥)也被分别随机分割为两部分，发送给CPA和CPB。通过云平台交互计算，得到交通拥堵率ci和时空相关矩阵G。由于信息融合，A3无法通过攻击ci和G推断出真实数据。最后，NSP通过两条不同的通信信道获取ci，并基于一些已知交通拥堵率估计所有路段的交通拥堵率，而无需推断真实值。

B. 性能分析

在本节中，我们从计算成本、通信开销和拥堵估计误差三个方面评估所提出的PPCS机制的性能。我们使用了源自中国福州市2015年5月的真实世界车辆数据，共计近两百万条。此外，模拟实验基于整个道路网络中的3000个路段进行。

1) 计算成本

对于所提出的PPCS机制，当车辆a生成记录R=[v, lat, lon, t]时，它在Q+中执行两个操作以生成随机数R1并计算R2= R − R1作为加密数据。在收集车辆数据后，路侧单元将接收到的数据进行整合，获得基于不同道路路段的计算方计算所需的中间值P。此外，路侧单元还将中间值分为两部分Pi和Pj，作为加密数据分别发送给CPA和CPB。随后，计算方基于Pi和Pj执行一系列复杂计算以实现交通监控。最后，通过获取少数道路路段的交通拥堵率，NSP利用CS恢复算法估算未知路段的交通状况的值。与运行时间相比，计算方和NSP执行复杂计算所需的时间更为显著。此处，我们用ce1、ce2、ce3和ce4分别表示车辆阶段、路侧单元阶段、云阶段和NSP阶段的计算成本。然后，PPCS的总计算开销将被计算为ce = ce1 + ce2 + ce3 + ce4。具体而言，我们提出的PPCS机制使每辆车可通过秘密共享向路侧单元发送其多个数据，并且来自同一道路路段的海量数据可被整合为一个值，从而节省大量计算成本。为了比较PPCS的效率，一种传统方法以Paillier表示，它在相应的道路路段对每个个体信息进行加密。我们列出了不同阶段的计算成本，并通过大量实验评估了所提出的PPCS机制在不同数据量下的性能。实验环境采用配备英特尔酷睿i7‐2445U处理器和16GB内存的计算机来模拟计算能力。所有实验均执行20次，以进一步选取平均结果。我们首先比较了实现PPCS的四个基本阶段，旨在展示数据保护的计算效率。从图7可以看出，随着数据量的增加，四个不同阶段的运行时间也随之增加，但每个阶段所需时间并未显著上升，而是呈现出线性增长的趋势。当加密数据量为3000时，运行时间仅为53秒，其中大部分时间消耗集中在NSP阶段。因此，我们设计了一种具有高效数据处理能力的PPCS机制。为了评估所设计协议的性能，我们将NSP阶段的最长耗时与基于一次性算法的Paillier进行比较（对于Paillier，变量N设置为2048，以生成两个1024位的大素数p和q）。同时，我们给出了NSP和Paillier在六种不同数据量下运行20次的平均时间消耗。从表I可知，PPCS的时间消耗最多比Paillier低500倍。为了说明PPCS的效率，我们还将其计算成本与KDSP[40]和CLASC[41]方法进行了比较。图7(c)中的结果表明，在不考虑驾驶员认证的情况下，PPCS在实现交通拥堵检测方面的运行时间优于其他方案。因此，我们可以得出结论：使用PPCS完成隐私保护交通监控能够大幅节省时间，降低交通监控的延迟时间。

2) 通信开销

我们分析了所提出的PPCS的通信开销，其中包括四个部分，即车辆到路侧单元通信、路侧单元到云平台通信、云平台A与云平台B交互、云平台到网络服务提供商通信，以及与KDSP和CLASC其他方法的比较。此处，我们以千字节为单位来衡量通信开销，千字节的测量基于IEEE 754标准。任何以单精度浮点数存储的值需要32位（1位用于符号位，8位用于指数部分，23位用于尾数部分），而双精度浮点数需要64位（1位用于符号位，11位用于指数部分，52位用于尾数部分）。对于车辆到路侧单元通信，每辆车辆生成其驾驶报告并将其传输至路侧单元。回顾我们之前的描述，车辆的报告在任意道路路段中被定义为数据集R=[v, lat, lon, t]，其中每个元素作为单精度浮点数需要32位。因此，R相当于4个单精度浮点数数据的比特数。然后，数据集R被随机划分为两部分R1和R2，其中R1和R2中的每个元素均为单精度浮点数数据。对于路侧单元到云平台通信，我们只需传输由路侧单元初步处理后的中间结果数据。假设有若干上报数据集位于道路路段a中，我们给出了生成的数据集R与传输数据之间的通信开销对比，如图8(a)所示。

对于CPA到CPB，由于CPA与CPB之间的数据处理需要交互式通信，我们根据所设计的协议，在不同基于云的情况下给出了交互轮数，如表II所示。实际上，在路侧单元完成初始数据处理后，同一路段内的大量上报数据被合并为单一数据项。随后，该数据项被随机分为两部分，分别发送给CPA和CPB。当然，由于Arccos、Emul、Mmul、Mdiv协议是基于乘法协议设计的，不同的协议具有不同的交互轮数和接收密钥次数。并且，已知计算方中各协议的轮数后，可得到如图8(b)所示的交互数据总比特数。

在图8(c)中，我们可以看到具有不同γ值的道路路段数量存在较大差异，γ值越高，数据传输量越小。更重要的是，我们在NSP中采用压缩感知（CS）技术，基于少量已知道路路段实现对未知道路路段的估计。为了实现实时交通监控，利用少量已知值快速估计其他未知数据更具意义。然而，由于在不同γ下的数据估计误差差异较大，因此我们需要通过不同的γ值来确保数据估计的准确性。此外，与KDSP和CLASC的对比结果如图8(d)所示。从图8(d)可以看出，PPCS在不考虑驾驶员认证的情况下优于其他方案。更重要的是，我们将一天划分为高峰时段和非高峰时段，并将一周划分为工作日和非工作日。如图9所示，我们可以得知在工作日期间每天有两个拥堵时段，且拥堵时段恰好与通勤时间一致。为了进一步说明未知数据估计的性能，我们将选择不同的时间段来估计城市整个道路网络的交通拥堵情况。

3) 交通拥堵估计

本文选择t=5 min[45]来评估所提出的PPCS的有效性。具体而言，我们通过NSP估计未知道路路段的交通拥堵率，并将其与传统的KNN算法进行比较。为了评估我们方案的性能，交通拥堵率的估计误差定义如下。

$$
e = \frac{|c_{re} - c|_2^2}{|c|_2^2} \tag{13}
$$

其中cre是估计的未知交通拥堵率，c是已知的交通拥堵率。

KNN算法估计误差。(b)PPCS与KNN算法的比较。)

图10(a)展示了不同K值下的拥堵估计误差。当K值为4时，KNN算法具有最佳的估计性能。我们利用PPCS通过基于不同γ值的高精度恢复算法实现实时交通监控。为了说明PPCS的性能，我们给出了关于拥堵时段和平稳时段的两条不同估计曲线，并选择在K=4时的KNN算法与PPCS进行比较。从图10(b)可以看出，随着γ值的减小，三种不同曲线的估计误差均降低。并且PPCS在拥堵时段和平稳时段的性能优于KNN算法。例如，使用PPCS仅需采集一半数量的道路路段数据即可达到良好的交通估计效果。因此，显然我们提出的PPCS具有更高的应用价值。

七、结论

本文中，我们采用隐私保护压缩感知机制，通过收集车辆数据实现实时交通监控。为了加快数据处理速度，我们将数据处理分为两部分，并设计了一系列合适的安全计算协议。更重要的是，我们利用压缩感知技术提升实时交通监控能力，并通过少数已知道路路段的交通拥堵率来推断整个道路路段的交通状况。从安全分析和性能评估的角度来看，我们的PPCS机制能够取得更好的效果。最后，我们在真实世界数据集上通过计算成本和通信开销验证了PPCS的有效性。