【Matlab】灰色关联分析

原创已于 2025-12-05 21:40:01 修改 · 1.8k 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #数学建模 #数据处理

于 2025-11-22 18:24:43 首次发布

1. 灰色系统

1.1 定义

“部分信息已知、部分信息未知” 的不确定系统

“全已知”（白色系统）， “全未知”（黑色系统）

1.2 3个核心特征

信息不完全性：系统的结构、参数、边界条件、输入输出关系中，至少有一项是未知或模糊的。例：分析 “用户转化率” 系统 —— 已知影响因素有 “浏览时长、点击次数”（部分信息），但未知 “用户隐性需求、竞品干扰” 等因素（部分信息未知），因此是灰色系统。
数据稀疏性：系统可观测的数据量少（小样本），无法通过传统统计方法（如回归分析）捕捉规律。例：电路仿真中，受限于实验成本，仅采集到 5 组 “电阻、电容与输出电压” 的对应数据（小样本），无法用正态分布假设建模，属于灰色系统。
不确定性与非线性：系统内部因素之间、因素与目标之间的关系是非线性、非确定性的，无法用简单的线性方程描述。例：“传感器测量精度” 系统 —— 温度、湿度对精度的影响不是 “温度每升高 1℃，精度下降固定值”，而是复杂的非线性关系，且存在环境噪声干扰（不确定性），属于灰色系统。

2. 为什么需要灰色关联分析

传统分析方法的局限：

数据要求高：传统方法需要大量数据（样本量≥30）、数据服从正态分布，且要求信息完全明确；
抗干扰能力弱：对异常值敏感，小样本、非平稳数据（如电路瞬态测试数据、短期用户行为数据）下结果不可靠；
量纲依赖强：不同因素单位不同（如电压 V、温度℃、用户浏览时长 s），直接计算会导致结果偏差；
非线性适配差：现实中因素与目标的关系多为非线性，传统线性分析难以捕捉。

灰色关联分析正是为解决这些痛点而生 —— 它不依赖数据分布、不要求大样本，能处理模糊、不完全、非线性的系统，用简单的量化方法打通 “未知信息” 与 “已知数据” 的关联

3. 研究什么问题（会得到什么结论）

核心是解决 “多因素对单一目标的影响程度排序问题”，具体可拆解为 3 类典型问题：

“影响因素识别” 问题：目标变量（如电路输出电压、用户转化率）受多个因素（如电阻、电容；浏览时长、点击次数）影响，需明确 “哪些因素是关键影响者”；
“因素重要性排序” 问题：多个影响因素中，需量化 “谁的影响更显著”（如 “温度对传感器精度的影响是否比湿度大”）；
“系统趋势一致性” 问题：判断各影响因素与目标变量的变化趋势是否同步（如 “电压升高时，输出功率是否同步升高”，趋势越同步，关联度越高）。

以上是灰色关联分析的引子，下面是灰色关联分析的思想，具体的实现，以及实现细节

4. 核心思想

“趋势同步性即关联度”

“两个序列的变化趋势越同步、差异越小，它们的关联度越高；反之则越低”

5. 代码之前的理论解释和知识储备

5.1 数据

在你面前有一些数列

参考数列（母数列）：反映系统行为特征的数据序列，记作 $x_{0}$

比较数列（子数列）：影响系统行为因素组成的数据序列，记作 $x_{i}(i = 1,2 ... n)$

可以这样理解：参考序列看作因变量 $y$ ，比较序列看作自变量 $x$

在网上找了个例子（如图）—— 数据纯属虚构......仅用于数学分析

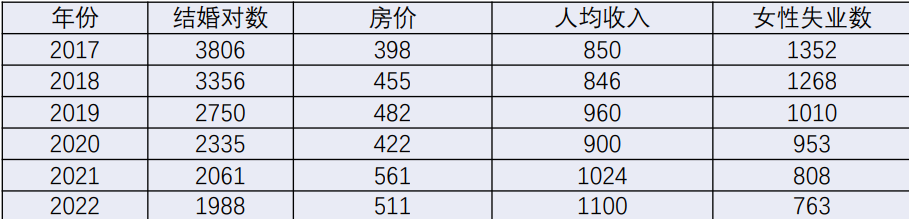
结婚对数是参考数列 $(y)$ ；房价，人均收入，女性失业数是比较数列 $(x)$

我们需要研究：

哪些因素是主要因素，哪些是次要因素；哪些对系统发展影响大，哪些影响小。从而进行系统分析，强化推动因素，抑制阻碍因素

整个灰色关联分析可以分成两个大的步骤：

一个是数据预处理，一个是确定灰色关联系数

5.2 数据预处理

子母数列各有特点：随年份增加，有的上升有的下降；有的指标越大越好（人均收入），有的指标越小越好（放假，女性失业数），有的指标落在某个区间最好（比如买房子，离市中心太近太吵，离市中心太远出行又不方便，在理想范围内都是满分，超过范围开始扣分），有的指标越靠近某个值越好（比如人的体温，越靠近 $36.5^{\circ}$ 越好）

所以我们对数据分类：分为极大型（越大越好），极小型（越小越好），中间型（越靠近理想值越好），区间型（区间内最好）；其中极大型指标标也被称为——效益型指标，极小型指标也被称为——成本型指标

为了统一评价标准，我们需要将所有指标全部转为极大型，namely实现数据的正向化

5.2.1 正向化处理

极小型转极大型： $max - x$

中间型转极大型：

最大差距值： $M = \left \{ |x_{i} - x_{best} \right \}$ $\tilde{x}_{i} = 1 - \frac{|x_{i} - x_{best}|}{M}$

区间型转极大型：

最大差距值： $M = max\left \{ a - min\left \{ x_{i} \right \},max\left \{ x_{i} \right \} - b \right \}$ $a,b$ 为区间左右边界

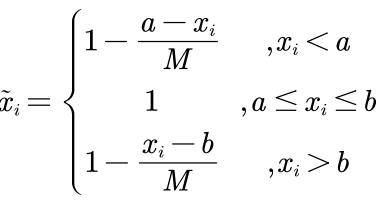
5.2.2 标准化处理

将不同量纲、不同数值范围的指标，映射到统一的数值区间（如 [0,1] 或 [-1,1]），消除数值尺度和量纲的影响

以下列举几个常见的标准化处理方法：

1. min-max 标准化（归一化，映射到 [0,1]）

${x}' = \frac{x_{i} - x_{min}}{x_{max} - x_{min}}$ （原始数据，指标最大最小值，标准化后的数据）

2. z-score 标准化（标准化为均值 0、方差 1）

${x}' = \frac{x_{i} - \bar{x}}{s}$ （ $\bar{x} = \frac{1}{n}\sum x_{i}$ ， $s = \sqrt{\frac{1}{n-1}\sum (x_{i} - \bar{x})^{2}}$ ， ${x}'$ 标准化后的数据）

解释：为什么这里是 $\frac{1}{n - 1}$

明确：

大多数情况我们的统计都是抽样调查，所以 $\bar{x}$ 表示的是样本均值

样本均值 $\bar{x}$ 的性质：“最小偏差平方和性质”——对任意一个样本，样本均值 x̄是使得 “样本内所有数据与它的偏差平方和最小” 的唯一值 ，我们聚焦于“偏差平方和”，用样本均值计算“偏差平方和”一定是最小的

计算 “能反映总体真实情况的方差” 时，我们理想中想用 “总体均值 μ”，但实际只能用 “样本均值 $\bar{x}$ ”，而 $\bar{x}$ 与总体均值或多或少存在些许细微偏差，导致低估总体方差，所以需要用 n-1 修正

数学上的修正逻辑：通过大量统计证明，当分母用 $n-1$ 时，样本方差是总体方差 $s^{2} = \frac{1}{n-1}\sum (x_{i} - \bar{x})^{2}$ 是总体方差 $\sigma ^{2}$ 的 无偏估计（即样本方差的期望等于总体方差）

3. 初值化标准化

${x}' = \frac{x_{i}}{x_{1}}$

$x_{1}$ 该指标的第一个数据点（初值）

${x'}$ 标准化后的数据（起点为 1，后续数据为相对初值的倍数）

以每个指标的 “第一个数据点为基准”，所有数据除以该基准值，使序列起点统一为 1，突出数据的 “相对变化趋势”

4. 均值标准化

${x}' = \frac{x_{i}}{\bar{x}}$

我们采用第四种“均值标准化”，处理完毕后的数据

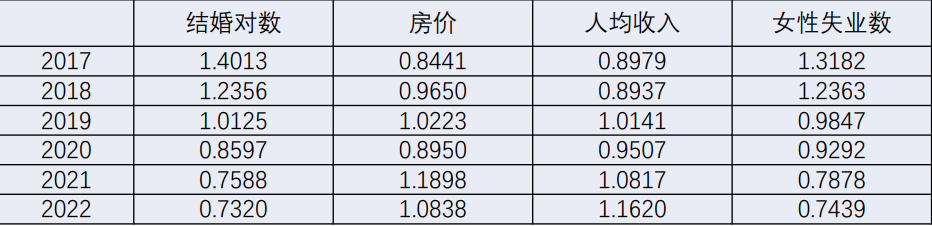
5.3 灰色关联系数

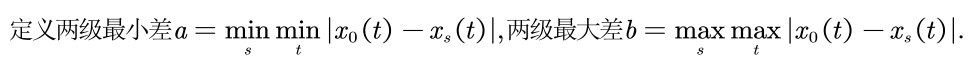
这里的两个 $min min ,maxmax$ 表示在两个维度同时取最值（其实相减之后，所有数据中的最小值最大值）

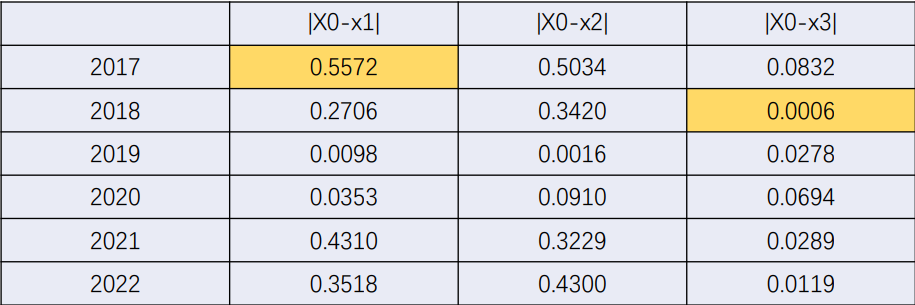
对上表中每一个元素定义为：

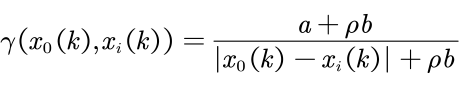
得到灰色关联系数，其中 $\rho$ 为分辨系数，一般取0.5

纵列取和得到灰色关联度

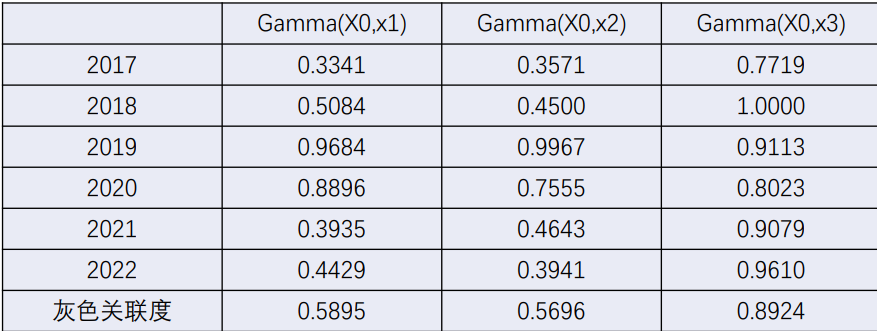
灰色关联度越大，相应序列关联度就越大，对系统的影响越大

解释灰色关联度公式

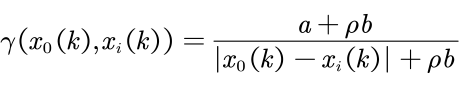
分子：“最小差 + 分辨系数 * 最大差”

分母：“当前绝对差 + 分辨系数 * 最大差”

分子上面的最小差对分子值的影响不大，更大的意义是将关联系数的值域定在（0, 1]而不是（0, 1）

6. Conclusion

数学建模其实是一件很有意思的事情，Matlab也是一个很强大的工具。这里面“灰色关联系数”的公式重要吗，其实没多重要，问AI很快就能知道。我觉得更重要的是，正向化，标准化，以及没有涉及的归一化，还有 z - score 标准化中方差计算为什么用 $\frac{1}{n-1}$ .这些是对数据的处理方法，在概统里面，这些处理方法非常常见，大抵可以比喻成数学的树干，“灰色关联分析”更像是树的枝叶。

学数学建模的过程中，“灰色关联分析”算是印象比较深刻的存在，其实也就是因为我知道了什么是正向化，归一化，标准化，觉得特别有意思。

（最后将小厮的代码附上）

7. 代码

x = xlsread('灰色关联分析date.xlsx');
X = x';    %对矩阵进行元素的转置


%%
%使用正向化和标准化的前提，必须第一行是指标，第一列是对象
disp('正向化');
vec = input('以数组形式输入待正向化的向量组，[1,2,3]表示1,2,3列需要正向化，不需要则输入-1\n');
if (vec ~= -1)                  %  ~= 表示“不等于”
    for i = 1 : size(vec,2)
        flag = input(['第' num2str(i) '列是哪类数据（1.极小型 2.中间型 3.区间型）']);
        if (flag == 1)
            X(:,vec(i)) = min2max(X(:,vec(i)));
        elseif (flag == 2)
            best = input('请输入最适中间值：\n');
            X(:,vec(i)) = mid2max(X(:,vec(i)), best);
        else
            interval = input('请输入最适区间（以"[a,b]"形式输入：\n');
            X(:,vec(i)) = int2max(X(:,vec(i)),interval(1),interval(2));
        end
    end
end
disp('正向化完成')


%%
disp('标准化');
[m,n] = size(X);
square_x = (X .* X);
sum_x = sum(square_x) .^ 0.5;
stand_x = X ./ repmat(sum_x,m,1);
disp(stand_x);
disp('标准化完成');


%%
disp('进行灰色关联分析');



%Method1
%gra = [res,max(res,[],1)];添加一个列向量在矩阵的右边
%添加一个行向量在矩阵的底部
gra = [stand_x; max(stand_x, [], 1)];
[r,c] = size(gra);
gamma = zeros(r,c);    %zero是方阵，zeros是矩阵
                       %对于已知规模的大型矩阵，最好提前用zeros/ones声明尺寸，再通过索引赋值
                       %为了在后面和gra矩阵维度匹配，这里不可以zeros(r-1,c)
                       %gamma gra 7*9矩阵
disp('求灰色关联系数');
%一行一行拼接得到gamma
for i = 1 : r
    gamma(i,:) = abs(gra(i,:) - gra(r,:));
end
Gamma = gamma((1:r-1),:);



%Method2
%一列一列拼接得到gamma
%for i = 1 : c
%   gamma = (:,i) = abs(gra(:,i) - gra(r,i));
%end
%Gamma = gamma((1:r-1),:);
disp('Gamma');

Min = min(Gamma);
Max = max(Gamma);
Discrimination = 0.5;
Coefficient = (Min + Discrimination * Max)./(Gamma + Discrimination * Max);

disp('求灰色关联度');
Grade = sum(Coefficient,2)/c;
disp(Grade);



%%
function [ret] = min2max(a)%形参，接受实参，不同函数形参可以使用相同的名称，形参具有局部作用域
    ret = max(a) - a;
end
function [ret] = mid2max(a,mid)%形参的定义在函数声明时完成，不需要提前定义
   ret = 1 - abs(a - mid) / max(abs(a - mid));
end
function [ret] = int2max(s,a,b)%函数被调用时，Matlab自动根据传入的实参为形参分配内存和赋值
    M = max(max(s) - b,a - min(s));
for i = 1 : size(s)%因为自动根据实参调整，所以这里直接size(s)
    if s(i) > b
        s(i) = 1 - (s(i) - b) / M;
    elseif s(i) < a
        s(i) = 1 - (a - s(i)) / M;
    else
        s(i) = 1;
    end
end
ret = s;
end