Mujoco-欠驱动的二阶单摆的LQR控制

Feisy

已于 2022-02-20 21:55:28 修改

阅读量743

点赞数 1

CC 4.0 BY-SA版权

分类专栏： Mujoco 文章标签： mujoco

于 2022-02-20 20:43:00 首次发布

本文链接：https://blog.youkuaiyun.com/feisy/article/details/123035630

这段代码展示了使用MuJoCo库进行动力学模拟和控制器设计的过程。函数`f`实现了从状态到输出的动力学方程，通过计算雅可比矩阵A和输入矩阵B来求解LQR控制器。同时，给出了一个双连杆摆动的MuJoCo模型，包括世界背景、两个连杆、关节和传感器定义。在主函数中，实现了控制器初始化、数据保存和模拟循环，用于实时控制和数据记录。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

MuJoCo Lec7

在这里插入图片描述

void f(const mjModel* m, mjData* d,double input[5], double output[4])
{
   
   
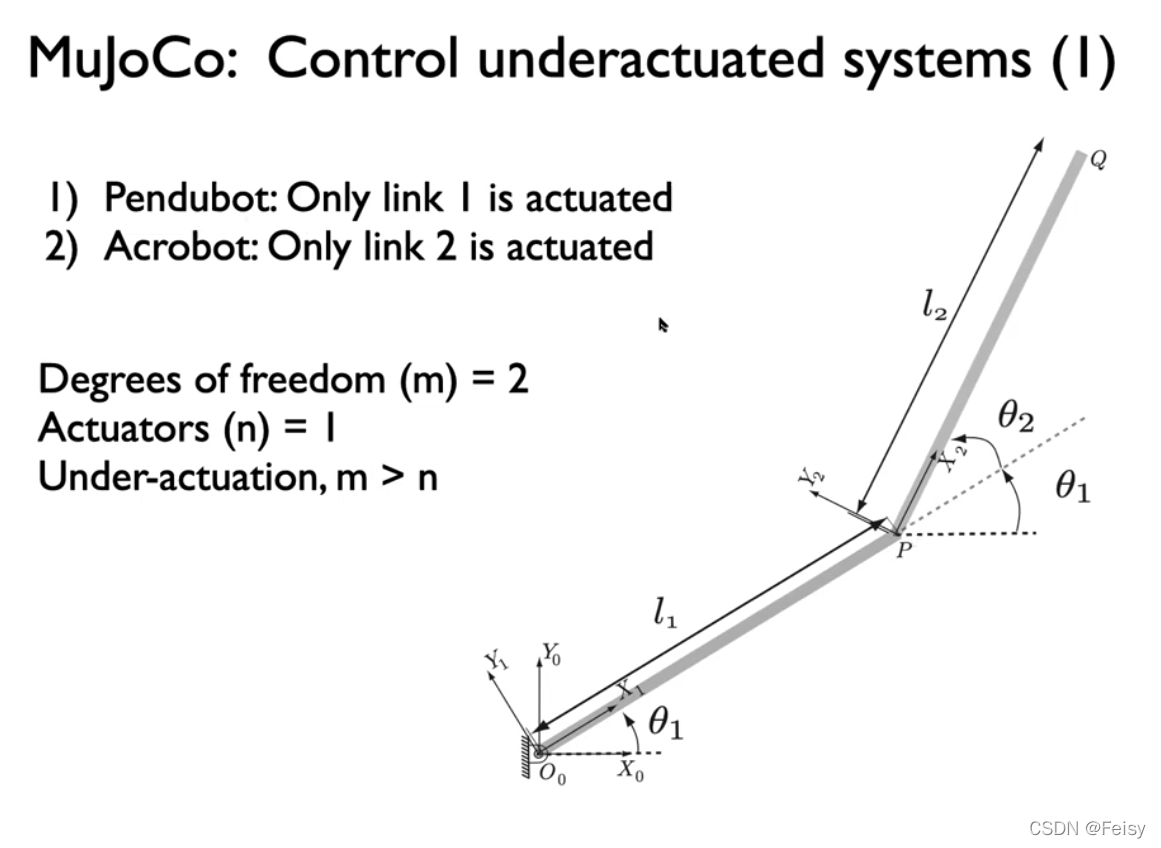
  //state = q1, q1dot, q2, q2dot
  //inputs = q1, q1dot, q2, q2dot, u
  //outputs = q1dot, q1ddot, q2dot, q2ddot

  d->qpos[0] = input[0];
  d->qvel[0] = input[1];
  d->qpos[1] = input[2];
  d->qvel[1] = input[3];
  d->ctrl[0] = input[4];
  //Forward dynamics: same as mj_step but do not integrate in time.
  mj_forward(m,d);

  double q1dot, q2dot;
  q1dot = d->qvel[0];
  q2dot = d->qvel[1];

  //Equation of motion
  //M*qacc + qfrc_bias = ctrl
  //qacc = inv(M)*(ctrl-qfrc_bias) = q1ddot, q2ddot
  int i;
  const int nv = 2;
  double M[nv*nv] = {
   
   0};
  mj_fullM(m,M,d->qM);
  //M = {M[0] M[1]; M[2] M[3]}
  double det_M = M[0]*M[3] - M[1]*M[2];
  double Minv[] = {
   
   M[3],-M[1],-M[2],M[0]};
  for (i=0;i<4;i++)
    Minv[i] = Minv[i]/det_M;

  //printf("%f %f %f %f \n",M[0],M[1],M[2],M[3]);

  double qacc[nv]={
   
   0};
  double f[nv]={
   
   0};
  //f = (ctrl-qfrc_bias)
  f[0] = 0-d->qfrc_bias[0]; //no ctrl because there is no control on link 1
  f[1] = d->ctrl[0]-d->qfrc_bias[1];
  //printf("%f %f \n",f[0],f[1]);

  //qacc = inv(M)*(ctrl-qfrc_bias)
  mju_mulMatVec(qacc,Minv,f,2,2);

  double q1ddot = qacc[0];
  double q2ddot = qacc[1];

  output[0] = q1dot;
  output[1] = q1ddot;
  output[2] = q2dot;
  output[3] = q2ddot;

}

在这里插入图片描述

A矩阵，通过给q一个微小的干扰，然后运动5的公式得到

A有四列，所以这里重复了四次

int i,j;
 double input[5]={
   
   0};
 double output[4]={
   
   0};
 double pert = 0.001;

 //input[0] = 0.1;
 //input[1] = 0.1;
 //input[4] = 0.1;
 double f0[4] = {
   
   0};
 f(m,d,input,output);
 //printf("%f %f %f %f \n",output[0],output[1],output[2],output[3]);
 for (i=0;i<4;i++)
   f0[i] = output[i];

 double A[4][4]={
   
   0};

 j = 0;
 for (i=0;i<5;i++)
   input[i]=0;
 input[j] = pert;
 f(m,d,input,output);

//因为是q1发生变化，所以，我们求的是f对q1的导数，这种思想其实
//是微分的数值化计算
 for (i=0;i<4;i++)
   A[i][j] = (output[i]-f0[i])/pert;

j = 1;
 for (i=0;i<5;i++)
   input[i]=0;
 input[j] = pert;
 f(m,d,input,output);
 for (i=0;i<4;i++)
   A[i][j] = (output[i]-f0[i])/pert;

 j = 2;
 for (i=0;i<5;i++)
   input[i]=0;
 input[j] = pert;
 f(m,d,input,output);
 for (i=0;i<4;i++)
   A[i][j] = (output[i]-f0[i])/pert;

 j = 3;
 for (i=0;i<5;i++)
   input[i]=0;
 input[j] = pert;
 f(m,d,input,output);
 for (i=0;i<4;i++)
   A[i][j] = (output[i]-f0