非线性最小二乘

最新推荐文章于 2022-04-09 12:17:37 发布
原创 最新推荐文章于 2022-04-09 12:17:37 发布 · 735 阅读 · 1 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

非线性最小二乘

非线性最小二乘问题是求解目标参数Ｘ的最优值的方法．

关键要素：

1.　要有待优化的参数X
2.　要知道参数与估计值的函数关系．f(X)
3.　要有观测数据Z
4.　待优化参数的初值X0
5. 待优化参数的范围(可选)

一般形式：

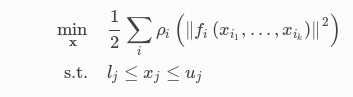
在这里插入图片描述

非线性优化与非线性最小二乘

非线性最小二乘问题，可以转化为非线性优化问题．解非线性最小二乘需要非线性优化算法．非线性优化算法最通用的方法是梯度下降．

非线性最小二乘的要求解的参数，作为非线性优化的Ｘ因此判断一个最小二乘问题是线性还是非线性的依据是参数与观测之间是线性还是非线性．
例如求解y=ax2其实就是线性最小二乘问题，而y=a2x是非线性最小二乘问题．

非线性最小二乘求解方法详解
陈建驱的博客
02-21 1万+
个人博客：http://www.chenjianqu.com/ 原文链接：http://www.chenjianqu.com/show-85.html 最小二乘法 最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。数...
非线性最小二乘法
weixin_42470012的博客
01-03 3655
最近和学长论文里面的LM算法较上劲了，明明只是构建了简单的雅可比矩阵用CV::solve求解的，通篇鼓吹自己的LM算法，我奇怪了，怎么还有两步LM优化，还说是以上一步中的结果作为下一步优化的约束，明明不存在约束的关系啊，只是把它分成了两步来做。 我实在是难以复现他的过程，我准备自己写一个LM算法。论文里面这一部分是用来优化transformCur这个矩阵数组的， 我们先来把它这个数学模型复现一下，...
最小二乘法非线性方程
10-30
把非线性的点，通过最小二乘法进行线性拟合，把非线性的点做成线性方程。
非线性最小二乘法原理
热门推荐
daocaoren_的博客
03-29 1万+
一些基础概念[1] 1.最小二乘法定义 找到一个x∗{x^*}x∗，使得下面的式子到达局部最小值， F(x)=12∑i=1m(fi(x))2F(x) = \frac{1}{2}\sum\limits_{i = 1}^m {{{({f_i}(x))}^2}}F(x)=21​i=1∑m​(fi​(x))2这里的fi(x){{f_i}(x)}fi​(x)表示变量为xxx的函数，其中自变量xxx维度为nn...
基于非线性最小二乘算法的点云坐标转换研究
11-24
非线性最小二乘算法是一种在数据处理领域广泛使用的数学方法，尤其在需要精确处理点云数据时表现突出。点云是由大量点构成的集合，这些点通常来源于3D扫描仪或激光扫描设备的输出。每一点都拥有三个维度的坐标信息，...
精选资源
非线性最小二乘问题与Levenberg–Marquardt算法详解
01-07
目前来说，Levenberg–Marquardt 法可以说是求解非线性最小二乘问题的标准算法了，也就是应用十分广泛，例如运动参数估计、相机内部参数标定等等，其性能也是得到很多论文背书的。不过，一上来就扔出这么长的一串...
精选资源
非线性最小二乘问题.rar_非线性最小二乘算法
07-13
非线性最小二乘问题（Nonlinear Least Squares, NLS）是数据分析和科学计算中的一个常见问题，尤其是在无线通信领域。它涉及到寻找一组参数，使得由这些参数构成的非线性函数与观测数据之间的残差平方和最小。在无线...
非线性最小二乘问题,非线性最小二乘问题 LM,matlab
09-10
最优化方法中的非线性最小二乘法
精选资源
matlab精度检验代码-InvGN:计算Tikhonov正则化的高斯牛顿非线性迭代反演以解决阻尼非线性最小二乘问题（Matlab代码）
05-22
INVGN计算Tikhonov正则化的Gauss-Newton非线性迭代反演，以解决以下阻尼非线性最小二乘问题： minimize ||g(m)-d||^2_2 + lambda^2||Lm||^2_2 For appropriate choices of regularization parameter lambda, this ...
非线性最小二乘法C语言代码
10-10
非线性最小二乘法C语言代码 main () { int n,i,flag2; char flag1='y'; float ar[50],br[50],x,y,xe,ye,xye,xxe,sx,sy,sxy,sxx,a,b; printf ("\n欢迎使用最小二乘法数据处理程序\n");
优化方法的非线性最小二乘问题Matlab代码
11-03
优化方法的非线性最小二乘问题Matlab代码，有需要的可以来下载哦！
非线性最小二乘法辨识程序
07-06
非线性最小二乘法程序，用于参数辨识和分析。
非线性最小二乘法Matlab实现
12-28
非线性最小二乘法Matlab实现 f=x(1)*K^x(2)*L^x(3)-b; Cobb-Douglas生产函数
非线性最小二乘通俗易懂解释
kaggle expert，全球排名前1000，清华计算机研究生，兴趣算法工程
05-01 5270
1. 非线性最小二乘介绍 1.1.最小二乘问题回顾： 在上一篇博客中我们知道最小二乘问题是为了找到测量值和模型预测值之间的最小误差，该问题可以简单的表示为： 其中e(x)为模型和样本之间的误差，在SLAM中亦可以看作为观测值和估计值之间的误差。通过求解该问题我们就能够优化我们的模型函数使之更接近与真实的函数模型。 下图的数据拟合可以很好的说明...
[数值计算] 数据拟合——非线性最小二乘法
chengde6896383的专栏
12-25 541
https://zhuanlan.zhihu.com/p/83320557
非线性最小二乘， BA(Bundle Adjustment)
chaoqinyou的博客
04-09 4555
在看高翔博士的《视觉slam十四讲》，把看到的BA相关的东西记录一下，方便自己之后复习，有理解不对的地方，还请指正！ 一、非线性最小二乘 1.1 总体思路， 一阶法和二阶法 最小二乘问题 ，我们称F(x)是代价函数， f(x)是误差函数； 直接求再比较各个极值点/鞍点的大小一般是比较难的。因此， 一般采取迭代的方法： 即从某个初值x0开始，每一次寻找一个可以使得F(x)变小的增量delta_x， 当增量delta_x比较小的时候，我们就认为认为达到了极值。 一阶法寻找delta_x： 将F(x).
线性最小二乘和非线性最小二乘
最新发布
08-15
### 线性最小二乘与非线性最小二乘的区别 线性最小二乘（Linear Least Squares, LLS）和非线性最小二乘（Nonlinear Least Squares, NLS）是两种用于参数估计和模型拟合的重要方法，它们在数学原理、计算复杂度以及应用场景上有显著区别。 #### 1. 原理上的区别 - **线性最小二乘** 线性最小二乘法适用于模型可以表示为参数的线性组合的情况，其目标函数通常写作： $$ J(\theta) = \sum_{i=1}^{n}(y_i - f(x_i, \theta))^2 $$ 其中 $ f(x_i, \theta) $ 是线性函数，可以表示为 $ f(x_i, \theta) = \theta_1 \phi_1(x_i) + \theta_2 \phi_2(x_i) + \dots + \theta_p \phi_p(x_i) $，其中 $ \phi_j(x_i) $ 是已知的基函数。由于模型是参数的线性函数，因此可以通过解析方法（如正规方程）直接求解最优参数 $ \theta $。 - **非线性最小二乘** 非线性最小二乘适用于模型 $ f(x_i, \theta) $ 是参数 $ \theta $ 的非线性函数的情况。目标函数形式与线性最小二乘相同： $$ J(\theta) = \sum_{i=1}^{n}(y_i - f(x_i, \theta))^2 $$ 但由于 $ f(x_i, \theta) $ 是非线性的，无法通过简单的解析方法求解。通常需要使用迭代优化算法（如高斯-牛顿法、Levenberg-Marquardt算法）逐步逼近最优解。 #### 2. 计算复杂度与稳定性 - **线性最小二乘** 线性最小二乘问题可以通过正规方程求解，即 $ \theta = (X^T X)^{-1} X^T y $，其中 $ X $ 是设计矩阵，$ y $ 是观测值向量。这种方法计算效率高，且在数据量不大时非常稳定。 - **非线性最小二乘** 非线性最小二乘问题的求解依赖于迭代算法，通常需要提供初始猜测值，并通过不断调整参数来最小化目标函数。由于非线性优化问题可能存在多个局部极小值，因此对初始值的选择敏感，计算复杂度也较高。 #### 3. 应用场景 - **线性最小二乘的应用场景** 线性最小二乘适用于模型参数与输出之间呈线性关系的问题。例如： - 回归分析中的线性拟合问题 - 工程测量数据的线性校正 - 经济学中的线性回归模型 - **非线性最小二乘的应用场景** 非线性最小二乘适用于模型输出与参数之间呈非线性关系的问题。例如： - 化学反应动力学建模 - 生物医学数据的非线性拟合 - 信号处理中的非线性系统辨识 - 机器学习中的非线性回归模型 ### 示例代码：线性与非线性最小二乘拟合 #### 线性最小二乘拟合示例（Python） ```python import numpy as np from numpy.linalg import inv # 生成线性数据 x = np.linspace(0, 10, 100) y = 2 * x + 1 + np.random.normal(0, 1, 100) # 构造设计矩阵 X = np.vstack([x, np.ones(len(x))]).T # 求解线性最小二乘问题 theta = inv(X.T @ X) @ X.T @ y print(f"拟合参数: 斜率 = {theta[0]:.2f}, 截距 = {theta[1]:.2f}") ``` #### 非线性最小二乘拟合示例（Python） ```python from scipy.optimize import curve_fit # 定义非线性模型 def nonlinear_model(x, a, b): return a * np.exp(b * x) # 生成非线性数据 x = np.linspace(0, 5, 50) y = 2 * np.exp(0.3 * x) + np.random.normal(0, 0.5, 50) # 拟合非线性模型 popt, _ = curve_fit(nonlinear_model, x, y) print(f"拟合参数: a = {popt[0]:.2f}, b = {popt[1]:.2f}") ``` ### 总结 - **线性最小二乘**适用于模型参数与输出呈线性关系的问题，计算简单且稳定，适合大规模数据处理。 - **非线性最小二乘**适用于模型输出与参数之间呈非线性关系的问题，计算复杂度较高，但能处理更广泛的模型形式。 ---
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值