一种基于电路模型引导的短路自激电磁带隙谐振天线设计 流程与效率估算
梅赫迪·侯赛尼
爱德华·S·罗杰斯电气与计算机工程系,国王学院路10号,多伦多,安大略省,加拿大 M5S 3G4
通讯应联系梅赫迪·侯赛尼;mehdi.hosseini@utoronto.ca
2016年2月25日收到;2016年5月1日修订;2016年5月10日接受
学术编辑:朴翼模
版权所有 © 2016 梅赫迪·侯赛尼。本文是一篇开放获取文章,遵循知识共享署名许可协议发布,允许在任何媒介中不受限制地使用、传播和复制,前提是正确引用原始作品。
本文提出了一种用于计算高效设计平面短路自激式电磁带隙谐振天线(SC SE‐EBG‐RA)的电路模型。为此,将先前提出的适用于开路版本天线的同一电路模型进行修改,使其适用于短路版本。详细的HFSS建模与仿真验证了该模型在预测天线谐振方面的准确性。通过模拟惠勒罩法(WCM)计算所设计天线的效率,并与数值分析仪提供的标准效率进行比较。电磁建模过程中充分考虑了SMA连接器、不连续性以及惠勒罩(WC)的影响,以模拟实际惠勒罩测量,从而提高了结果的可信度。最终实现了一款尺寸为0.34λ × 0.30λ × 0.03λ的小型天线,其验证效率达到93%,且符合低成本制造工艺的要求。
引言
尽管电小天线(ESAs)已研究多年[1],但现代通信系统的近期繁荣才真正凸显了其重要性。从这一发展的积极方面来看,逐步向更高频率的转变带来了使用更短波长的机会,从而可以采用物理尺寸更小的天线。然而,用户对数据需求的不断增长持续给ESAs的设计带来了日益增加的压力。频段的激增以及在当前设计场景中尽可能容纳更多分配频段的愿望也加剧了这一局面。实现理想ESAs的主要挑战在于带宽(BW)、增益和天线电尺寸之间的基本[1, 2]折衷。在尝试减小天线电尺寸时,通常需要付出降低带宽或恶化辐射效率的代价,甚至两者兼有,这一事实使得天线小型化成为一种折衷的艺术[3]。与ESAs相关的主要研究方向之一是为这类电磁结构的设计开发计算高效的分析方法,以主要涉及开发准静态电路模型。电路模型可为设计人员提供一组初始值,用于耗时的设计优化过程,从而简化实现最优化电小天线的过程,即使在严格要求下也是如此。这类模型还能快速洞察性能与结构参数之间的关系[4],激发天线设计中更多的创新和更优的问题解决思路。如果天线具有周期结构[5–8],首先单独对单元胞进行建模[9, 10],然后将获得的知识应用于布洛赫[7, 11, 12]等理论,以理解由这些单元胞组成的整个周期性天线的性能。
最近提出的周期性ESAs示例之一是所谓的自激式电磁带隙谐振天线(SE‐EBG‐RA)[4, 8, 13, 14],该结构提出了基于布洛赫的电路模型。SE‐EBG‐RA最初在[7]中被引入,作为一种新型高效率平面ESA,其工作原理通过布洛赫图进行了解释。大多数典型的电磁带隙天线基于放置在高阻抗平面上的偶极子[15, 16]、贴片[17]或其他变体[18]构成,该高阻抗平面由多种单元组成。然而,将自激式电磁带隙谐振天线(SE‐EBG‐RA)与大多数传统电磁带隙天线区分开来的特点是其特殊的集成结构和辐射机制。少数级联的电磁带隙单元被视为一段高辐射传输线,该传输线在一侧通过微带线(MSL)直接激励(自激),而另一侧可以是开路[4, 7]、短路[13]、或甚至终端匹配[8]。这样,辐射体和电磁带隙单元构成一个统一的辐射结构。尽管在机理和结构上存在这些差异,但这类周期性天线的性能与其他电磁带隙天线非常相似。在此基础上,[4]提出了一种相对精确的基于布洛赫的电路模型,用于自激式电磁带隙谐振天线(SE‐EBG‐RA)的快速分析与设计,但该模型仅适用于单元一侧开路(开路型)的情况,形成开路型自激式电磁带隙谐振天线(OC SE‐EBG‐RA)。此外,这些方程仅对三个单元胞有效,尽管如后文[13]所示,这并非必要条件。
为补充[4],本文提出了一种新的广义模型,该模型不仅适用于OC SE‐EBG‐RA,也适用于任意单元数量的SC版本(第2节)。在第3节中,通过由所提出的电路模型引导的高效设计流程,设计了一个SC SE‐EBG‐RA示例。接着,在第4节中,对惠勒罩(WC)与所设计的天线进行建模,以数值估算天线的效率。详细的数值建模与分析提供了 η的两个独立估计值。随后,在第5节中给出了电磁模型的一种替代实现方式,最后在第6节中总结全文,并研究了天线接地板极端截断对其性能的影响。所有数值分析均使用高频结构仿真器(HFSS)完成。
2. SC SE‐EBG‐RA的电路模型
自激式电磁带隙谐振天线(SE‐EBG‐RA)由小型周期性金属贴片组成,这些贴片布置在接地的基板上,彼此之间具有微小间隙。该周期结构被视为一种周期性传输线,其色散关系为[4]
$$
\beta^2 = k^2 - \sqrt{\varepsilon_{\text{reff}}} Z_0 d C_g c,
$$
其中,k是无负载微带线(移除间隙后)的波数[4],c 为 $(\varepsilon_0 \mu_0)^{-1/2}$,d是单元尺寸,且必须远小于自由空间波长,以保证(1)的有效性。$Z_0$ 和 $\varepsilon_{\text{reff}}$ 也可由[4]中的方程求得。色散图的截止频率($f_c$) 表示为[4]
$$
\omega_c^2 = \frac{c}{Z_0 d C_g \sqrt{\varepsilon_{\text{reff}}}},
$$
其中 $C_g$ 是由相邻贴片之间的共面耦合($C_{cp}$)引起的电容。本文中忽略了[4]所考虑的平行板耦合,因为走线较细。如果 d 远大于间隙尺寸,如图 1 所示,则 $C_g = C_{cp} = 2C_{cp1} + C_{cp2}$,具体公式见图1(c)。
开放式SE‐EBG‐RA的 m单元谐振频率($f_r$)可以表示为
$$
\omega_r^2 = \omega_c^2 + \omega_p^2,
$$
其中 $\omega_r$ 是 $2\pi f_r$,且 $\omega_p$ 是
$$
\omega_p = \frac{c\pi}{nl\sqrt{\varepsilon_{\text{reff}}}},
$$
其中,对于[4]中的开路情况,n=2。同时,l=md,其中 m为单元数量。在[13]中已证明了SE‐EBG‐RA可采用不同数量的单元。还表明,短路版本本质上是四分之一波长天线,而开路版本则是半波长天线。因此,不同于[4]中使用的 $\beta l = \pi/2$,我们可以将 $\beta l = \pi/4$ 代入(1),并以类似方式求得短路版本的 $f_r$。通过对方程的推导可知,只要将 n=4代替开路情况下的2,(1)至(4)可被重复使用。需要注意的是,对于图1所示的两个单元结构,m=2。(1)至(4)为设计者提供了一组新的相对精确的闭式方程,可简化图1中双单元短路型SE‐EBG‐RA的设计流程。
需要注意的是,(4)及上述说明是专门为短路版本(未包含在[4]中)提出的,尽管与[4]中的方程类似,但本文首次给出了这些内容。此外,本研究补充并推广了[4]中的电路模型,因为先前的模型仅适用于开路版本且仅包含三个单元(m=3)。相比之下,在本版本中,m 可在[13]所述范围内任意选择。
3. 基于电路模型的设计流程
如果我们将所提出的模型应用于图1(a),同时考虑图1(c)中的结构参数,$f_r = 5.53$ GHz。该结果与HFSS仿真得到的 $f_r = 5.37$ GHz非常接近(Δ ∼ 3%),表明了电路模型的准确性。这种准确性在开路型天线版本的[4]中也得到了验证。
然而在实际中,使用过孔更容易实现图1(a)中的短路板。因此,如图1(b)所示,用两个过孔替代了金属板。
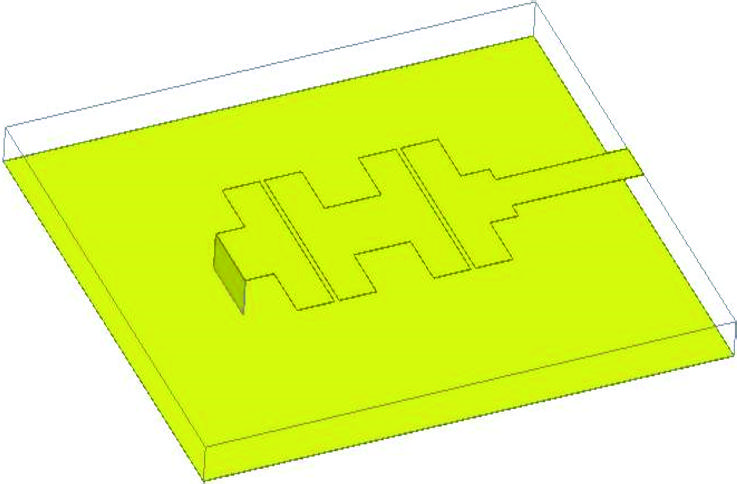
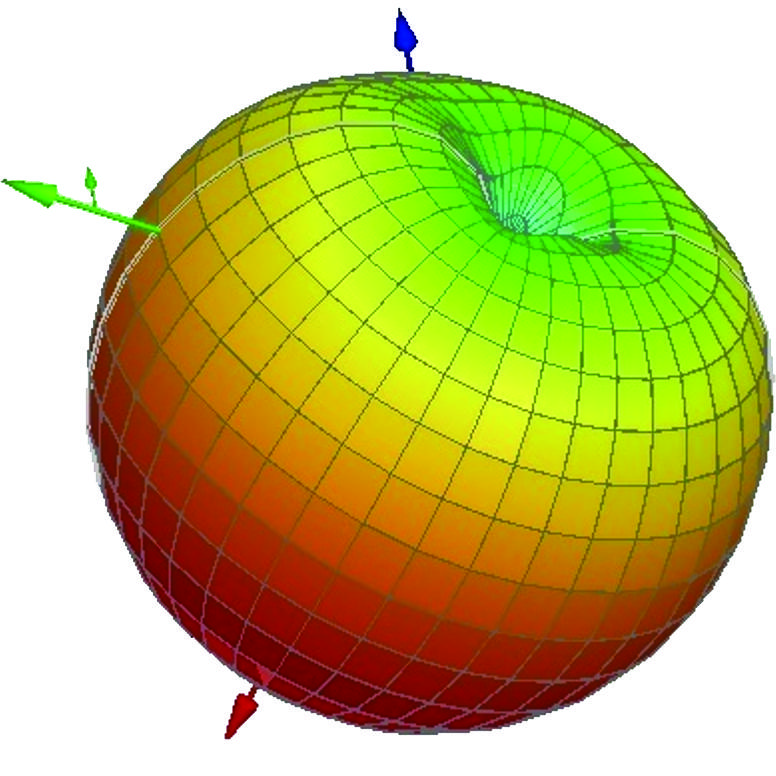
表1比较了双过孔和短路板版本通过模型和HFSS仿真获得的天线特性。可以看出,用过孔替代金属板后,在 $f_r$ 到 $f_r = 6.38$ GHz范围内 ∼19%增加,此时 $\eta_{\text{HFSS}}$ 为85%。图2还显示了双过孔版本的辐射方向图,表明该方向图为宽边辐射,且后向辐射非常小。
19%的频率偏移是相当正常的,因为两个过孔无法完全模拟短路板的相同效果,因此天线在过孔周围仍保留了一些开路特性,从而导致频率偏移。尽管存在这种偏移,该设计仍刻意基于过孔,以使其与标准PCB工艺兼容。此外,采用RO4350B($\varepsilon_r = 3.66$;$\tan\delta = 0.004$)也是为了满足印刷电路板制造的要求,因为这种基板被视为FR4的低损耗配对材料,因此受到大批量制造商的青睐。
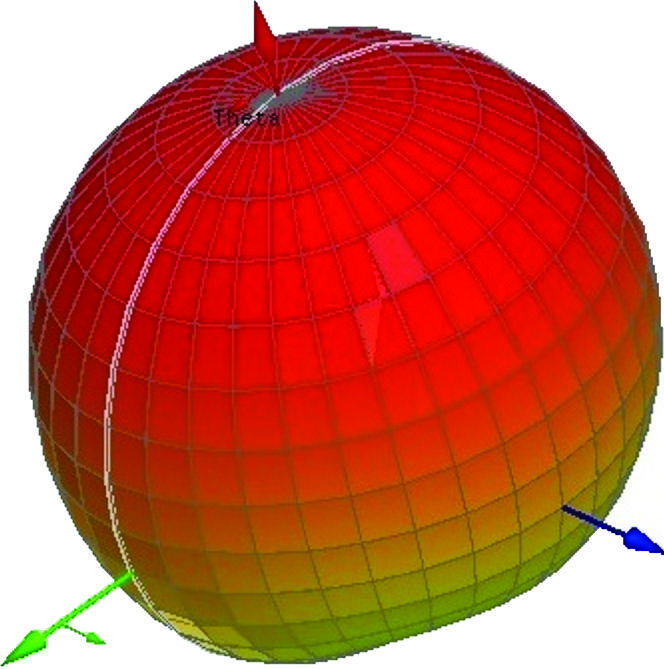
需要注意的是,图1(a)中的天线首次引入了厚金属版本(即在高介电常数基板上具有高宽高比间隙的结构),该结构在[13]中被称为SC SE‐EBG‐RA。相反,所提出的设计采用细迹线(类似于[14, 20]中的天线版本),用过孔代替短路板(便于制造),基于理想的低介电常数材料,并保持了[13]中报道的相对较高的效率。图3展示了图1(b)中天线在应用变压器之前(见点A)和之后(见点B)的输入阻抗曲线。可以看出,点A处的特性符合并联RLC模型,而变压器在6.38 GHz的工作频率附近将模型转变为串联形式。
4. WCM在SC SE‐EBG‐RA中的应用
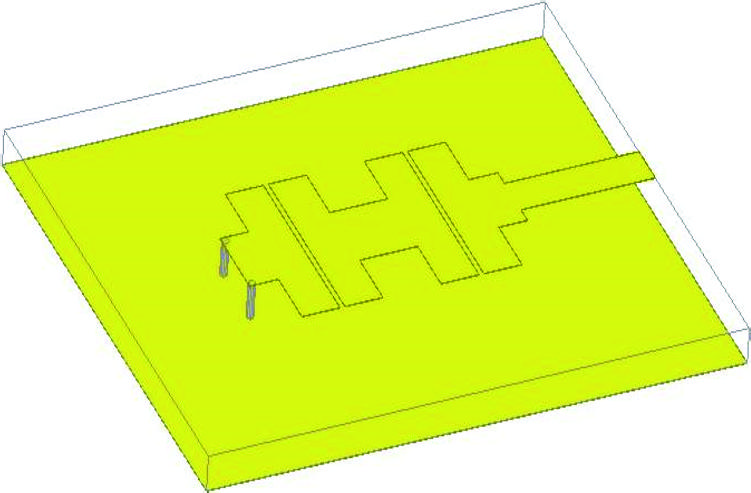
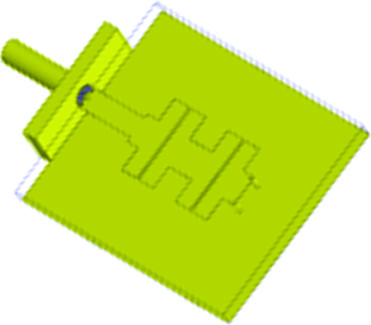
在本节中,一个矩形寄生单元在HFSS中被仔细建模,并放置在第3节设计的天线上方。图1(b)中的设计具有 XY尺寸(单位为毫米);因此,罩体将采用相同的横向尺寸。然而,在选择罩体高度时,一些重要的需要考虑一些因素。从根本上讲,在惠勒罩法(WCM)中,罩体尺寸必须在电学上足够小,以防止罩体内激发谐振模式,否则该罩体可能充当矩形腔体[21]。另一方面,罩体又应足够大,确保其任何部分都不会干扰天线的近场,需注意这些近场可能从天线相位中心延伸至 ∼λ/3[22],或粗略地说,从天线物理中心算起。当罩体高度为15毫米时,该罩体类似于一个矩形腔体谐振器,其 XYZ‐尺寸为 28 × 24 × 15(单位:毫米)。相关教科书公式[23]给出此类谐振器主模TE101的截止频率($f_c$)为11.34 GHz,这一数值远离 $f_r$,较为理想。
值得一提的是,在[13]中已从理论上证明,SC SE‐EBG‐RA本质上是一个四分之一波长短截谐振器,始终遵循并联RLC模型。这一特性也可从图3中点A的阻抗推断得出。然而,当应用变压器时(如图3所示),阻抗将转变为近似串联RLC形式(图1(b)中的点B),这为使用WCM提供了依据。因此,在[13]中针对一个已实现的厚金属SC SE‐EBG‐RA原型,通过 λ/4变压器匹配,实际的WCM对效率进行了准确估计。
 中天线在6.38 GHz下的二维和三维辐射方向图)
中天线在6.38 GHz下的二维和三维辐射方向图)
图4显示了一个综合HFSS模型,该模型精确模拟了典型的SMA连接器、一段短同轴电缆、帽(图4(b))以及图1(b)中的天线。连接器和电缆的建模内导体直径为0.5毫米,外导体直径为2.4毫米。考虑到 $\varepsilon_r = 3.1$,与某些商用连接器类似,并应用相关方程,$Z_0 = (60 / 3.1^{1/2}) \ln (2.4 / 0.5)$ [23] 得到53.45Ω。在同轴电缆的起始位置设置一个波端口以激励结构,HFSS计算出的 $Z_0$ 令人满意地达到了53.50Ω。在图4(c)中,输入阻抗($Z_{\text{in}} = R_{\text{in}} + jX_{\text{in}}$)是在λ/4变压器的起始位置(图4(a)中的点A)计算的;也就是说,连接器和电缆的影响被建模后去嵌入。因此,$f_r$ 从图1(b)中的6.38 GHz略微偏移到图4(c)中的6.47 GHz。该策略有助于模拟使用WCM进行实际测量时发生的情况。
没有帽时,$R_{\text{in}} = 50\Omega$,而当帽安装上时,$R_{\text{in}} = 10.5\Omega$。因此,$\eta_{\text{wc}} = (50\Omega - 10.5\Omega)/50\Omega = 79\%$。然而,当帽被放置时,$f_r$ 不再为6.47 GHz,而是略微下降至6.40 GHz。因此,可以在这一新频率(即6.5Ω)下重新读取 $R_{\text{in}}$,结果为 $\eta_{\text{wc}} = 87\%$。由于该频率偏移仅为 ∼1%,因此更合理的方式是取6.5Ω和10.5Ω(8.5Ω)之间的平均值,并结合WCM使用。在这种情况下,$\eta_{\text{wc}} = (50\Omega - 8.5\Omega)/50\Omega = 83\%$,仅比85%低2.5%($\eta_{\text{HFSS}}$)。
$\eta_{\text{HFSS}}$ 由HFSS内置方法独立计算,根据HFSS手册,该方法是辐射功率(在包围结构的辐射边界盒上积分)与输入实功率之比。值得注意的是,在[13]中,测得的OC SE‐EBG‐RA原型的 $\eta_{\text{wc}}$ 同样比 $\eta_{\text{HFSS}}$ 低7%。这一差异归因于众所周知的现象,即HFSS计算的效率通常略高于实际值。
 中点A(并联RLC模型)和点B(串联RLC模型)处的HFSS仿真输入阻抗)
中点A(并联RLC模型)和点B(串联RLC模型)处的HFSS仿真输入阻抗)
 天线和 (b) 天线上的寄生单元的详细电磁模型,以及 (a) 在有和没有寄生单元情况下的模拟 $Z_{\text{in}}(\Omega)$)
天线和 (b) 天线上的寄生单元的详细电磁模型,以及 (a) 在有和没有寄生单元情况下的模拟 $Z_{\text{in}}(\Omega)$)
5. 电磁模型的另一种验证方法
另一个增加图4中仿真结果可信度并消除原型制作需求的考虑是,在没有天线的情况下对电缆和SMA连接器进行数值评估。图5显示了在HFSS中的一个电磁模型,该模型精确地模拟了一个包含连接器、电缆以及一小段 50Ω微带线的二端口网络。如图6所示,相应的 S‐参数 证实该网络运行良好,这意味着几乎所有的功率都如预期地从端口1传输到端口2。该技术确保了激励源准确性的可靠性。

 和 |S21 |(dB);包含不连续性和SMA连接器的影响)
和 |S21 |(dB);包含不连续性和SMA连接器的影响)
端口处的波和互连的可靠建模,因此(从一个新的角度)验证了图4中的电磁模型。值得一提的是,本文中的验证方法完全基于仿真。在第3节中,HFSS和电路模型计算的谐振频率吻合良好(Δ < 2.9%)。此外,在第4节中,HFSS与模拟 WC方法计算的效率也高度一致(Δ < 2.5%)。本节中的分析也是对天线馈电部分的第三次验证尝试。此类基于仿真的方法适用于小型天线,考虑到结构的电尺寸较小。在这种情况下,整个结构(包括寄生单元)仅为 0.60λ × 0.52λ × 0.32λ。对于如此小的电磁模型,使用低成本计算机即可轻松完成仿真;然而,若模型较大(例如阵列天线),则原型制作与测量不可避免。
6. 极度截断的 SC SE‐EBG‐RA
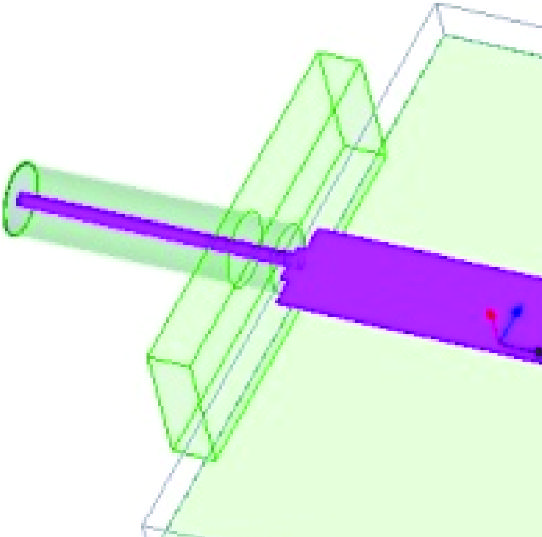
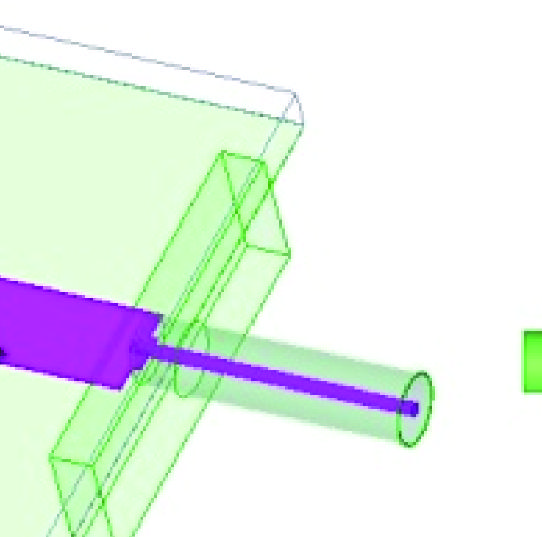
最后的研究是探讨图4(a)所示的短路自激电磁带隙谐振天线对截断的敏感性,以及通过减小接地板尺寸实现进一步小型化的可能性。如图7所示,为了节省占用面积,由于图4(a)中点A处的边缘阻抗为 ∼60Ω(接近 50Ω),因此去除了λ/4变压器。接地板也被截断至16 mm × 14 mm。结构细节如图7所示。可以看到,仿真中仍然包含了一段同轴电缆和SMA。
表2比较了图4(a)中截断版本与原始天线的特性。有趣的是,观察到 η有所改善,且天线电尺寸显著降低。另一个观察结果是,尽管天线经历了严重的截断,谐振频率的偏移仅为1.7%。
正如预期,实现增益已降至4.37dBi(由于电尺寸占用面积更小);尽管如此,对于如此小的电尺寸占用面积而言,该增益仍然显著。此外,相应的辐射方向图如图8所示,表明辐射方向图在截断情况下具有合理的稳定性(注意峰值略微向连接器侧移动)。良好的宽边辐射方向图表明连接器和电缆的寄生效应可以忽略不计。此外,图9对比了截断版本与原始版本的|S11 |(dB)随频率的变化情况,显示匹配质量得以保持,带宽从1.9%提升至3.3%,实现了73%的提升。
 中SC SE‐EBG‐RA的截断版本)
中SC SE‐EBG‐RA的截断版本)
7. 结论
本文介绍了一种由所提出的电路模型引导的、用于小型天线的快速且精确的设计流程。所谓的短路型 SE‐EBG‐RA首先通过该模型进行设计,随后进行演示基于仿真的惠勒罩 (WC) 测量。通过比较 WC 方法与 HFSS 内置方法计算的效率,结果表明两者在估计值上仅有 2.5% 的差异。尽管该研究完全基于数值分析,但对连接器和惠勒罩进行的详细建模足以确保结果的可信度。最终天线设计证明对地板截断具有很强的鲁棒性,呈现出良好的宽边辐射方向图,尺寸小至 0.34λ × 0.30λ × 0.03λ。同时表现出 93% 效率和 4.37dBi 实现增益,以及3.3%的可观带宽。为了使所研究的天线适用于 sub‐6 GHz商业应用,设计使其工作频率接近 5.8GHz免许可频段,并符合标准PCB工艺。
| 表2:截断对SC SE‐EBG‐RA(2通孔)的影响;Δ表示f r的变化量除以非截断情况下的f r;两种情况下均对连接器和电缆进行了精确建模;Gr表示实现增益。 |
|---|
| fr(吉赫兹) |
| 非截断 (图4(a)) |
| 截断 (图7) |
 ;将图7中的截断天线与图4(a)中的非截断版本进行比较)
;将图7中的截断天线与图4(a)中的非截断版本进行比较)





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








