时间常数法

最新推荐文章于 2024-03-05 20:17:10 发布

原创最新推荐文章于 2024-03-05 20:17:10 发布 · 5k 阅读

11 ·

CC 4.0 BY-SA版权

analog 专栏收录该内容

8 篇文章

订阅专栏

对于一个包含多个电容、电感的网络，用KVL或者KCL去硬算它的传函是很困难的。或者说对手工计算很不友好。同时，KVL和KCL不能提供对电路的直观理解（insight）。对于复杂网络，时间常数法更加直观和方便。

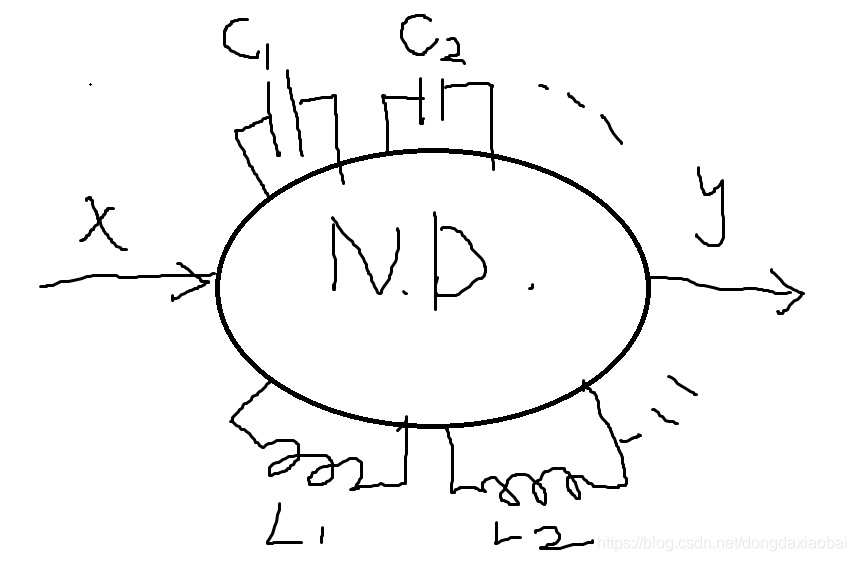现在考虑这样一个网络，输入为x，输出为y。网络包含N个抗性元件（电容C1,C2,C3……电感L1,L2,L3……）。则该网络传函为如下形式 $H(s)=\frac{a_0+a_1s+a_2s^2+\cdots+a_Ms^M}{1+b_1s+b_2s^2+\cdots +b_Ns^N}$ （1）

注：由于电路只包含N个抗性元件，对应有N个极点，所以分母有N项。分子对应M个零点。零点数量和电路节点选取有关。

下面考虑 $H(s)$ 中各个系数的求法。首先注意到，电路中的 $s$ 项不是凭空产生的，每一个 $s$ 必然是由一个 $C$ 或者 $L$ 引入的。这就是时间常数法的根本来源。

1、 $a_0$ 对应直流增益。在式子中，如果所有的 $s=0$ ，那么意味着 $H(s)=a_0$ 。 $s=0$ 是什么含义呢？所有的电容为开路，所有电感为短路。也可以看成，所有 $C$ 或者 $L$ 等于0。

2、 $b_1$ 对应所有的一次项系数之和。而每个一次项系数是怎么产生的呢？考虑某个电容 $C_i$ ，b1中必能找到与之对应项 $sC_i$ 。那么其他项就需要为0。也就是说，所有 $C$ 或者 $L$ 等于0时，从 $C_i$ 两端看进去的电阻，对应 $C_i$ 项的系数。称该电阻为 $R_{i}^{0}$ ，于是得到 $\tau _{i}^{0}=R_{i}^{0}C_i$ ，即 $C_i$ 的时间常数。于是有

$b_1=\sum_{i=1}^{N}\tau_{i}^{0}=\sum_{i=1}^{N}R_{i}^{0}C_i$ （2）

注：对于电感，时间常数为 $\frac{L_i}{R_{i}^{0}}$ 。由于电路中一般用不到电感，所以以下主要都考虑电容的形式。涉及电感类似替换即可。

3、 $a_1=\sum_{i=1}^{N}\tau_{i}^{0}H^i=\sum_{i=1}^{N}R_{i}^{0}C_iH^i$

$H^i$ 这一项什么意思呢？这一项表示 $C_i$ 为无穷大，即短路时电路的传函。（如果是 $L_i$ ，对应开路）。不难理解这种方法的用意，因为分子中的一次项也不会凭空产生，电路中 $C_i$ 无穷大时提取出了分子的对应项系数。由于分母上已经有了相应的时间常数，所以 $H^i$ 要乘上对应的时间常数。

4、 $b_2=\sum_{i,j}^{1\leqslant i<j\leqslant N}\tau_{i}^{0}\tau_{j}^{i}=\sum_{i=1}^{N}R_{i}^{0}C_iR_{j}^{i}C_j$

类似一次项的求解，每个二次项都包含两个电容的乘积。为了找到相应的系数，在计算某两个电容 $C_i,C_j$ 对应的系数时把电路先退化为二阶系统，即令电路中其他电容都等于0（开路）。而后令 $C_i$ 无穷大（短路），对应提取出此时 $C_j$ 两端看进网络的电阻。得到时间常数 $\tau_{i}^{j}$ 。再乘以 $C_i$ 的开路时间常数。

为什么这么做呢？因为计算二次项时，我们可以这样看，分母= $1+(C_1R_{1}^{0}s+C_1R_{1}^{0}\sum_{1<j\leqslant N} \beta_j^1C_js^2)+(C_2R_{2}^{0}s+C_2R_{2}^{0}\sum_{2<j\leqslant N} \beta_j^2C_js^2)+\cdots$