前言
在数学及工程上经常需要用到Newton-Leibniz积分公式:
∫
a
b
f
(
x
)
d
x
=
F
(
b
)
−
F
(
a
)
\int_a^b f(x)dx=F(b)-F(a)
∫abf(x)dx=F(b)−F(a)
但存在一些原因导致我们无法使用:
- 原函数无法用初等函数表示,如sin(1/x)。
- 原函数过于复杂不便于计算。
- 被积函数是由实验测量得到,没有具体的表达式。
所以就需要用数值的方法进行替代。根据采样间隔是否相等,可以分为:
- 等间距的 牛顿-柯特斯公式
- 不等间距的 高斯公式
另外,不同于其他同类型的文章,本文还提供高维的数值积分公式,包括三角区域的二重积分、四面体区域的三重积分。
一维积分公式
参考 数值分析——求积公式
牛顿-柯特斯(Newton-Cotes)公式
I = ∫ a b f ( x ) d x I=\int_a^b f(x)dx I=∫abf(x)dx
| n | 近似公式 | 截断误差 | 精度 | 备注 |
|---|---|---|---|---|
| 1 | I ≈ b − a 2 ( f 0 + f 1 ) I\approx\frac{b-a}{2}(f_0+f_1) I≈2b−a(f0+f1) | − ( b − a ) 3 12 f ′ ′ ( ξ ) -\frac{(b-a)^3}{12}f''(\xi) −12(b−a)3f′′(ξ) | 1 | 梯形公式 |
| 2 | I ≈ b − a 6 ( f 0 + 4 f 1 + f 2 ) I\approx\frac{b-a}{6}(f_0+4f_1+f_2) I≈6b−a(f0+4f1+f2) | − ( b − a ) 5 2880 f ( 4 ) ( ξ ) -\frac{(b-a)^5}{2880}f^{(4)}(\xi) −2880(b−a)5f(4)(ξ) | 3 | 辛普森(Simpson)公式 |
| 3 | I ≈ b − a 8 ( f 0 + 3 f 1 + 3 f 2 + f 3 ) I\approx\frac{b-a}{8}(f_0+3f_1+3f_2+f_3) I≈8b−a(f0+3f1+3f2+f3) | − ( b − a ) 5 6480 f ( 4 ) ( ξ ) -\frac{(b-a)^5}{6480}f^{(4)}(\xi) −6480(b−a)5f(4)(ξ) | 3 | 辛普森(Simpson)3/8公式 |
| 4 | I ≈ b − a 90 ( 7 f 0 + 32 f 1 + 12 f 2 + 32 f 3 + 7 f 4 ) I\approx\frac{b-a}{90}(7f_0+32f_1+12f_2+32f_3+7f_4) I≈90b−a(7f0+32f1+12f2+32f3+7f4) | − ( b − a ) 7 1935360 f ( 6 ) ( ξ ) -\frac{(b-a)^7}{1935360}f^{(6)}(\xi) −1935360(b−a)7f(6)(ξ) | 5 | 柯特斯(Cotes)公式、布尔(Boole)法则 |
| 5 | I ≈ b − a 288 ( 19 f 0 + 75 f 1 + 50 f 2 + 50 f 3 + 75 f 4 + 19 f 5 ) I\approx\frac{b-a}{288}(19f_0+75f_1+50f_2+50f_3+75f_4+19f_5) I≈288b−a(19f0+75f1+50f2+50f3+75f4+19f5) | − 11 ( b − a ) 7 37800000 f ( 6 ) ( ξ ) -\frac{11(b-a)^7}{37800000}f^{(6)}(\xi) −3780000011(b−a)7f(6)(ξ) | 5 | |
| 6 | I ≈ b − a 840 ( 41 f 0 + 216 f 1 + 27 f 2 + 272 f 3 + 27 f 4 + 216 f 5 + 41 f 6 ) I\approx\frac{b-a}{840}(41f_0+216f_1+27f_2+272f_3+27f_4+216f_5+41f_6) I≈840b−a(41f0+216f1+27f2+272f3+27f4+216f5+41f6) | − 11 ( b − a ) 9 1567641600 f ( 8 ) ( ξ ) -\frac{11(b-a)^9}{1567641600}f^{(8)}(\xi) −156764160011(b−a)9f(8)(ξ) | 7 | |
| 7 | I ≈ b − a 17280 ( 751 f 0 + 3577 f 1 + 1323 f 2 + 2989 f 3 + 2989 f 4 + 1323 f 5 + 3577 f 6 + 751 f 7 ) I\approx\frac{b-a}{17280}(751 f_0+3577 f_1+1323 f_2+2989 f_3+2989 f_4+1323 f_5+3577 f_6+751 f_7) I≈17280b−a(751f0+3577f1+1323f2+2989f3+2989f4+1323f5+3577f6+751f7) | − 167 ( b − a ) 9 26924691200 f ( 8 ) ( ξ ) -\frac{167(b-a)^9}{26924691200}f^{(8)}(\xi) −26924691200167(b−a)9f(8)(ξ) | 7 | |
| 8 | I ≈ b − a 28350 ( 989 f 0 + 5888 f 1 − 928 f 2 + 10496 f 3 − 4540 f 4 + 10496 f 5 − 928 f 6 + 5888 f 7 + 989 f 8 ) I\approx\frac{b-a}{28350}(989 f_0+5888 f_1-928 f_2+10496 f_3-4540 f_4+10496 f_5-928 f_6+5888 f_7+989 f_8) I≈28350b−a(989f0+5888f1−928f2+10496f3−4540f4+10496f5−928f6+5888f7+989f8) | − 37 ( b − a ) 11 62783697715200 f ( 10 ) ( ξ ) -\frac{37(b-a)^{11}}{62783697715200}f^{(10)}(\xi) −6278369771520037(b−a)11f(10)(ξ) | 9 |
这里
f
k
=
f
(
a
+
k
n
(
b
−
a
)
)
,
a
≤
ξ
≤
b
f_k=f(a+\frac{k}{n}(b-a)),a \le ξ \le b
fk=f(a+nk(b−a)),a≤ξ≤b。
如果
f
(
x
)
f(x)
f(x)是多项式,且最高次数不高于精度值,那截断误差为0,近似公式变成恒等公式,即
≈
\approx
≈ 可替换为
=
=
=。
辛普森(Simpson)公式
如果
f
(
x
)
f(x)
f(x)是不高于3次的多项式,那有
∫
a
b
f
(
x
)
d
x
=
b
−
a
6
[
f
(
a
)
+
4
f
(
a
+
b
2
)
+
f
(
b
)
]
\int_a^b f(x)dx=\frac{b-a}{6}[f(a)+4f(\frac{a+b}{2})+f(b)]
∫abf(x)dx=6b−a[f(a)+4f(2a+b)+f(b)]
对于常见的几何体,体积公式为
V
=
h
6
(
S
上底面
+
4
S
中截面
+
S
下底面
)
V=\frac{h}{6}(S_{上底面}+4S_{中截面}+S_{下底面})
V=6h(S上底面+4S中截面+S下底面)。例如:
V
柱体
=
h
6
(
S
底面
+
4
×
S
底面
+
S
底面
)
=
h
S
底面
V_{柱体}=\frac{h}{6}(S_{底面}+4\times S_{底面}+S_{底面})=hS_{底面}
V柱体=6h(S底面+4×S底面+S底面)=hS底面
V
锥体
=
h
6
(
0
+
4
×
(
S
底面
/
4
)
+
S
底面
)
=
h
3
S
底面
V_{锥体}=\frac{h}{6}(0+4\times (S_{底面}/4)+S_{底面})=\frac{h}{3}S_{底面}
V锥体=6h(0+4×(S底面/4)+S底面)=3hS底面
V
台体
=
h
6
(
S
上底面
+
4
S
上底面
S
下底面
+
S
下底面
)
V_{台体}=\frac{h}{6}(S_{上底面}+4 \sqrt{S_{上底面}S_{下底面}}+S_{下底面})
V台体=6h(S上底面+4S上底面S下底面+S下底面)
V
球体
=
2
r
6
(
0
+
4
×
π
r
2
+
0
)
=
4
r
3
3
V_{球体}=\frac{2r}{6}(0+4\times\pi r^2+0)=\frac{4r^3}{3}
V球体=62r(0+4×πr2+0)=34r3
复化公式
高阶Newton-Cotes公式会出现数值不稳定。而低阶Newton-Cotes公式又不能满足精度要求。为了提高精度可将积分区间分成若干子区间,在每个子区间上用低阶求积公式计算然后相加的求积公式称为复化求积公式。
∫
a
b
f
(
x
)
d
x
=
b
−
a
6
n
(
f
0
+
4
f
1
+
2
f
2
+
.
.
.
+
2
f
2
k
+
4
f
2
k
+
1
+
.
.
.
+
4
f
2
n
−
1
+
f
2
n
)
\int_a^b f(x)dx=\frac{b-a}{6n}(f_0+4f_1+2f_2+...+2f_{2k}+4f_{2k+1}+...+4f_{2n-1}+f_{2n})
∫abf(x)dx=6nb−a(f0+4f1+2f2+...+2f2k+4f2k+1+...+4f2n−1+f2n)
高斯型求积公式
若n个节点的插值型求积公式具有2n-1次代数精度,则称为Gauss型求积公式,是代数精度最高的求积公式。表示如下:
∫
a
b
ρ
(
x
)
f
(
x
)
d
x
≈
∑
k
=
1
n
A
k
f
(
x
k
)
\int_a^b\rho(x) f(x)dx \approx \sum_{k=1}^n A_kf(x_k)
∫abρ(x)f(x)dx≈k=1∑nAkf(xk)
本节主要参考 数值分析——求积公式
高斯-勒让德(Gauss-Legendre)求积公式
∫
−
1
1
f
(
x
)
d
x
≈
∑
k
=
1
n
A
k
f
(
x
k
)
\int_{-1}^1 f(x)dx \approx \sum_{k=1}^n A_kf(x_k)
∫−11f(x)dx≈k=1∑nAkf(xk)
x
k
x_k
xk是勒让德多项式
L
n
(
x
)
=
1
2
n
n
!
d
n
d
x
n
(
x
2
−
1
)
n
L_n(x)=\frac{1}{2^n n!}\frac{d^n}{dx^n}(x^2-1)^n
Ln(x)=2nn!1dxndn(x2−1)n 的零点,
A
k
=
2
(
1
−
x
k
2
)
[
L
n
′
(
x
k
)
]
2
A_k=\frac{2}{(1-x_k^2)[L'_n(x_k)]^2}
Ak=(1−xk2)[Ln′(xk)]22
| n | L n ( x ) L_n(x) Ln(x) | x k x_k xk | A k A_k Ak |
|---|---|---|---|
| 1 | x x x | 0 | 2 |
| 2 | ( 3 x 2 − 1 ) / 2 (3x^2-1)/2 (3x2−1)/2 | ± 3 / 3 = ± 0.5773502692 \pm\sqrt{3}/3=\pm0.577 350 269 2 ±3/3=±0.5773502692 | 1 |
| 3 | ( 5 x 3 − 3 x ) / 2 (5x^3 - 3x)/2 (5x3−3x)/2 | 0 ± 15 / 5 = ± 0.7745966692 0\\\pm\sqrt{15}/5=\pm0.774 596 669 2 0±15/5=±0.7745966692 | 8 / 9 = 0.8888888889 5 / 9 = 0.5555555556 8/9=0.888 888 888 9\\5/9=0.555 555 555 6 8/9=0.88888888895/9=0.5555555556 |
| 4 | ( 35 x 4 − 30 x 2 + 3 ) / 8 (35x^4 - 30x^2 + 3)/8 (35x4−30x2+3)/8 | ± ( 15 − 2 30 ) / 35 = ± 0.3399810436 ± ( 15 + 2 30 ) / 35 = ± 0.8611363116 \pm\sqrt{(15-2\sqrt{30})/35}=\pm0.339 981 043 6\\\pm\sqrt{(15+2\sqrt{30})/35}=\pm0.861 136 311 6 ±(15−230)/35=±0.3399810436±(15+230)/35=±0.8611363116 | ( 18 + 30 ) / 36 = 0.6521451549 ( 18 − 30 ) / 36 = 0.3478548451 (18+\sqrt{30})/36=0.652 145 154 9\\(18-\sqrt{30})/36=0.347 854 845 1 (18+30)/36=0.6521451549(18−30)/36=0.3478548451 |
| 5 | ( 63 x 5 − 70 x 3 + 15 x ) / 8 (63x^5 - 70x^3 + 15x)/8 (63x5−70x3+15x)/8 | 0 ± ( 35 − 2 70 ) / 63 = ± 0.538469310 ± ( 35 + 2 70 ) / 63 = ± 0.906179846 0\\\pm\sqrt{(35-2\sqrt{70})/63}=\pm0.538 469 310\\\pm\sqrt{(35+2\sqrt{70})/63}=\pm0.906 179 846 0±(35−270)/63=±0.538469310±(35+270)/63=±0.906179846 | 128 / 225 = 0.5688888889 ( 322 + 13 70 ) / 900 = 0.4786286705 ( 322 − 13 70 ) / 900 = 0.2369268851 128/225=0.568 888 888 9\\(322+13\sqrt{70})/900=0.478 628 670 5\\(322-13\sqrt{70})/900=0.236 926 885 1 128/225=0.5688888889(322+1370)/900=0.4786286705(322−1370)/900=0.2369268851 |
| 6 | ( 231 x 6 − 315 x 4 + 105 x 2 − 5 ) / 16 (231 x^6 - 315x^4 + 105x^2 - 5)/16 (231x6−315x4+105x2−5)/16 | ± 0.2386191861 ± 0.6612093865 ± 0.9324695142 \pm0.238 619 186 1\\\pm0.661 209 386 5\\\pm0.932 469 514 2 ±0.2386191861±0.6612093865±0.9324695142 | 0.4679139346 0.3607615730 0.1713244924 0.467 913 934 6\\0.360 761 573 0\\0.171 324 492 4 0.46791393460.36076157300.1713244924 |
| 7 | ( 429 x 7 − 693 x 5 + 315 x 3 − 35 x ) / 16 (429x^7 - 693x^5 + 315x^3 - 35x)/16 (429x7−693x5+315x3−35x)/16 | 0 ± 0.4058451514 ± 0.7415311856 ± 0.9491079123 0\\\pm 0.405 845 151 4\\\pm 0.741 531 185 6\\\pm 0.949 107 912 3 0±0.4058451514±0.7415311856±0.9491079123 | 0.4179591837 0.3818300505 0.2797053915 0.1294849662 0.417 959 183 7\\0.381 830 050 5\\0.279 705 391 5\\0.129 484 966 2 0.41795918370.38183005050.27970539150.1294849662 |
| 8 | ( 6435 x 8 − 12012 x 6 + 6930 x 4 − 1260 x 2 + 35 ) / 128 (6435x^8 - 12012x^6 + 6930x^4 - 1260x^2 + 35)/128 (6435x8−12012x6+6930x4−1260x2+35)/128 | ± 0.1834346425 ± 0.5255324099 ± 0.7966664774 ± 0.9602898565 \pm 0.183 434 642 5\\\pm 0.525 532 409 9\\\pm 0.796 666 477 4\\\pm 0.960 289 856 5 ±0.1834346425±0.5255324099±0.7966664774±0.9602898565 | 0.3626837834 0.3137066459 0.2223810345 0.1012285363 0.362 683 783 4\\0.313 706 645 9\\0.222 381 034 5\\0.101 228 536 3 0.36268378340.31370664590.22238103450.1012285363 |
高斯-拉盖尔(Gauss-Laguerre)求积公式
∫
0
+
∞
e
−
x
f
(
x
)
d
x
≈
∑
k
=
1
n
A
k
f
(
x
k
)
\int_0^{+\infty} e^{-x} f(x)dx \approx \sum_{k=1}^n A_kf(x_k)
∫0+∞e−xf(x)dx≈k=1∑nAkf(xk)
x
k
x_k
xk是拉盖尔多项式
U
n
=
e
x
d
n
d
x
n
(
x
n
e
−
x
)
U_n=e^x\frac{d^n}{dx^n}(x^ne^{-x})
Un=exdxndn(xne−x) 的零点,
A
k
=
(
n
!
)
2
x
k
[
U
x
′
(
x
k
)
]
2
A_k=\frac{(n!)^2}{x_k[U'_x(x_k)]^2}
Ak=xk[Ux′(xk)]2(n!)2
| n | U n ( x ) U_n(x) Un(x) | x k x_k xk | A k A_k Ak |
|---|---|---|---|
| 1 | − ( x − 1 ) -(x-1) −(x−1) | 1 | 1 |
| 2 | x 2 − 4 x + 2 x^2-4x+2 x2−4x+2 | 2 − 2 = 0.5857864376 2 + 2 = 3.4142135624 2-\sqrt{2}=0.585 786 437 6\\2+\sqrt{2}=3.414 213 562 4 2−2=0.58578643762+2=3.4142135624 | ( 2 + 2 ) / 4 = 0.8535533906 ( 2 − 2 ) / 4 = 0.1464466094 (2+\sqrt{2})/4=0.853 553 390 6\\(2- \sqrt{2})/4=0.146 446 609 4 (2+2)/4=0.8535533906(2−2)/4=0.1464466094 |
| 3 | − ( x 3 − 9 x 2 + 18 x − 6 ) -(x^3-9x^2+18x-6) −(x3−9x2+18x−6) | 0.4157745568 2.2942803603 6.2899450829 0.415 774 556 8\\2.294 280 360 3\\6.289 945 082 9 0.41577455682.29428036036.2899450829 | 0.7110930099 0.2785177336 0.0103892565 0.711 093 009 9\\0.278 517 733 6\\0.010 389 256 5 0.71109300990.27851773360.0103892565 |
| 4 | x 4 − 16 x 3 + 72 x 2 − 96 x + 24 x^4-16x^3+72x^2-96x+24 x4−16x3+72x2−96x+24 | 0.3225476896 1.7457611012 4.5366202969 9.3950709123 0.322 547 689 6\\1.745 761 101 2\\4.536 620 296 9\\9.395 070 912 3 0.32254768961.74576110124.53662029699.3950709123 | 0.6031541043 0.3574186924 0.0388879085 0.0005392947 0.603 154 104 3\\0.357 418 692 4\\0.038 887 908 5\\0.000 539 294 7 0.60315410430.35741869240.03888790850.0005392947 |
| 5 | − ( x 5 − 25 x 4 + 200 x 3 − 600 x 2 + 600 x − 120 ) -(x^5-25x^4+200x^3-600x^2+600x-120) −(x5−25x4+200x3−600x2+600x−120) | 0.2635603197 1.4134030591 3.5964257710 7.0858100059 12.6408008443 0.263 560 319 7\\1.413 403 059 1\\3.596 425 771 0\\7.085 810 005 9\\12.640 800 844 3 0.26356031971.41340305913.59642577107.085810005912.6408008443 | 0.5217556106 0.3986668111 0.0759424497 0.0036117587 0.0000233700 0.521 755 610 6\\0.398 666 811 1\\0.075 942 449 7\\0.003 611 758 7\\0.000 023 370 0 0.52175561060.39866681110.07594244970.00361175870.0000233700 |
| 6 | x 6 − 36 x 5 + 450 x 4 − 2400 x 3 + 5400 x 2 − 4320 x + 720 x^6-36x^5+450x^4-2400x^3+5400x^2-4320x+720 x6−36x5+450x4−2400x3+5400x2−4320x+720 | 0.2228466042 1.1889321017 2.9927363261 5.7751435691 9.8374674184 15.9828739806 0.222 846 604 2\\1.188 932 101 7\\2.992 736 326 1\\5.775 143 569 1\\9.837 467 418 4\\15.982 873 980 6 0.22284660421.18893210172.99273632615.77514356919.837467418415.9828739806 | 0.4589646739 0.4170008308 0.1133733821 0.0103991975 0.0002610172 0.0000008985 0.458 964 673 9\\0.417 000 830 8\\0.113 373 382 1\\0.010 399 197 5\\0.000 261 017 2\\0.000 000 898 5 0.45896467390.41700083080.11337338210.01039919750.00026101720.0000008985 |
高斯-埃尔米特(Gauss-Hermite)求积公式
∫
−
∞
+
∞
e
−
x
2
f
(
x
)
d
x
≈
∑
k
=
1
n
A
k
f
(
x
k
)
\int_{-\infty}^{+\infty} e^{-x^2} f(x)dx \approx \sum_{k=1}^n A_kf(x_k)
∫−∞+∞e−x2f(x)dx≈k=1∑nAkf(xk)
x
k
x_k
xk是埃尔米特多项式
H
n
=
(
−
1
)
n
e
x
2
d
n
d
x
n
(
e
−
x
2
)
H_n=(-1)^ne^{x^2}\frac{d^n}{dx^n}(e^{-x^2})
Hn=(−1)nex2dxndn(e−x2) 的零点,
A
k
=
2
n
+
1
n
!
π
[
H
x
′
(
x
k
)
]
2
A_k=\frac{2^{n+1}n!\sqrt{\pi}}{[H'_x(x_k)]^2}
Ak=[Hx′(xk)]22n+1n!π
| n | H n ( x ) H_n(x) Hn(x) | x k x_k xk | A k A_k Ak |
|---|---|---|---|
| 1 | 2 x 2x 2x | 0 | π = 1.7724538509 \sqrt{\pi}=1.772 453 850 9 π=1.7724538509 |
| 2 | 2 ( 2 x 2 − 1 ) 2(2x^2-1) 2(2x2−1) | ± 2 / 2 = ± 0.7071067812 \pm\sqrt{2}/2=\pm 0.707 106 781 2 ±2/2=±0.7071067812 | π / 2 = 0.8862269255 \sqrt{\pi}/2=0.886 226 925 5 π/2=0.8862269255 |
| 3 | 4 ( 2 x 3 − 3 x ) 4(2x^3-3x) 4(2x3−3x) | 0 ± 6 / 2 = ± 1.2247448714 0\\\pm\sqrt{6}/2=\pm 1.224 744 871 4 0±6/2=±1.2247448714 | 2 π / 3 = 1.1816359006 π / 6 = 0.2954089752 2\sqrt{\pi}/3=1.181 635 900 6\\\sqrt{\pi}/6=0.295 408 975 2 2π/3=1.1816359006π/6=0.2954089752 |
| 4 | 4 ( 4 x 4 − 12 x 2 + 3 ) 4(4x^4-12x^2+3) 4(4x4−12x2+3) | ± ( 3 − 6 ) / 2 = ± 0.5246476233 ± ( 3 + 6 ) / 2 = ± 1.6506801239 \pm\sqrt{(3-\sqrt{6})/2}=\pm0.524 647 623 3\\\pm\sqrt{(3+\sqrt{6})/2}=\pm1.650 680 123 9 ±(3−6)/2=±0.5246476233±(3+6)/2=±1.6506801239 | ( 3 + 6 ) π / 12 = 0.8049140900 ( 3 − 6 ) π / 12 = 0.0813128354 (3+ \sqrt{6})\sqrt{\pi}/12=0.804 914 090 0\\(3 - \sqrt{6})\sqrt{\pi}/12=0.081 312 835 4 (3+6)π/12=0.8049140900(3−6)π/12=0.0813128354 |
| 5 | 8 ( 4 x 5 − 20 x 3 + 15 x ) 8(4x^5-20x^3+15x) 8(4x5−20x3+15x) | 0 ± ( 5 − 10 ) / 2 = ± 0.9585724646 ± ( 5 + 10 ) / 2 = ± 2.0201828705 0\\\pm\sqrt{(5-\sqrt{10})/2}=\pm0.958 572 464 6\\\pm\sqrt{(5+\sqrt{10})/2}=\pm2.020 182 870 5 0±(5−10)/2=±0.9585724646±(5+10)/2=±2.0201828705 | 8 π / 15 = 0.9453087205 ( 7 + 2 10 ) π / 60 = 0.3936193232 ( 7 − 2 10 ) π / 60 = 0.0199532421 8\sqrt{\pi}/15=0.945 308 720 5\\(7+2\sqrt{10})\sqrt{\pi}/60=0.393 619 323 2\\(7-2\sqrt{10})\sqrt{\pi}/60=0.019 953 242 1 8π/15=0.9453087205(7+210)π/60=0.3936193232(7−210)π/60=0.0199532421 |
| 6 | 8 ( 8 x 6 − 60 x 4 + 90 x 2 − 15 ) 8(8x^6-60x^4+90x^2-15) 8(8x6−60x4+90x2−15) | ± 0.4360774119 ± 1.3358490740 ± 2.3506049737 \pm0.436 077 411 9\\\pm1.335 849 074 0\\\pm2.350 604 973 7 ±0.4360774119±1.3358490740±2.3506049737 | 0.7246295952 0.1570673203 0.0045300099 0.724 629 595 2\\0.157 067 320 3\\0.004 530 009 9 0.72462959520.15706732030.0045300099 |
高斯-切比雪夫(Gauss-Chebyshev)求积公式
∫
−
1
1
1
1
−
x
2
f
(
x
)
d
x
≈
∑
k
=
1
n
A
k
f
(
x
k
)
\int_{-1}^{1} \frac{1}{\sqrt{1-x^2}} f(x)dx \approx \sum_{k=1}^n A_kf(x_k)
∫−111−x21f(x)dx≈k=1∑nAkf(xk)
x
k
x_k
xk是第一类切比雪夫多项式
T
n
=
cos
(
n
arccos
(
x
)
)
T_n=\cos(n \arccos(x))
Tn=cos(narccos(x)) 的零点,即
x
k
=
cos
(
2
(
n
−
k
)
+
1
)
π
2
n
,
k
=
1...
n
x_k=\cos \frac{(2(n-k)+1)\pi}{2n},k=1...n
xk=cos2n(2(n−k)+1)π,k=1...n,且有
A
k
=
π
/
n
A_k=\pi/n
Ak=π/n
迭代公式:
T
0
=
1
,
T
1
=
x
,
T
n
=
2
x
T
n
−
1
−
T
n
−
2
T_0=1,T_1=x,T_n=2xT_{n-1}-T_{n-2}
T0=1,T1=x,Tn=2xTn−1−Tn−2
| n | T n T_n Tn | x k x_k xk | A k A_k Ak |
|---|---|---|---|
| 1 | x | 0 | π \pi π |
| 2 | 2 x 2 − 1 2x^2-1 2x2−1 | cos ( 3 π / 4 ) = − 0.70710678 cos ( π / 4 ) = 0.70710678 \cos(3\pi/4)=-0.70710678\\\cos(\pi/4)=0.70710678 cos(3π/4)=−0.70710678cos(π/4)=0.70710678 | π / 2 \pi/2 π/2 |
| 3 | 4 x 3 − 3 x 4x^3-3x 4x3−3x | cos ( 5 π / 6 ) = − 0.86602540 cos ( 3 π / 6 ) = 0 cos ( π / 6 ) = 0.86602540 \cos(5\pi/6)=-0.86602540\\\cos(3\pi/6)=0\\\cos(\pi/6)=0.86602540 cos(5π/6)=−0.86602540cos(3π/6)=0cos(π/6)=0.86602540 | π / 3 \pi/3 π/3 |
| 4 | 8 x 4 − 8 x 2 + 1 8x^4-8x^2+1 8x4−8x2+1 | cos ( 7 π / 8 ) = − 0.92387953 cos ( 5 π / 8 ) = − 0.38268343 cos ( 3 π / 8 ) = 0.38268343 cos ( π / 8 ) = 0.92387953 \cos(7\pi/8)=-0.92387953\\\cos(5\pi/8)=-0.38268343\\\cos(3\pi/8)=0.38268343\\\cos(\pi/8)=0.92387953 cos(7π/8)=−0.92387953cos(5π/8)=−0.38268343cos(3π/8)=0.38268343cos(π/8)=0.92387953 | π / 4 \pi/4 π/4 |
∫
−
1
1
1
−
x
2
f
(
x
)
d
x
≈
∑
k
=
1
n
A
k
f
(
x
k
)
\int_{-1}^{1} \sqrt{1-x^2} f(x)dx \approx \sum_{k=1}^n A_kf(x_k)
∫−111−x2f(x)dx≈k=1∑nAkf(xk)
x
k
x_k
xk是第二类切比雪夫多项式
U
n
=
U_n=
Un= 的零点,即
x
k
=
cos
k
π
n
+
1
,
k
=
1...
n
x_k=\cos \frac{k\pi}{n+1},k=1...n
xk=cosn+1kπ,k=1...n, 且有
A
k
=
π
n
+
1
sin
2
k
π
n
+
1
A_k=\frac{\pi}{n+1}\sin^2\frac{k\pi}{n+1}
Ak=n+1πsin2n+1kπ
迭代公式:
U
0
=
1
,
U
1
=
2
x
,
U
n
=
2
x
U
n
−
1
−
U
n
−
2
U_0=1,U_1=2x,U_n=2xU_{n-1}-U_{n-2}
U0=1,U1=2x,Un=2xUn−1−Un−2
| n | U n U_n Un | x k x_k xk | A k A_k Ak |
|---|---|---|---|
| 1 | 2 x 2x 2x | 0 | π / 2 = 1.5707963268 \pi/2=1.570 796 326 8 π/2=1.5707963268 |
| 2 | 4 x 2 − 1 4x^2-1 4x2−1 | cos ( 2 π / 3 ) = − 0.5 cos ( π / 3 ) = 0.5 \cos(2\pi/3)=-0.5\\\cos(\pi/3)=0.5 cos(2π/3)=−0.5cos(π/3)=0.5 | π / 4 = 0.7853981634 \pi/4=0.785 398 163 4 π/4=0.7853981634 |
| 3 | 8 x 3 − 4 x 8x^3-4x 8x3−4x | cos ( 3 π / 4 ) = − 0.7071067812 cos ( 2 π / 4 ) = 0 cos ( π / 4 ) = 0.7071067812 \cos(3\pi/4)=-0.707 106 781 2\\\cos(2\pi/4)=0\\\cos(\pi/4)=0.707 106 781 2 cos(3π/4)=−0.7071067812cos(2π/4)=0cos(π/4)=0.7071067812 | π / 8 = 0.3926990817 π / 4 = 0.7853981634 π / 8 = 0.3926990817 \pi/8=0.392 699 081 7\\\pi/4=0.785 398 163 4\\\pi/8=0.392 699 081 7 π/8=0.3926990817π/4=0.7853981634π/8=0.3926990817 |
| 4 | 16 x 4 − 12 x 2 + 1 16x^4-12x^2+1 16x4−12x2+1 | cos ( 4 π / 5 ) = − 0.8090169944 cos ( 3 π / 5 ) = − 0.3090169944 cos ( 2 π / 5 ) = 0.3090169944 cos ( π / 5 ) = 0.8090169944 \cos(4\pi/5)=-0.809 016 994 4\\\cos(3\pi/5)=-0.309 016 994 4\\\cos(2\pi/5)=0.309 016 994 4\\\cos(\pi/5)=0.809 016 994 4 cos(4π/5)=−0.8090169944cos(3π/5)=−0.3090169944cos(2π/5)=0.3090169944cos(π/5)=0.8090169944 | 0.2170787134 0.5683194500 0.5683194500 0.2170787134 0.217 078 713 4\\0.568 319 450 0\\0.568 319 450 0\\0.217 078 713 4 0.21707871340.56831945000.56831945000.2170787134 |
数值对比
在本小节的结尾,特地放一段数值积分的对比,让读者了解各公式的准确度。
定积分为
∫
0
8
f
(
x
)
d
x
\int_0^8f(x)dx
∫08f(x)dx,下面牛顿柯特斯公式均采样
x
=
0
,
1
,
.
.
.
,
8
x=0,1,...,8
x=0,1,...,8 共9个点,高斯公式均采样8个点。
| f ( x ) f(x) f(x) | 梯形公式 n = 1 n=1 n=1 | 辛普森公式 n = 2 n=2 n=2 | 柯特斯公式 n = 4 n=4 n=4 | 牛顿柯特斯 n = 8 n=8 n=8 | 高斯勒让德 n = 2 n=2 n=2 | 高斯勒让德 n = 4 n=4 n=4 | 高斯勒让德 n = 8 n=8 n=8 |
|---|---|---|---|---|---|---|---|
| e x e^x ex | -244.287 | -14.7721 | -4.00194 | -0.383593 | 9.77043 | 0.066819 | 0.0000026 |
| 1 x + 1 \frac{1}{x+1} x+11 | -0.076188 | -0.012828 | -0.008348 | -0.004487 | 0.007919 | 0.001007 | 0.0000456 |
| x \sqrt{x} x | 0.193157 | 0.081173 | 0.071288 | 0.059235 | -0.020615 | -0.009287 | -0.0038220 |
通过上表,可以得到结论:
- 越高阶的公式准确度越高,但提高阶数并不一定能快速收敛误差
- 同阶数前提下,高斯勒让德公式的准确度要优于牛顿柯特斯公式
二重积分-三角区域
∬
Δ
f
(
x
,
y
)
d
S
≈
S
Δ
∑
k
=
1
N
A
k
f
(
α
k
,
β
k
,
γ
k
)
\iint_\Delta f(x,y)dS\approx S_\Delta \sum_{k=1}^N A_kf(\alpha_k,\beta_k,\gamma_k)
∬Δf(x,y)dS≈SΔk=1∑NAkf(αk,βk,γk)
其中积分区域为三角形Δ ,其顶点为
p
i
=
(
x
i
,
y
i
)
,
i
=
1
,
2
,
3
p_i=(x_i,y_i), i=1,2,3
pi=(xi,yi),i=1,2,3,并且其面积记为
S
Δ
S_\Delta
SΔ,且有
S
Δ
=
1
2
∣
x
1
y
1
1
x
2
y
2
1
x
3
y
3
1
∣
S_\Delta=\frac{1}{2}\begin{vmatrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{vmatrix}
SΔ=21
x1x2x3y1y2y3111
。
为了表示方便,这里用三角坐标代替原始参数,即
f
(
α
,
β
,
γ
)
=
f
(
α
p
1
+
β
p
2
+
γ
p
3
)
f(\alpha,\beta,\gamma)=f(\alpha p_1 + \beta p_2 + \gamma p_3)
f(α,β,γ)=f(αp1+βp2+γp3),同时约定
α
+
β
+
γ
=
1
α+β+γ=1
α+β+γ=1。
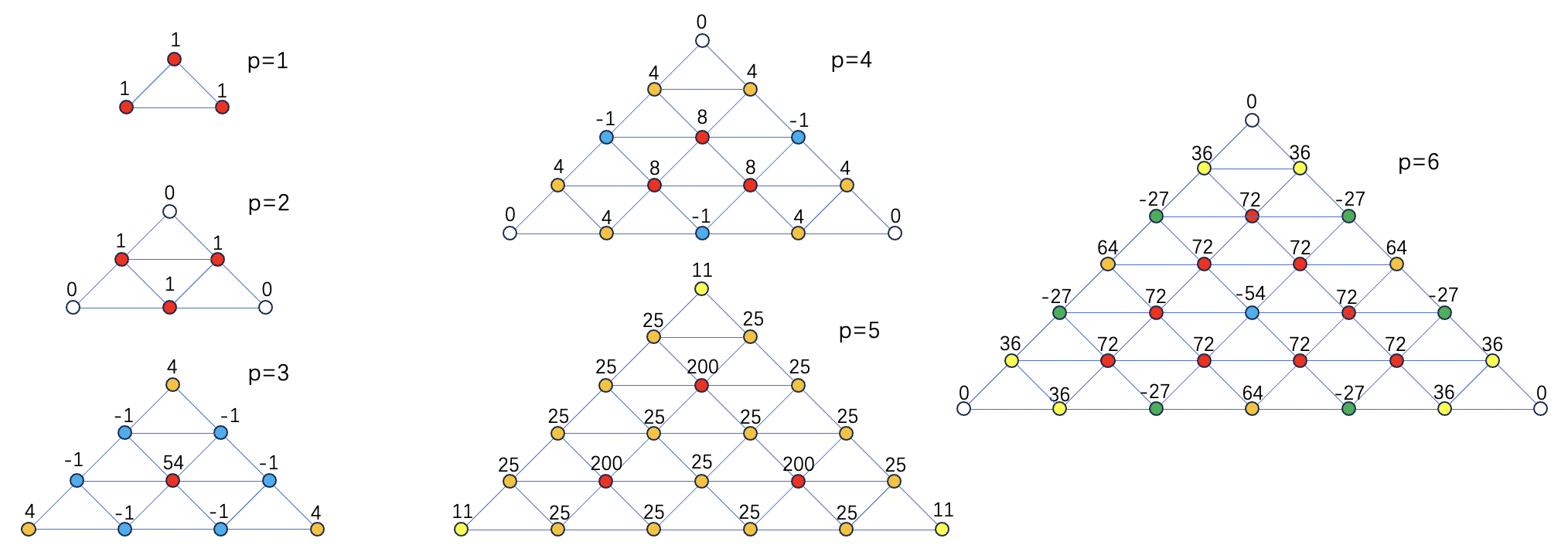
牛顿-柯特斯公式(等距情况)
| n | 精度p | 采样数 | ( α , β , γ ) × n (\alpha,\beta,\gamma)\times n (α,β,γ)×n | A A A |
|---|---|---|---|---|
| 1 | 1 | 3 | 0 , 0 , 2 0,0,2 0,0,2 | 1 / 3 1/3 1/3 |
| 2 | 2 | 3 | 1 , 1 , 0 1,1,0 1,1,0 | 1 / 3 1/3 1/3 |
| 3 | 3 | 10 | 0 , 0 , 3 0 , 1 , 2 1 , 1 , 1 0,0,3\\0,1,2\\1,1,1 0,0,30,1,21,1,1 | 4 / 120 9 / 120 54 / 120 4/120\\9/120\\54/120 4/1209/12054/120 |
| 4 | 4 | 12 | 0 , 1 , 3 0 , 2 , 2 1 , 1 , 2 0,1,3\\0,2,2\\1,1,2 0,1,30,2,21,1,2 | 4 / 45 − 1 / 45 8 / 45 4/45\\-1/45\\8/45 4/45−1/458/45 |
| 5 | 5 | 21 | 0 , 0 , 5 0 , 1 , 4 0 , 2 , 3 1 , 1 , 3 1 , 2 , 2 0,0,5\\0,1,4\\0,2,3\\1,1,3\\1,2,2 0,0,50,1,40,2,31,1,31,2,2 | 11 / 1008 25 / 1008 25 / 1008 200 / 1008 25 / 1008 11/1008\\25/1008\\25/1008\\200/1008\\25/1008 11/100825/100825/1008200/100825/1008 |
| 6 | 6 | 25 | 0 , 1 , 5 0 , 2 , 4 0 , 3 , 3 1 , 1 , 4 1 , 2 , 3 2 , 2 , 2 0,1,5\\0,2,4\\0,3,3\\1,1,4\\1,2,3\\2,2,2 0,1,50,2,40,3,31,1,41,2,32,2,2 | 36 / 840 − 27 / 840 64 / 840 72 / 840 72 / 840 − 54 / 840 36/840\\-27/840\\64/840\\72/840\\72/840\\-54/840 36/840−27/84064/84072/84072/840−54/840 |
高斯积分(不等距情况)
这里主要说明Dunavant Rule.
例如要求3次精度时,可以用以下式子表示
∬
Δ
f
(
x
,
y
)
d
S
≈
S
Δ
[
−
9
16
f
(
s
3
)
+
25
48
(
f
(
2
p
1
+
s
5
)
+
f
(
2
p
2
+
s
5
)
+
f
(
2
p
3
+
s
5
)
)
]
\iint_\Delta f(x,y)dS\approx S_\Delta [\frac{-9}{16}f(\frac{s}{3})+\frac{25}{48}(f(\frac{2p_1+s}{5})+f(\frac{2p_2+s}{5})+f(\frac{2p_3+s}{5}))]
∬Δf(x,y)dS≈SΔ[16−9f(3s)+4825(f(52p1+s)+f(52p2+s)+f(52p3+s))]
其中
s
=
p
1
+
p
2
+
p
3
s=p_1+p_2+p_3
s=p1+p2+p3
更多数值如下:
| 精度p | 采样数 | ( α , β , γ ) (\alpha,\beta,\gamma) (α,β,γ) | A A A |
|---|---|---|---|
| 1 | 1 | 1 / 3 , 1 / 3 , 1 / 3 1/3,1/3,1/3 1/3,1/3,1/3 | 1 |
| 2 | 3 | 1 / 6 , 1 / 6 , 2 / 3 1/6,1/6,2/3 1/6,1/6,2/3 | 1 / 3 1/3 1/3 |
| 3 | 4 | 1 / 3 , 1 / 3 , 1 / 3 1 / 5 , 1 / 5 , 3 / 5 1/3,1/3,1/3\\1/5,1/5,3/5 1/3,1/3,1/31/5,1/5,3/5 | − 9 / 16 = − 0.5625 25 / 48 = 0.52083333 -9/16=-0.5625\\25/48=0.52083333 −9/16=−0.562525/48=0.52083333 |
| 4 | 6 | 0.445948490 9 [ a ] , 0.4459484909 , 0.1081030182 0.091576213 5 [ b ] , 0.0915762135 , 0.8168475730 0.445 948 490 9_{[a]},0.445 948 490 9,0.108 103 018 2\\0.091 576 213 5_{[b]},0.091 576 213 5,0.816 847 573 0 0.4459484909[a],0.4459484909,0.10810301820.0915762135[b],0.0915762135,0.8168475730 | 0.223381589 7 [ c ] 0.109951743 7 [ d ] 0.223 381 589 7_{[c]}\\0.109 951 743 7_{[d]} 0.2233815897[c]0.1099517437[d] |
| 5 | 7 | 1 / 3 , 1 / 3 , 1 / 3 0.470142064 1 [ a ] , 0.4701420641 , 0.0597158718 0.101286507 3 [ b ] , 0.1012865073 , 0.7974269854 1/3,1/3,1/3\\0.470 142 064 1_{[a]},0.470 142 064 1,0.059 715 871 8\\0.101 286 507 3_{[b]},0.101 286 507 3,0.797 426 985 4 1/3,1/3,1/30.4701420641[a],0.4701420641,0.05971587180.1012865073[b],0.1012865073,0.7974269854 | 9 / 40 = 0.225 0.132394152 8 [ c ] 0.125939180 5 [ d ] 9/40=0.225\\0.132 394 152 8_{[c]}\\0.125 939 180 5_{[d]} 9/40=0.2250.1323941528[c]0.1259391805[d] |
| 6 | 12 | 0.2492867452 , 0.2492867452 , 0.5014265096 0.0630890145 , 0.0630890145 , 0.8738219710 0.0531450498 , 0.3103524510 , 0.6365024991 0.249 286 745 2,0.249 286 745 2,0.501 426 509 6\\0.063 089 014 5,0.063 089 014 5,0.873 821 971 0\\0.053 145 049 8,0.310 352 451 0,0.636 502 499 1 0.2492867452,0.2492867452,0.50142650960.0630890145,0.0630890145,0.87382197100.0531450498,0.3103524510,0.6365024991 | 0.1167862757 0.0508449064 0.0828510756 0.116 786 275 7\\0.050 844 906 4\\0.082 851 075 6 0.11678627570.05084490640.0828510756 |
备注:
- 因对称性关系, α , β , γ \alpha,\beta,\gamma α,β,γ 可以两两互换,上面表格只记录其中一组数据
- 精度4: a , b = 40 − 5 10 ± 950 − 220 10 90 a,b=\frac{40-5\sqrt{10}\pm\sqrt{950 - 220\sqrt{10}}}{90} a,b=9040−510±950−22010为 135 x 4 − 240 x 3 + 120 x 2 − 20 x + 1 = 0 135x^4 - 240x^3 + 120x^2 - 20x+ 1=0 135x4−240x3+120x2−20x+1=0 的解, c = ( 2 b − 1 ) ( 6 b − 1 ) 12 ( b − a ) ( 3 a + 3 b − 2 ) , d = ( 2 a − 1 ) ( 6 a − 1 ) 12 ( a − b ) ( 3 a + 3 b − 2 ) c=\frac{(2b - 1)(6b - 1)}{12(b-a)(3a + 3b - 2)},d=\frac{(2a - 1)(6a - 1)}{12(a - b)(3a + 3b - 2)} c=12(b−a)(3a+3b−2)(2b−1)(6b−1),d=12(a−b)(3a+3b−2)(2a−1)(6a−1)
- 精度5:
a
,
b
=
(
6
±
15
)
/
21
,
c
,
d
=
(
155
±
15
)
/
1200
a,b=(6 \pm \sqrt{15}) / 21,\ c,d=(155 \pm \sqrt{15})/1200
a,b=(6±15)/21, c,d=(155±15)/1200

更多信息可以参考论文
High Degree Efficient Symmetrical Gaussian Quadrature Rules For The Triangle - Dunavant
Symmetric quadrature rules on a triangle
三重积分-四面体区域
∭
T
f
(
x
,
y
,
z
)
d
V
≈
V
T
∑
k
=
1
N
A
k
f
(
α
k
,
β
k
,
γ
k
,
δ
k
)
\iiint_T f(x,y,z)dV\approx V_T \sum_{k=1}^N A_kf(\alpha_k,\beta_k,\gamma_k,\delta_k)
∭Tf(x,y,z)dV≈VTk=1∑NAkf(αk,βk,γk,δk)
其中积分区域为四面体T ,其顶点为
p
i
=
(
x
i
,
y
i
,
z
i
)
,
i
=
1
,
2
,
3
,
4
p_i=(x_i,y_i,z_i), i=1,2,3,4
pi=(xi,yi,zi),i=1,2,3,4,并且其体积记为
V
T
V_T
VT,且有
V
T
=
1
6
∣
x
1
y
1
z
1
1
x
2
y
2
z
2
1
x
3
y
3
z
3
1
x
4
y
4
z
4
1
∣
V_T=\frac{1}{6}\begin{vmatrix}x_1&y_1&z_1&1\\x_2&y_2&z_2&1\\x_3&y_3&z_3&1\\x_4&y_4&z_4&1\end{vmatrix}
VT=61
x1x2x3x4y1y2y3y4z1z2z3z41111
。
为了表示方便,这里用三角坐标代替原始参数,即
f
(
α
,
β
,
γ
,
δ
)
=
f
(
α
p
1
+
β
p
2
+
γ
p
3
+
δ
p
4
)
f(\alpha,\beta,\gamma,\delta)=f(\alpha p_1 + \beta p_2 + \gamma p_3+\delta p_4)
f(α,β,γ,δ)=f(αp1+βp2+γp3+δp4),同时约定
α
+
β
+
γ
+
δ
=
1
α+β+γ+δ=1
α+β+γ+δ=1,且
α
,
β
,
γ
,
δ
∈
[
0
,
1
]
α,β,γ,δ \in[0,1]
α,β,γ,δ∈[0,1]。
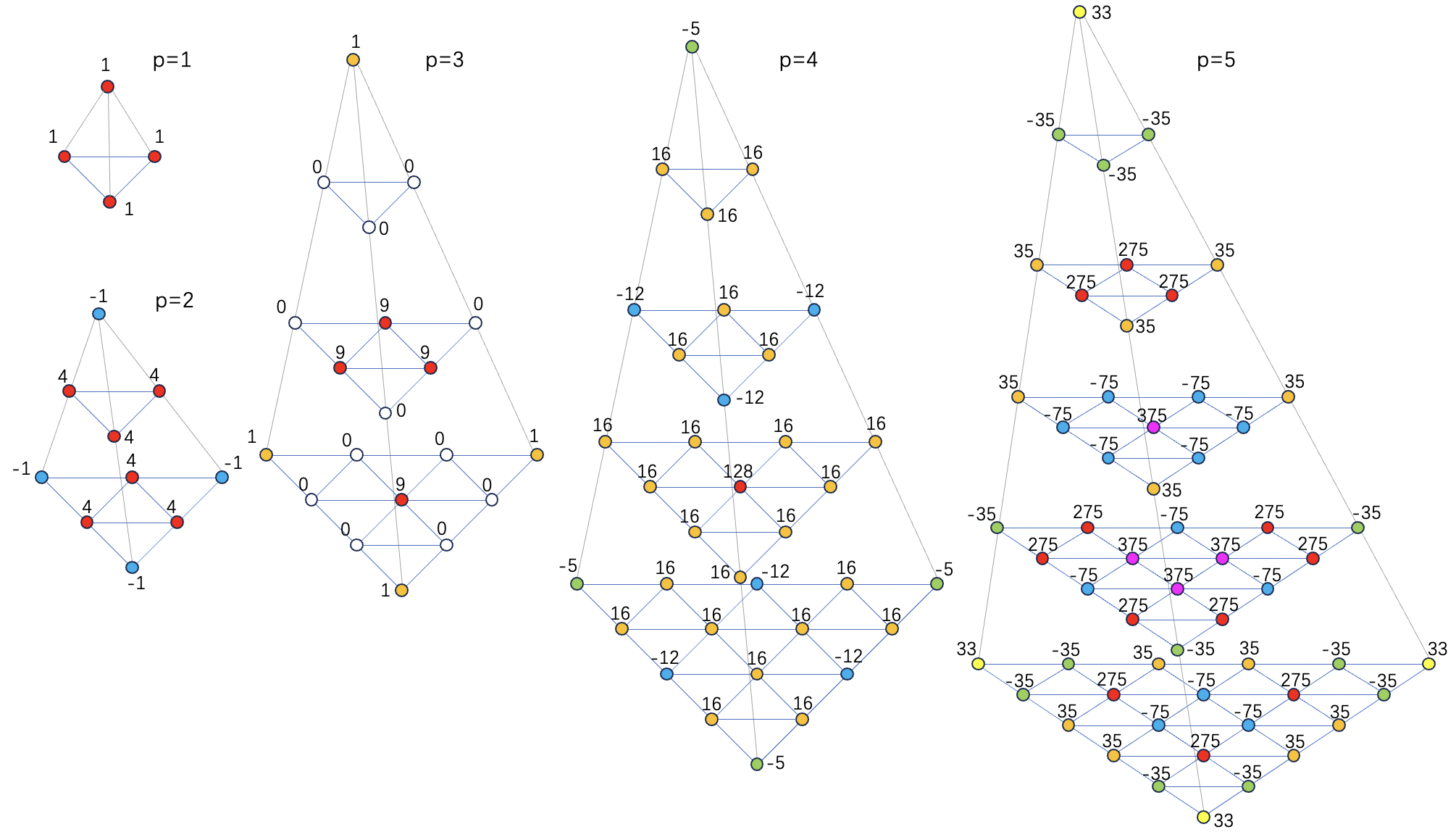
牛顿-柯特斯公式(等距情况)
| n | 精度p | 采样数 | ( α , β , γ , δ ) × n (\alpha,\beta,\gamma,\delta)\times n (α,β,γ,δ)×n | A A A |
|---|---|---|---|---|
| 1 | 1 | 4 | 1 , 1 , 1 , 1 1,1,1,1 1,1,1,1 | 1 / 4 1/4 1/4 |
| 2 | 2 | 10 | 0 , 0 , 0 , 2 0 , 0 , 1 , 1 0,0,0,2\\0,0,1,1 0,0,0,20,0,1,1 | − 1 / 20 4 / 20 -1/20\\4/20 −1/204/20 |
| 3 | 3 | 8 | 0 , 0 , 0 , 3 0 , 1 , 1 , 1 0,0,0,3\\0,1,1,1 0,0,0,30,1,1,1 | 1 / 40 9 / 40 1/40\\9/40 1/409/40 |
| 4 | 4 | 35 | 0 , 0 , 0 , 4 0 , 0 , 1 , 3 0 , 0 , 2 , 2 0 , 1 , 1 , 2 1 , 1 , 1 , 1 0,0,0,4\\0,0,1,3\\0,0,2,2\\0,1,1,2\\1,1,1,1 0,0,0,40,0,1,30,0,2,20,1,1,21,1,1,1 | − 5 / 420 16 / 420 − 12 / 420 16 / 420 128 / 420 -5/420\\16/420\\-12/420\\16/420\\128/420 −5/42016/420−12/42016/420128/420 |
| 5 | 5 | 56 | 0 , 0 , 0 , 5 0 , 0 , 1 , 4 0 , 0 , 2 , 3 0 , 1 , 1 , 3 0 , 1 , 2 , 2 1 , 1 , 1 , 2 0,0,0,5\\0,0,1,4\\0,0,2,3\\0,1,1,3\\0,1,2,2\\1,1,1,2 0,0,0,50,0,1,40,0,2,30,1,1,30,1,2,21,1,1,2 | 33 / 4032 − 35 / 4032 35 / 4032 275 / 4032 − 75 / 4032 375 / 4032 33/4032\\-35/4032\\35/4032\\275/4032\\-75/4032\\375/4032 33/4032−35/403235/4032275/4032−75/4032375/4032 |
高斯积分(不等距情况)
这里主要说明Keast Rule.
例如要求3次精度时,可以用以下式子表示
∭
T
f
(
x
,
y
,
z
)
d
V
≈
V
T
[
−
4
5
f
(
s
4
)
+
9
20
(
f
(
2
p
1
+
s
6
)
+
f
(
2
p
2
+
s
6
)
+
f
(
2
p
3
+
s
6
)
+
f
(
2
p
4
+
s
6
)
)
]
\iiint_T f(x,y,z)dV\approx V_T [\frac{-4}{5}f(\frac{s}{4})+\frac{9}{20}(f(\frac{2p_1+s}{6})+f(\frac{2p_2+s}{6})+f(\frac{2p_3+s}{6})+f(\frac{2p_4+s}{6}))]
∭Tf(x,y,z)dV≈VT[5−4f(4s)+209(f(62p1+s)+f(62p2+s)+f(62p3+s)+f(62p4+s))]
其中
s
=
p
1
+
p
2
+
p
3
+
p
4
s=p_1+p_2+p_3+p_4
s=p1+p2+p3+p4
更多数值如下:
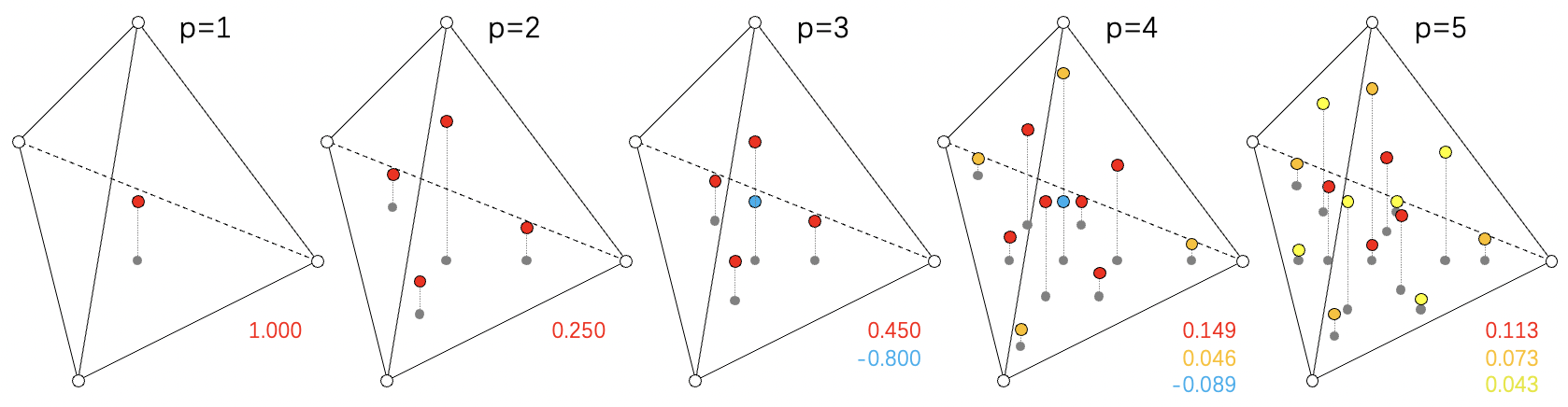
| 精度p | 采样数 | ( α , β , γ , δ ) (\alpha,\beta,\gamma,\delta) (α,β,γ,δ) | A A A |
|---|---|---|---|
| 1 | 1 | 1 / 4 [ × 4 ] 1/4 [\times 4] 1/4[×4] | 1 |
| 2 | 4 | 0.138196601 1 [ a ] [ × 3 ] , 0.5854101966 0.138 196 601 1_{[a]}[\times 3],0.585 410 196 6 0.1381966011[a][×3],0.5854101966 | 1 / 4 = 0.25 1/4=0.25 1/4=0.25 |
| 3 | 5 | 1 / 4 [ × 4 ] 1 / 6 [ × 3 ] , 1 / 2 1/4 [\times 4]\\1/6 [\times 3],1/2 1/4[×4]1/6[×3],1/2 | − 4 / 5 = − 0.8 9 / 20 = 0.45 -4/5=-0.8\\9/20=0.45 −4/5=−0.89/20=0.45 |
| 4 | 11 | 1 / 4 [ × 4 ] 1 / 14 = 0.0714285714 [ × 3 ] , 11 / 14 = 0.7857142857 0.399403576 2 [ a ] [ × 2 ] , 0.1005964238 [ × 2 ] 1/4 [\times 4]\\1/14=0.071 428 571 4[\times 3],11/14=0.785 714 285 7\\0.399 403 576 2_{[a]}[\times 2],0.100 596 423 8[\times 2] 1/4[×4]1/14=0.0714285714[×3],11/14=0.78571428570.3994035762[a][×2],0.1005964238[×2] | − 148 / 1875 = − 0.0789333 343 / 7500 = 0.0457333 56 / 375 = 0.1493333 -148/1875=-0.0789333\\343/7500=0.0457333\\56/375=0.1493333 −148/1875=−0.0789333343/7500=0.045733356/375=0.1493333 |
| 5 | 14 | 0.092735250 3 [ a ] [ × 3 ] , 0.7217942491 0.310885919 3 [ b ] [ × 3 ] , 0.0673422422 0.454496295 9 [ c ] [ × 2 ] , 0.0455037041 [ × 2 ] 0.092 735 250 3_{[a]}[\times 3],0.721 794 249 1\\0.310 885 919 3_{[b]}[\times 3],0.067 342 242 2\\0.454 496 295 9_{[c]}[\times 2],0.045 503 704 1[\times 2] 0.0927352503[a][×3],0.72179424910.3108859193[b][×3],0.06734224220.4544962959[c][×2],0.0455037041[×2] | 0.073493043 1 [ d ] 0.112687925 7 [ e ] 0.042546020 8 [ f ] 0.073 493 043 1_{[d]}\\0.112 687 925 7_{[e]}\\0.042 546 020 8_{[f]} 0.0734930431[d]0.1126879257[e]0.0425460208[f] |
备注:
- 因对称性关系, α , β , γ , δ \alpha,\beta,\gamma,\delta α,β,γ,δ 可以两两互换,上面表格只记录其中一组数据。另外,重复的数字不再单独写出,直接用 [ × N ] [\times N] [×N] 表示出现了N次。
- 精度1-4:存在于Keast Unit Tet Rule
- 精度2: a = ( 5 − 5 ) / 20 a=(5 - \sqrt{5})/20 a=(5−5)/20
- 精度4: a = ( 14 + 70 ) / 56 a=(14+\sqrt{70})/56 a=(14+70)/56
- 精度5: x = 0.6690997604212774 x=0.6690997604212774 x=0.6690997604212774为 133 x 3 − 175 x 2 + 71 x − 9 = 0 133x^3 - 175x^2 + 71x - 9=0 133x3−175x2+71x−9=0的一个解(其他解会引起负数或复数), a , b = 21 x − 7 ± 105 x 2 − 62 x + 9 112 x − 40 , c = 1 + x 4 , d = ( 42 x − 8 ) b − 7 x + 2 840 x ( b − a ) ( 4 a − 1 ) 2 , e = ( 42 x − 8 ) a − 7 x + 2 840 x ( a − b ) ( 4 b − 1 ) 2 , f = 2 105 x 2 a,b=\frac{21x-7\pm \sqrt{105x^2 - 62x + 9}}{112x-40},c=\frac{1+\sqrt{x}}{4}, d= \frac{(42x - 8)b - 7x + 2}{840x(b-a)(4a - 1)^2},e= \frac{(42x - 8)a- 7x + 2}{840x(a - b)(4b - 1)^2},f=\frac{2}{105x^2} a,b=112x−4021x−7±105x2−62x+9,c=41+x,d=840x(b−a)(4a−1)2(42x−8)b−7x+2,e=840x(a−b)(4b−1)2(42x−8)a−7x+2,f=105x22
具体可以参考文章:
Keast Unit Tet Rule
Moderate Degree Tetrahedral Quadrature Formulas
Numerical Integration
Integration methods
Exact Integrations of Polynomials and Symmetric Quadrature Formulas over Arbitrary Polyhedral Grids
A SET OF SYMMETRIC QUADRATURE RULES ON TRIANGLES AND TETRAHEDRA
结尾
因篇幅问题,数值积分还有许多课题没有写上,例如圆形、球体等曲面图形的多重积分,这部分将在下一篇补上,有兴趣的读者可以关注。





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








