椭圆曲线定义
数学上,椭圆曲线并不是椭圆
x
2
/
a
2
+
y
2
/
b
2
=
1
x^2/a^2+y^2/b^2=1
x2/a2+y2/b2=1,而是
y
2
=
x
3
+
a
x
+
b
y^2=x^3+ax+b
y2=x3+ax+b 这样形式的方程。
椭圆曲线来源于计算椭圆弧长的椭圆积分
∫
d
x
x
4
+
a
x
3
+
b
x
2
+
c
x
+
d
\int\frac{dx}{\sqrt{x^4+ax^3+bx^2+cx+d}}
∫x4+ax3+bx2+cx+ddx,从而注意到方程
y
2
=
x
4
+
a
x
3
+
b
x
2
+
c
x
+
d
y^2=x^4+ax^3+bx^2+cx+d
y2=x4+ax3+bx2+cx+d,而这个方程可以转换成
y
2
=
x
3
+
a
x
+
b
y^2=x^3+ax+b
y2=x3+ax+b的形式。
另外,椭圆曲线定义是域上亏格为1的光滑射影曲线(这个内容水很深,留到新文章讨论)。
椭圆曲线基本型式
| 型式 | 椭圆曲线 | 备注 |
|---|---|---|
| a-form | y 2 + a 1 x y + a 3 y = x 3 + a 2 x 2 + a 4 x + a 6 y^2+a_1xy+a_3y=x^3+a_2x^2+a_4x+a_6 y2+a1xy+a3y=x3+a2x2+a4x+a6 | 令 y = η − ( a 1 x + a 3 ) / 2 y=\eta-(a_1x+a_3)/2 y=η−(a1x+a3)/2, 可得到b-form |
| b-form | η 2 = x 3 + b 2 x 2 + b 4 x + b 6 \eta^2=x^3+b_2x^2+b_4x+b_6 η2=x3+b2x2+b4x+b6 | 令 x = ξ − b 2 / 3 x=\xi-b_2/3 x=ξ−b2/3,可得到c-form |
| c-form | η 2 = ξ 3 + c 4 ξ + c 6 \eta^2=\xi^3+c_4\xi+c_6 η2=ξ3+c4ξ+c6 |
其中,
{
b
2
=
a
2
+
a
1
2
/
4
b
4
=
a
4
+
a
1
a
3
/
2
b
6
=
a
6
+
a
3
2
/
4
\begin{cases} b_2=a_2+a_1^2/4 \\ b_4=a_4+a_1a_3/2 \\ b_6=a_6+a_3^2/4 \end{cases}
⎩
⎨
⎧b2=a2+a12/4b4=a4+a1a3/2b6=a6+a32/4 ,以及
{
c
4
=
−
b
2
2
/
3
+
b
4
c
6
=
2
b
2
3
/
27
−
b
2
b
4
/
3
+
b
6
\begin{cases} c_4=- b_2^2/3 + b_4\\ c_6=2b_2^3/27 - b_2b_4/3 + b_6 \end{cases}
{c4=−b22/3+b4c6=2b23/27−b2b4/3+b6
判别式:
Δ
=
−
16
(
4
c
4
3
+
27
c
6
2
)
\Delta=-16(4c_4^3+27c_6^2)
Δ=−16(4c43+27c62),仅当
Δ
≠
0
\Delta \ne 0
Δ=0时为椭圆曲线方程
椭圆曲线转换
接下来,将介绍如何将各类三次方程转换成椭圆曲线。
将一般三次曲线转化成椭圆曲线
笔者在参考资料 Matsuura-projective_transformation.pdf 上,增加对最后的
P
(
x
)
y
2
+
Q
(
x
)
y
+
R
(
x
)
=
0
P(x)y^2+Q(x)y+R(x)=0
P(x)y2+Q(x)y+R(x)=0 转换过程。
具体算法如下
对于一般的三次曲线
E
:
F
(
x
,
y
,
z
)
=
a
0
x
3
+
a
1
x
2
y
+
a
2
x
y
2
+
a
3
y
3
+
b
0
x
2
+
b
1
x
y
+
b
2
y
2
+
c
1
x
+
c
2
y
+
d
=
0
E:F(x,y,z)=a_0x^3+a_1x^2y+a_2xy^2+a_3y^3+b_0x^2+b_1xy+b_2y^2+c_1x+c_2y+d=0
E:F(x,y,z)=a0x3+a1x2y+a2xy2+a3y3+b0x2+b1xy+b2y2+c1x+c2y+d=0
这里以
F
1
(
x
,
y
,
z
)
=
2
x
3
+
3
y
3
−
5
=
0
F_1(x,y,z)=2x^3+3y^3-5=0
F1(x,y,z)=2x3+3y3−5=0为例进行说明
| 步骤 | 说明 | 示例 |
|---|---|---|
| 1 | 齐次化,将 x , y x,y x,y 分别替换成 x / z , y / z x/z,y/z x/z,y/z, 再乘上 z 3 z^3 z3 | 重写 F 1 F_1 F1为 F 1 ( x , y , z ) = 2 x 3 + 3 y 3 − 5 z 3 = 0 F_1(x,y,z)=2x^3+3y^3-5z^3=0 F1(x,y,z)=2x3+3y3−5z3=0 |
| 2 | 找到一个非全零的解 ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) (x0,y0,z0),使得 F ( x 0 , y 0 , z 0 ) = 0 F(x_0,y_0,z_0)=0 F(x0,y0,z0)=0 | 找到 ( 1 , 1 , 1 ) (1,1,1) (1,1,1) 为 F 1 ( x , y , z ) = 0 F_1(x,y,z)=0 F1(x,y,z)=0的解 |
| 3 | 计算 F ( x , y , z ) F(x,y,z) F(x,y,z) 在 ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) (x0,y0,z0) 上的切平面,即 W ( x , y , z ) = ( x − x 0 ) F x ′ ( x 0 ) + ( y − y 0 ) F y ′ ( y 0 ) + ( z − z 0 ) F z ′ ( z 0 ) = 0 W(x,y,z)=(x-x_0)F'_x(x_0)+(y-y_0)F'_y(y_0)+(z-z_0)F'_z(z_0)=0 W(x,y,z)=(x−x0)Fx′(x0)+(y−y0)Fy′(y0)+(z−z0)Fz′(z0)=0 | F 1 ( x , y , z ) F_1(x,y,z) F1(x,y,z)在 ( 1 , 1 , 1 ) (1,1,1) (1,1,1)上的切平面为 W = 2 x + 3 y − 5 z = 0 W=2x + 3y - 5z=0 W=2x+3y−5z=0 |
| 4 | 计算 W ( x , y , z ) = 0 W(x,y,z)=0 W(x,y,z)=0与 F ( x , y , z ) = 0 F(x,y,z)=0 F(x,y,z)=0的交点 ( x 1 , y 1 , z 1 ) (x_1,y_1,z_1) (x1,y1,z1) | 由 W = 0 W=0 W=0 得到 z = ( 2 x + 3 y ) / 5 z=(2x+3y)/5 z=(2x+3y)/5 得到 0 = F ( x , y , ( 2 x + 3 y ) / 5 ) = 6 ( x − y ) 2 ( 7 x + 8 y ) / 25 0=F(x,y,(2x+3y)/5)=6(x - y)^2(7x + 8y)/25 0=F(x,y,(2x+3y)/5)=6(x−y)2(7x+8y)/25,即 ( x 1 , y 1 , z 1 ) = λ ( − 8 , 7 , 1 ) (x_1,y_1,z_1)=\lambda(-8,7,1) (x1,y1,z1)=λ(−8,7,1) |
| 5 | 计算 F ( x , y , z ) F(x,y,z) F(x,y,z) 在 ( x 1 , y 1 , z 1 ) (x_1,y_1,z_1) (x1,y1,z1) 上的切平面 U ( x , y , z ) U(x,y,z) U(x,y,z) | F 1 ( x , y , z ) F_1(x,y,z) F1(x,y,z)在 ( − 8 , 7 , 1 ) (-8,7,1) (−8,7,1)上的切平面为 U = 128 x + 147 y − 5 z = 0 U=128x + 147y - 5z=0 U=128x+147y−5z=0 |
| 6 | 找一个与 U = 0 , W = 0 U=0,W=0 U=0,W=0无关的线性方程 V ( x , y , z ) V(x,y,z) V(x,y,z),使得 V ( x 0 , y 0 , z 0 ) = 0 V(x_0,y_0,z_0)=0 V(x0,y0,z0)=0 | 因为有 x 0 + y 0 − 2 z 0 = 0 x_0+y_0-2z_0=0 x0+y0−2z0=0, 所以设 V = x + y − 2 z V=x+y-2z V=x+y−2z |
| 7 | 根据 ( U , V , W ) T = M × ( x , y , z ) T (U,V,W)^T=M\times (x,y,z)^T (U,V,W)T=M×(x,y,z)T, 解出 ( x , y , z ) T = M − 1 ( U , V , W ) T (x,y,z)^T=M^{-1}(U,V,W)^T (x,y,z)T=M−1(U,V,W)T | 由 ( U V W ) = ( 128 147 − 5 1 1 − 2 2 3 − 5 ) ( x y z ) \begin{pmatrix}U \\ V \\ W\end{pmatrix}=\begin{pmatrix}128&147&-5 \\ 1&1&-2 \\ 2&3&-5\end{pmatrix}\begin{pmatrix} x \\ y \\ z\end{pmatrix} UVW = 1281214713−5−2−5 xyz ,得到 ( x y z ) = 1 270 ( 1 720 − 289 1 − 630 251 1 − 90 − 19 ) ( U V W ) \\\begin{pmatrix}x \\ y \\ z\end{pmatrix}=\frac{1}{270}\begin{pmatrix}1&720&-289 \\1&-630&251\\1&-90&-19\end{pmatrix}\begin{pmatrix}U \\ V \\ W\end{pmatrix} xyz =2701 111720−630−90−289251−19 UVW |
| 8 | 将 ( U , V , W ) (U,V,W) (U,V,W)为参数的 ( x , y , z ) (x,y,z) (x,y,z)代入 F ( x , y , z ) = 0 F(x,y,z)=0 F(x,y,z)=0,再令W=1并化简 | F 1 = 810 ( U 2 W + 8100 U V 2 − 6660 U V W + 1312 U W 2 + 5040 V W 2 − 989 W 3 ) = 0 F_1=810(U^2W + 8100UV^2 - 6660UVW + 1312UW^2 + 5040VW^2 - 989W^3)=0 F1=810(U2W+8100UV2−6660UVW+1312UW2+5040VW2−989W3)=0, 即 F 2 = ( 8100 U ) V 2 + ( − 6660 U + 5040 ) V + ( U 2 + 1312 U − 989 ) = 0 F_2=(8100U)V^2 +(-6660U+ 5040)V+(U^2+1312U- 989)=0 F2=(8100U)V2+(−6660U+5040)V+(U2+1312U−989)=0 |
| 9 | 计算 F 2 F_2 F2的判别式,令其为 Q 2 Q^2 Q2 | Q 2 = ( − 6660 U + 5040 ) 2 − 4 ( 8100 U ) ( U 2 + 1312 U − 989 ) = − 32400 U 3 + 1846800 U 2 − 35089200 U + 25401600 Q^2=(-6660U+ 5040)^2-4(8100U)(U^2+1312U- 989)=-32400 U^3 + 1846800 U^2 - 35089200 U + 25401600 Q2=(−6660U+5040)2−4(8100U)(U2+1312U−989)=−32400U3+1846800U2−35089200U+25401600 |
| 10 | 转换为椭圆曲线 | 令 U = 19 − p , Q = 180 q U= 19 - p ,Q= 180q U=19−p,Q=180q, 得到 q 2 = p 3 − 6075 \\q^2=p^3- 6075 q2=p3−6075, 并且有 x = p 2 − 45 p + 270 − 8 q y = p 2 − 30 p + 405 + 7 q z = p 2 + 18 p − 675 + q \\x =p^2-45p+270-8q\\y =p^2 - 30p + 405+7q\\z =p^2 + 18p - 675+q x=p2−45p+270−8qy=p2−30p+405+7qz=p2+18p−675+q |
备注:整个算法最困难的是第2步(找到一个非全零的解),有些椭圆曲线本身就没有有理解。第2步的解只是影响到(x,y,z)与(p,q)的映射关系,无不影响最后转换出来的椭圆曲线。
具体过程可以参考代码:
import sympy
from fractions import Fraction
def Weierstrass(F, x0, y0, z0):
x0 = Fraction(1, 1) * x0
y0 = Fraction(1, 1) * y0
z0 = Fraction(1, 1) * z0
x,y,z = sympy.symbols("x y z")
# 确定 (x0,y0,z0) 是 F=0 上的点
if F.subs({x: x0, y: y0, z: z0}) != 0:
print("error", F, "@", x0, y0, z0)
return
# 计算过点(x0,y0,z0)的切平面zf
zf = sympy.diff(F, x).subs({x:x0, y:y0, z:z0})*(x - x0) + \
sympy.diff(F, y).subs({x:x0, y:y0, z:z0})*(y - y0) + \
sympy.diff(F, z).subs({x:x0, y:y0, z:z0})*(z - z0)
mat = sympy.matrices.zeros(3, 3)
mat[2, 0] = zf.coeff(x)
mat[2, 1] = zf.coeff(y)
mat[2, 2] = zf.coeff(z)
# 计算切平面zf与F0的交点(x1,y1,z1)
if zf.coeff(y) != 0:
yf = y - zf / zf.coeff(y)
f0 = F.subs({y: yf}) / (z0 * x - x0 * z) / (z0 * x - x0 * z)
f0 = sympy.ratsimp(f0)
x1 = -f0.coeff(z)
z1 = f0.coeff(x)
y1 = yf.subs({x: x1, z: z1})
elif zf.coeff(z) != 0:
yf = z - zf / zf.coeff(z)
f0 = F.subs({z: yf}) / (y0 * x - x0 * y) / (y0 * x - x0 * y)
f0 = sympy.ratsimp(f0)
x1 = -f0.coeff(y)
y1 = f0.coeff(x)
z1 = yf.subs({x: x1, y: y1})
else:
print("error2 ", zf)
return
# 计算过点(x1,y1,z1)的切平面xf
xf = sympy.diff(F, x).subs({x:x1, y:y1, z:z1})*(x - x1) + \
sympy.diff(F, y).subs({x:x1, y:y1, z:z1})*(y - y1) + \
sympy.diff(F, z).subs({x:x1, y:y1, z:z1})*(z - z1)
mat[0, 0] = xf.coeff(x)
mat[0, 1] = xf.coeff(y)
mat[0, 2] = xf.coeff(z)
# 随机设置yf
if z0 == 0:
mat[1, 0] = y0
mat[1, 1] = -x0
mat[1, 2] = 0
else:
mat[1, 0] = 1
mat[1, 1] = 1
mat[1, 2] = -(x0+y0)/z0
#print(mat)
# 此时有 (p,t,1) = mat * (x,y,z), 解得 (x,y,z) = inv * (p,t,1)
inv = mat.inv()
#print(inv)
p,q,t = sympy.symbols("p q t")
X = inv[0, 0] * p + inv[0, 1] * t + inv[0, 2]
Y = inv[1, 0] * p + inv[1, 1] * t + inv[1, 2]
Z = inv[2, 0] * p + inv[2, 1] * t + inv[2, 2]
# 将 (x,y,z) 代入 F = 0, 得到 G = q2(p)*t^2 + q1(p)*t + q0(p) = 0的方程
F1 = sympy.expand(F.subs({x:X, y:Y, z:Z}))
#print("0 =", F1)
q2 = F1.coeff(t**2)
q1 = F1.coeff(t)
q0 = F1 - q2 * t**2 - q1 * t
# 求G的二次方程特征值,得到最终的方程 q^2=H(p)
F2 = sympy.expand(q1 * q1 - 4 * q2 * q0)
print("solve q**2 =", F2)
t = (-q1 + q) / (2 * q2)
# 以(p,q)为参数, 重新计算(x,y,z)
xf = inv[0, 0] * p + inv[0, 1] * t + inv[0, 2]
yf = inv[1, 0] * p + inv[1, 1] * t + inv[1, 2]
zf = inv[2, 0] * p + inv[2, 1] * t + inv[2, 2]
print("x =", sympy.factor(xf))
print("y =", sympy.factor(yf))
print("z =", sympy.factor(zf))
print("check ", sympy.factor(F.subs({x:xf, y:yf, z:zf})))
x,y,z = sympy.symbols("x y z")
F = 1*x**3 + 2*y**3 + 3*z**3 + 4*x*y*z
Weierstrass(F, -1, 1, 1)
将四次曲线 y 2 = q 2 x 2 + a x + b + c y^2=q^2x^2+ax+b+c y2=q2x2+ax+b+c 转化成椭圆曲线
y
2
=
q
2
x
4
+
a
x
2
+
b
x
+
c
→
y
=
q
x
2
+
u
(
q
x
2
+
u
)
2
=
q
2
x
4
+
a
x
2
+
b
x
+
c
→
展开化简
(
a
−
2
q
u
)
x
2
+
b
x
+
(
c
−
u
2
)
=
0
→
判别式为
v
2
Δ
=
b
2
−
4
(
a
−
2
q
u
)
(
c
−
u
2
)
=
v
2
→
展开
v
2
=
−
8
q
u
3
+
4
a
u
2
+
8
c
q
u
+
(
b
2
−
4
a
c
)
→
同乘上
q
2
(
q
v
)
2
=
(
−
2
q
u
)
3
+
a
(
−
2
q
u
)
2
−
4
c
q
2
(
−
2
q
u
)
+
(
b
2
−
4
a
c
)
q
2
y^2=q^2x^4+ax^2+bx+c\\ \xrightarrow{y=qx^2+u}(qx^2+u)^2=q^2x^4+ax^2+bx+c\\ \xrightarrow{展开化简}(a-2qu)x^2+bx+(c-u^2)=0\\ \xrightarrow{判别式为v^2}\Delta=b^2-4(a-2qu)(c-u^2)=v^2\\ \xrightarrow{展开} v^2=-8qu^3+4au^2+8cqu+(b^2-4ac)\\ \xrightarrow{同乘上q^2} (qv)^2=(-2qu)^3+a(-2qu)^2-4cq^2(-2qu)+(b^2-4ac)q^2
y2=q2x4+ax2+bx+cy=qx2+u(qx2+u)2=q2x4+ax2+bx+c展开化简(a−2qu)x2+bx+(c−u2)=0判别式为v2Δ=b2−4(a−2qu)(c−u2)=v2展开v2=−8qu3+4au2+8cqu+(b2−4ac)同乘上q2(qv)2=(−2qu)3+a(−2qu)2−4cq2(−2qu)+(b2−4ac)q2
即为椭圆曲线
t
2
=
s
3
+
a
s
2
−
4
c
q
2
s
+
(
b
2
−
4
a
c
)
q
2
t^2=s^3+as^2-4cq^2s+(b^2-4ac)q^2
t2=s3+as2−4cq2s+(b2−4ac)q2
此时
x
=
−
b
q
±
t
2
q
(
a
+
s
)
,
y
=
±
q
(
x
2
−
s
2
)
x=\frac{-bq\pm t}{2q(a+s)},y=\pm q(x^2-\frac{s}{2})
x=2q(a+s)−bq±t,y=±q(x2−2s)
y
2
=
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
q
2
→
令
x
=
1
/
z
,
并同乘
z
4
(
y
z
2
)
2
=
a
+
b
z
+
c
z
2
+
d
z
3
+
q
2
z
4
→
w
=
z
+
d
/
4
q
2
y
′
2
=
q
2
w
4
+
c
′
w
2
+
b
′
w
+
w
y^2=ax^4+bx^3+cx^2+dx+q^2\\ \xrightarrow{令x=1/z,并同乘z^4}(yz^2)^2=a+bz+cz^2+dz^3+q^2z^4\\ \xrightarrow{w=z+d/4q^2}y'^2=q^2w^4+c'w^2+b'w+w
y2=ax4+bx3+cx2+dx+q2令x=1/z,并同乘z4(yz2)2=a+bz+cz2+dz3+q2z4w=z+d/4q2y′2=q2w4+c′w2+b′w+w
再根据上面算法可转化成椭圆曲线
常见方程及转换结果
| 序号 | 方程 | 椭圆曲线方程 | 映射 | 特殊点 |
|---|---|---|---|---|
| 1 | x 3 + y 3 = n x^3+y^3=n x3+y3=n | q 2 = p 3 − 432 n 2 q^2=p^3-432n^2 q2=p3−432n2 | x , y = ( 36 n ± q ) / 6 p x,y=(36n\pm q)/6p x,y=(36n±q)/6p | |
| 2 | x 2 + y 2 = z 2 n = x y / 2 x^2+y^2=z^2\\n=xy/2 x2+y2=z2n=xy/2 | q 2 = p 3 − n 2 p q^2=p^3-n^2p q2=p3−n2p | x = q / p y = 2 n p / q x=q/p\\y=2np/q x=q/py=2np/q | p = ± n , 0 q = 0 p=\pm n,0\\q=0 p=±n,0q=0 |
| 3 | x 3 + y 3 + z 3 = n x y z x^3+y^3+z^3=nxyz x3+y3+z3=nxyz | q 2 = p 3 + n 2 p 2 − 72 n p − 64 n 3 − 432 q^2=p^3+n^2p^2-72np-64n^3-432 q2=p3+n2p2−72np−64n3−432 | x = 6 p + 8 n 2 y , z = − n p − 36 ± q x=6p+8n^2\\y,z=-np-36\pm q x=6p+8n2y,z=−np−36±q | p = 4 ( n + 3 ) q = ± 4 ( n 2 + 3 n + 9 ) p=4(n+3)\\q=\pm 4(n^2+3n+9) p=4(n+3)q=±4(n2+3n+9) |
| 4 | y / x + z / y + x / z = n y/x+z/y+x/z=n y/x+z/y+x/z=n | q 2 = p 3 + ( n p + 4 ) 2 q^2=p^3+(np+4)^2 q2=p3+(np+4)2 | y / x = − 4 / p z / x = 2 p / ( n p + 4 ± q ) y/x=-4/p\\z/x=2p/(np+4 \pm q) y/x=−4/pz/x=2p/(np+4±q) | p = 0 q = ± 4 p=0\\q=\pm 4 p=0q=±4 |
| 5 | ( x + y + z ) 3 = n x y z (x+y+z)^3=nxyz (x+y+z)3=nxyz | q 2 = p 3 + ( n 2 − 12 n ) p 2 + 48 n 2 p − 64 n 3 q^2=p^3+(n^2-12n)p^2+48n^2p-64n^3 q2=p3+(n2−12n)p2+48n2p−64n3 | x = 8 n 2 y , z = − n p ± q x=8n^2\\y,z=-np\pm q x=8n2y,z=−np±q | p = 4 n q = ± 4 n 2 p=4n\\q=\pm4n^2 p=4nq=±4n2 |
| 6 | x / ( y + z ) + y / ( x + z ) + z / ( x + y ) = n x/(y+z)+y/(x+z)+z/(x+y)= n x/(y+z)+y/(x+z)+z/(x+y)=n | q 2 = p 3 + ( 4 n 2 + 12 n − 3 ) p 2 + 32 ( n + 3 ) p q^2=p^3+(4n^2+12n-3)p^2+32(n+3)p q2=p3+(4n2+12n−3)p2+32(n+3)p | x = 2 ( n + 2 ) p + 8 ( n + 3 ) y , z = p − 8 ( n + 3 ) ± q x=2(n+2)p+8(n+3)\\y,z=p-8(n+3) \pm q x=2(n+2)p+8(n+3)y,z=p−8(n+3)±q | p = 0 , 4 , 8 ( n + 3 ) p=0,4,8(n+3) p=0,4,8(n+3) |
| 7 | ( y + z ) / x + ( x + z ) / y + ( x + y ) / z = n (y+z)/x+(x+z)/y+(x+y)/z=n (y+z)/x+(x+z)/y+(x+y)/z=n | q 2 = p 3 + ( n 2 − 12 ) p 2 + 16 ( n + 3 ) p q^2=p^3+(n^2-12)p^2+16(n+3)p q2=p3+(n2−12)p2+16(n+3)p | x = 2 p − 8 ( n + 3 ) y , z = ( n + 2 ) p ± q x=2p-8(n+3)\\y,z=(n+2)p\pm q x=2p−8(n+3)y,z=(n+2)p±q | p = 0 , 4 , 4 ( n + 3 ) p=0,4,4(n+3) p=0,4,4(n+3) |
第1行的证明:
x
3
+
y
3
=
N
→
换元
(
1
/
u
+
v
)
3
+
(
1
/
u
−
v
)
3
=
2
/
u
3
+
6
v
2
/
u
=
N
→
两边乘
216
N
2
u
3
432
N
2
+
(
36
N
u
v
)
2
=
(
6
N
u
)
3
→
(
36
N
(
x
−
y
)
x
+
y
)
2
=
(
12
N
x
+
y
)
3
−
432
N
2
x^3+y^3=N\\ \xrightarrow{换元}(1/u+v)^3+(1/u-v)^3=2/u^3+6v^2/u=N\\ \xrightarrow{两边乘216N^2u^3}432N^2+(36Nuv)^2=(6Nu)^3\\ \xrightarrow{} (\frac{36N(x-y)}{x+y})^2=(\frac{12N}{x+y})^3-432N^2
x3+y3=N换元(1/u+v)3+(1/u−v)3=2/u3+6v2/u=N两边乘216N2u3432N2+(36Nuv)2=(6Nu)3(x+y36N(x−y))2=(x+y12N)3−432N2
第2行的证明:
a
2
+
b
2
=
c
2
,
n
=
a
b
/
2
→
b
=
2
n
/
a
(
2
n
/
a
)
2
+
a
2
=
c
2
→
两边乘
a
2
4
n
2
+
a
4
=
(
a
c
)
2
=
(
a
2
+
t
)
2
→
展开化简
4
n
2
=
2
a
2
t
+
t
2
→
两边除以
8
(
a
t
/
2
)
2
=
(
−
t
/
2
)
3
−
n
2
(
−
t
/
2
)
→
y
2
=
x
3
−
n
2
x
a^2+b^2=c^2,n=ab/2\\ \xrightarrow{b=2n/a}(2n/a)^2+a^2=c^2\\ \xrightarrow{两边乘a^2}4n^2+a^4=(ac)^2=(a^2+t)^2\\ \xrightarrow{展开化简}4n^2=2a^2t+t^2\\ \xrightarrow{两边除以8}(at/2)^2=(-t/2)^3-n^2(-t/2)\\ \xrightarrow{}y^2=x^3-n^2x
a2+b2=c2,n=ab/2b=2n/a(2n/a)2+a2=c2两边乘a24n2+a4=(ac)2=(a2+t)2展开化简4n2=2a2t+t2两边除以8(at/2)2=(−t/2)3−n2(−t/2)y2=x3−n2x
特别地,
x
4
+
y
4
=
z
4
x^4+y^4=z^4
x4+y4=z4
→
同乘
z
2
/
y
6
x
4
z
2
/
y
6
+
z
2
/
y
2
=
z
6
/
y
6
\xrightarrow{同乘z^2/y^6} x^4z^2/y^6+z^2/y^2=z^6/y^6
同乘z2/y6x4z2/y6+z2/y2=z6/y6
→
(
x
2
z
y
3
)
2
=
(
z
2
y
2
)
3
−
z
2
y
2
\xrightarrow{} (\frac{x^2z}{y^3})^2=(\frac{z^2}{y^2})^3-\frac{z^2}{y^2}
(y3x2z)2=(y2z2)3−y2z2
椭圆曲线上的加法
假如点
P
1
(
x
1
,
y
1
)
、
P
2
(
x
2
,
y
2
)
P_1(x_1,y_1)、P_2(x_2,y_2)
P1(x1,y1)、P2(x2,y2)是椭圆曲线
E
:
y
2
=
x
3
+
a
x
+
b
E:y^2=x^3+ax+b
E:y2=x3+ax+b 上的点,那定义加法为:
P
3
(
x
3
,
y
3
)
=
P
1
(
x
1
,
y
1
)
+
P
2
(
x
2
,
y
2
)
P_3(x_3,y_3)=P_1(x_1,y_1)+P_2(x_2,y_2)
P3(x3,y3)=P1(x1,y1)+P2(x2,y2)
{
x
3
=
t
2
−
x
1
−
x
2
y
3
=
t
(
x
1
−
x
3
)
−
y
1
\begin{cases}x_3=t^2-x_1-x_2\\ y_3=t(x_1-x_3)-y_1\end{cases}
{x3=t2−x1−x2y3=t(x1−x3)−y1
其中
t
=
x
1
2
+
x
1
x
2
+
x
2
2
+
a
y
1
+
y
2
=
{
(
3
x
1
2
+
a
)
/
2
y
1
P
1
=
P
2
(
y
1
−
y
2
)
/
(
x
1
−
x
2
)
P
1
≠
P
2
t=\frac{x_1^2+x_1x_2+x_2^2+a}{y_1+y_2}=\begin{cases} (3x_1^2+a)/2y_1 &P_1 = P_2\\ (y_1-y_2)/(x_1-x_2) &P_1 \ne P_2 \end{cases}
t=y1+y2x12+x1x2+x22+a={(3x12+a)/2y1(y1−y2)/(x1−x2)P1=P2P1=P2
再定义 无穷远点
O
(
∞
,
∞
)
O(\infty,\infty)
O(∞,∞),以及其加法运算
P
+
O
=
O
+
P
=
P
P
(
x
,
y
)
+
P
′
(
x
,
−
y
)
=
O
P+O=O+P=P\\P(x,y)+P'(x,-y)=O
P+O=O+P=PP(x,y)+P′(x,−y)=O
对于
y
2
=
x
3
+
a
x
2
+
b
x
+
c
y^2=x^3+ax^2+bx+c
y2=x3+ax2+bx+c, 则有
{
x
3
=
t
2
−
a
−
x
1
−
x
2
y
3
=
t
(
x
1
−
x
3
)
−
y
1
\begin{cases}x_3=t^2-a-x_1-x_2\\ y_3=t(x_1-x_3)-y_1\end{cases}
{x3=t2−a−x1−x2y3=t(x1−x3)−y1
其中
t
=
(
x
1
+
x
2
)
(
x
1
+
x
2
−
a
)
−
x
1
x
2
+
b
y
1
+
y
2
=
{
(
3
x
1
2
+
2
a
x
1
+
b
)
/
2
y
1
P
1
=
P
2
(
y
1
−
y
2
)
/
(
x
1
−
x
2
)
P
1
≠
P
2
t=\frac{(x_1+x_2)(x_1+x_2-a)-x_1x_2+b}{y_1+y_2}=\begin{cases} (3x_1^2+2ax_1+b)/2y_1 &P_1 = P_2\\ (y_1-y_2)/(x_1-x_2) &P_1 \ne P_2 \end{cases}
t=y1+y2(x1+x2)(x1+x2−a)−x1x2+b={(3x12+2ax1+b)/2y1(y1−y2)/(x1−x2)P1=P2P1=P2
例如:
椭圆曲线
E
0
:
y
2
=
x
3
−
43
x
+
166
E_0:y^2=x^3-43x+166
E0:y2=x3−43x+166 ,
P
(
3
,
8
)
P(3,8)
P(3,8)是
E
0
E_0
E0的一个有理点。
经过加法可以得到其他的有理点。
| 数值 | 图像 |
|---|---|
| P = ( 3 , 8 ) 2 P = P + P = ( − 5 , − 16 ) 3 P = 2 P + P = ( 11 , − 32 ) 4 P = 3 P + P = ( 11 , 32 ) 5 P = 4 P + P = ( − 5 , 16 ) 6 P = 5 P + P = ( 3 , − 8 ) 7 P = 6 P + P = ( ∞ , ∞ ) = O 8 P = 7 P + P = ( 3 , 8 ) = P P=(3,8)\\2P=P+P=(-5,-16)\\3P=2P+P=(11,-32)\\4P=3P+P=(11,32)\\5P=4P+P=(-5,16)\\6P=5P+P=(3,-8)\\7P=6P+P=(\infty,\infty)=O\\8P=7P+P=(3,8)=P P=(3,8)2P=P+P=(−5,−16)3P=2P+P=(11,−32)4P=3P+P=(11,32)5P=4P+P=(−5,16)6P=5P+P=(3,−8)7P=6P+P=(∞,∞)=O8P=7P+P=(3,8)=P | 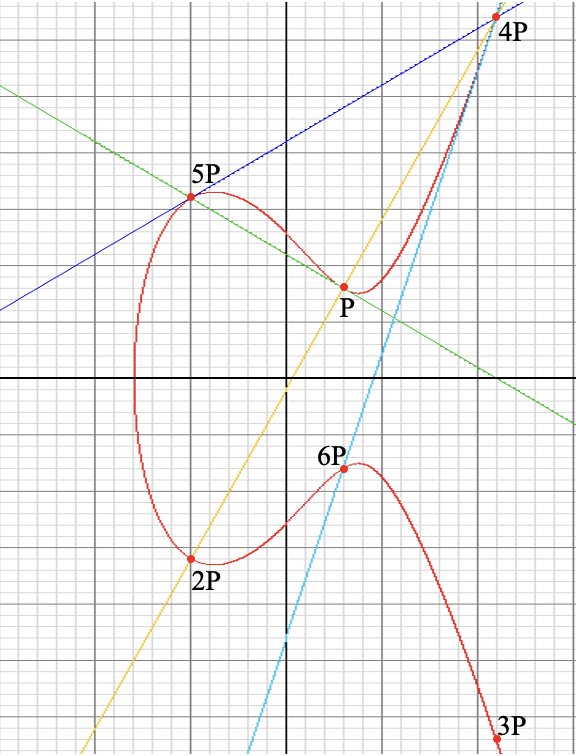 |
加法的作用
- 计算更多有理点。
例如: x 3 + y 3 = 6 x^3+y^3=6 x3+y3=6, 可以转化为 q 2 = p 3 − 2 × 6 5 q^2=p^3-2\times 6^5 q2=p3−2×65, 可以找到整数解 P = ( 28 , 80 ) P=(28,80) P=(28,80),根据加法,得到 2 P = ( 16009 / 100 , − 2021723 / 1000 ) , 3 P = ( 11354888668 / 13209 2 , 1175338498126960 / 13209 3 ) 2P=(16009/100,-2021723/1000),3P=(11354888668/13209^2, 1175338498126960/ 13209^3) 2P=(16009/100,−2021723/1000),3P=(11354888668/132092,1175338498126960/132093)
同时 x , y = ( 216 ± q ) / 6 p x,y=(216\pm q)/6p x,y=(216±q)/6p,得到
( x 1 , y 1 ) = ( 37 / 21 , 17 / 21 ) , ( x 2 , y 2 ) = ( − 1805723 / 960540 , 2237723 / 960540 ) , ( x 3 , y 3 ) = ( 209143555850753 / 112490043311709 , − 84691068680987 / 112490043311709 ) (x_1,y_1)=(37/21,17/21),\\(x_2,y_2)=(-1805723/960540,2237723/960540),\\(x_3,y_3)=(209143555850753/112490043311709,-84691068680987/112490043311709) (x1,y1)=(37/21,17/21),(x2,y2)=(−1805723/960540,2237723/960540),(x3,y3)=(209143555850753/112490043311709,−84691068680987/112490043311709)
可以看到, ( x 3 , y 3 ) (x_3,y_3) (x3,y3)的分母已经是个大数级别,暴力枚举搜索已经无法在短时间内得到。 - 加密算法。
离散对数(ECDLP)问题:在离散椭圆曲线上给定两个点 P P P和 Q Q Q,要求找到一个整数 k k k,其满足 k P = Q kP=Q kP=Q。该问题非常困难,甚至难于大数质因数分解。根据这点可以设计不同的椭圆曲线加密算法。
挠点系与秩
注意到,对于
(
7
n
+
k
)
P
=
k
P
(7n+k)P=kP
(7n+k)P=kP,说明
P
P
P的阶数是7。对于这类阶数有限的点,称为椭圆曲线的挠点。所以
P
(
3
,
8
)
P(3,8)
P(3,8)是椭圆曲线
E
0
:
y
2
=
x
3
−
43
x
+
166
E_0:y^2=x^3-43x+166
E0:y2=x3−43x+166 的7阶挠点。
同时,所有的
{
k
P
}
=
{
O
,
(
3
,
±
8
)
,
(
−
5
,
±
16
)
,
(
11
,
±
32
)
}
\{kP\}=\{O,(3,\pm 8),(-5,\pm 16),(11,\pm 32)\}
{kP}={O,(3,±8),(−5,±16),(11,±32)} 构成一个7阶的循环群,这个群也称为挠点系。
对于另一条椭圆曲线 E 1 : y 2 = x 3 − 16 x + 16 E_1:y^2=x^3-16x+16 E1:y2=x3−16x+16, 可以找到以下有理点
| P | 2P | 3P | 4P | 5P | 6P | 7P | 8P | 9P | 10P |
|---|---|---|---|---|---|---|---|---|---|
| (0,4) | (4,4) | (-4,-4) | (8,-20) | (1,-1) | (24,116) | (-20/9, 172/27) | (84/25, -52/125) | (-80/49, -2108/343) | (161/4, -2033/8) |
| -P | -2P | -3P | -4P | -5P | -6P | -7P | -8P | -9P | -10P |
| (0,-4) | (4,-4) | (-4,4) | (8,20) | (1,1) | (24,-116) | (-20/9, -172/27) | (84/25, 52/125) | (-80/49, 2108/343) | (161/4, 2033/8) |
这里的有理点可以无限加上
(
0
,
4
)
(0,4)
(0,4),而不会出现任何重复。此时我们称为
(
0
,
4
)
(0,4)
(0,4)是
E
1
:
y
2
=
x
3
−
16
x
+
16
E_1:y^2=x^3-16x+16
E1:y2=x3−16x+16的生成元。而且
{
k
P
∣
k
∈
Z
}
\{kP|k\in Z\}
{kP∣k∈Z} 构成一个无限阶的加法群,称为无挠系。
同时,对于
E
1
E_1
E1,所有的有理点都可以用
(
0
,
4
)
(0,4)
(0,4)生成。我们把独立的无挠的生成元的个数,称为椭圆曲线的秩,例如:
- 因为 E 0 E_0 E0不存在无挠的生成元,其秩为0。
- 因为 E 1 E_1 E1只有一个无挠的生成元 ( 0 , 4 ) (0,4) (0,4),其秩为1。
绝大多数椭圆曲线的秩为0或1,但也存在其他数字,例如 E 2 : y 2 = x 3 − 7 x + 10 E_2:y^2=x^3-7x+10 E2:y2=x3−7x+10 的秩为2,因为其有两个独立的无挠生成元 P = ( 1 , 2 ) , Q = ( 3 , 4 ) P=(1,2),Q=(3,4) P=(1,2),Q=(3,4),其有理点可以表示如下(下表包含所有的整数解):
| O | P | 2P | 3P | 4P | 5P | 6P | |
|---|---|---|---|---|---|---|---|
| -2Q | (1/4,-23/8) | (41,-262) | (39/25, 212/125) | (-111/49, -1294/343) | (281/64, -4093/512) | (3169/961, 142174/29791) | (-13529/4761, 865772/328509) |
| -Q | (3,-4) | (5,10) | (-2,4) | (13/9, -46/27) | (67, 548) | (53/121, 3526/1331) | (-30/289, -16090/4913) |
| O | O | (1,2) | (-1,-4) | (0,-26) | (9/4, 19/8) | (-79/25, -94/125) | (439/169, -6716/2197) |
| Q | (3,4) | (-3,2) | (2,-2) | (13,46) | (-5/9, 100/27) | (37/49, -778/343) | (302, -5248) |
| 2Q | (1/4,23/8) | (1/9,-82/27) | (31,-172) | (41/25, 214/125) | (-39/16, -227/64) | (489/121, -9194/1331) | (1871/529, 66068/12167) |
秩为0的椭圆曲线上的有理点个数是有限的。当秩大于0时,可以生成无限多个有理点。
目前还不知道秩有没有上限,现已知最大的秩为 29,对应的椭圆曲线为
y
2
+
x
y
=
x
3
−
27006183241630922218434652145297453784768054621836357954737385
x
+
55258058551342376475736699591118191821521067032535079608372404779149413277716173425636721497
y^2 + xy = x^3 - 27006183241630922218434652145297453784768054621836357954737385x + \ 55258058551342376475736699591118191821521067032535079608372404779149413277716173425636721497
y2+xy=x3−27006183241630922218434652145297453784768054621836357954737385x+ 55258058551342376475736699591118191821521067032535079608372404779149413277716173425636721497
更多信息可以查看History of elliptic curves rank records
关于椭圆曲线的信息,可以查看lmfdb 数据库
相关定理
Mordell-Weil 定理
在Q(有理数域)上,椭圆曲线E的所有有理点构成的群
E
(
Q
)
E(Q)
E(Q),是有限生成Abel群:
E
(
Q
)
=
Z
r
⊕
T
E(Q)=Z^r ⊕ T
E(Q)=Zr⊕T
其中:
r
r
r为E的秩;
T
T
T是挠点系,为有限Abel群。
Mazur 定理
椭圆曲线的挠点系 T T T只能为以下15个群之一:
- Z / n Z Z/nZ Z/nZ,其中 n = 1 , 2 , 3 , . . . , 9 , 10 , o r 12 n=1,2,3,...,9,10,or\ 12 n=1,2,3,...,9,10,or 12
- Z / 2 Z ⊕ Z / 2 n Z Z/2Z ⊕ Z/2nZ Z/2Z⊕Z/2nZ,其中 n = 1 , 2 , 3 , 4 n=1,2,3,4 n=1,2,3,4
例如:
E
0
:
y
2
=
x
3
−
43
x
+
166
E_0:y^2=x^3-43x+166
E0:y2=x3−43x+166 为
Z
/
7
Z
Z/7Z
Z/7Z
E
1
:
y
2
=
x
3
−
16
x
+
16
E_1:y^2=x^3-16x+16
E1:y2=x3−16x+16 为
Z
Z
Z,无挠点系
E
2
:
y
2
=
x
3
−
7
x
+
10
E_2:y^2=x^3-7x+10
E2:y2=x3−7x+10 为
Z
⊕
Z
=
Z
2
Z ⊕ Z=Z^2
Z⊕Z=Z2,无挠点系
Siegel 定理
椭圆曲线上的整数点是有限的。
椭圆曲线求解
求椭圆曲线的有理解比较困难,通常步骤:
- 使用暴力枚举法,找到少量的整数解。
- 根据椭圆曲线加法得到更多的有理解。
除此之外,还可能用到其他的方法:
- 无穷递降法
a 3 + 3 b 3 = 9 c 3 a³+3b³=9c³ a3+3b3=9c3 的整数解
y 2 = x 3 − 2 y^2=x^3-2 y2=x3−2的正整数解 - 群论分析
求 Mordell曲线 y 2 = x 3 + n y^2=x^3+n y2=x3+n 的整数解
求 y 2 = x 3 − 432 y^2=x^3-432 y2=x3−432的有理解
如何证明不定方程(丢番图方程)是否有解?
有些椭圆曲线的证明过程,都可以写成一遍论文。
Mordell曲线: y 2 = x 3 + n y^2=x^3+n y2=x3+n
当n为以下数值时,曲线没有整数解:
6, 7, 11, 13, 14, 20, 21, 23, 29, 32, 34, 39, 42, 45, 46, 47,… oeis.org:
y
2
=
x
3
+
n
y^2=x^3+n
y2=x3+n
-3, -5, -6, -9, -10, -12, -14, -16, -17, -21, -22, -24, -29, -30, -31, -32, -33, -34, -36, -37, -38, -41, -42, -43, -46, -50, … oeis.org:
y
2
=
x
3
−
n
y^2=x^3-n
y2=x3−n
秩的列表如下:
n rank rational_points
1 0 (2,3)[6]
2 1 (-1,1)
3 1 (1,2)
4 0 (0,2)[3]
5 1 (-1,2)
6 0
7 0
8 1 (1,3) x (-2,0)[2]
9 1 (3,6) x (0,3)[3]
10 1 (-1,3)
11 1 (-7/4,19/8)
12 1 (-2,2)
13 0
14 0
15 2 (1,4) x (1/4,31/8)
16 0 (0,4)[3]
17 2 (-2,3) x (4,9)
18 1 (7,19)
19 1 (5,12)
20 0
21 0
22 1 (3,7)
23 0
24 2 (-2,4) x (1,5)
25 0 (0,5)[3]
26 1 (-1,5)
27 0 (-3,0)[2]
28 1 (2,6)
29 0
30 1 (19,83)
-1 0 (1,0)[2]
-2 1 (3,5)
-3 0
-4 1 (2,2)
-5 0
-6 0
-7 1 (2,1)
-8 0 (2,0)
-9 0
-10 0
-11 2 (3,4) x (9/4,5/8)
-12 0
-13 1 (17,70)
-14 0
-15 1 (4,7)
-16 0
-17 0
-18 1 (3,3)
-19 1 (7,18)
-20 1 (6,14)
-21 1 (37/9,188/27)
-22 1 (71/25,119/125)
-23 1 (3,2)
-24 0
-25 1 (5,10)
-26 1 (3,1) x (17/4,57/8)
-27 0 (3,0)[2]
-28 1 (4,6)
-29 1 (3133/9,175364/27)
-30 1 (31/9,89/27)
第三列表示有理数解,不同的生成元单独展示,带[*]表示其为挠点及其阶数




















 621
621

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








