数学笔记-数值计算-多重积分(二)

前言

上一篇已经介绍过一维、三角形、四面体区域的积分。如果积分区域为曲线图形，就要对区域分割成大量的近似三角形（或四面体），计算量将陡增。本篇主要介绍最常见的曲线图形-圆/球 为区域的积分，进入多维积分的世界。

圆周积分

$$\oint (R)={\oint }_{C}f(x,y)ds\approx \frac{C}{N}\sum _{k=1}^{N}f(R\cos \frac{2\pi ik}{N},R\sin \frac{2\pi ik}{N})$$
其中积分区域C为半径为R的圆周，其周长记为$C$(实际上为$2\pi R$)
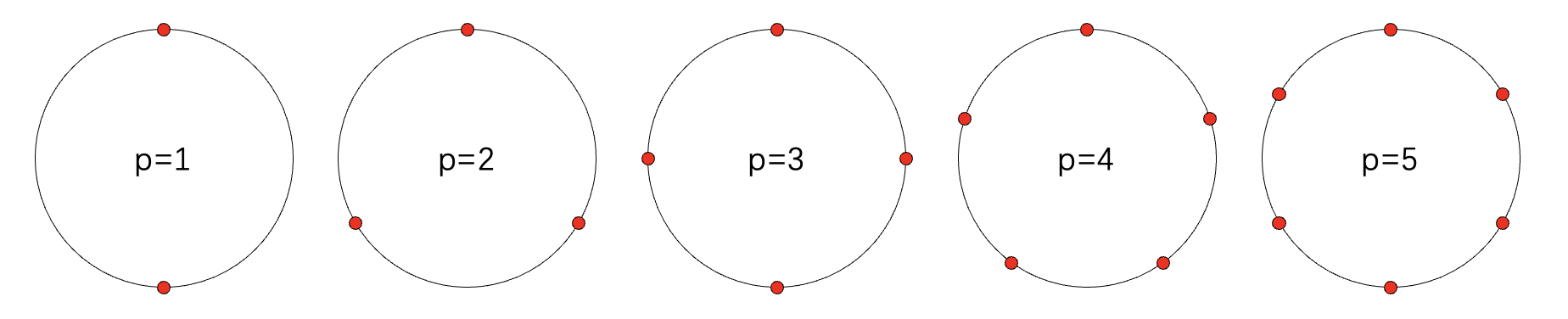
圆周积分较为简单，只需要在圆周上等距离采样，且权重都相等。
当采样数为$N$时，上面的公式的精度为$N-1$.
另外，高斯规则结果等同于等距规则，不再介绍。

圆内积分

$$I_2(R)={\iint }_{D}f(x,y)dS\approx S_D\sum _{i=1}^n{A}_i\oint (r_{i}R)$$
其中积分区域D为半径为R的圆，其面积记为$S_D$(实际上为$\pi R^2$)
$\oint (R)$表示区域为半径R的圆的积分，如果要求$I_2(R)$的精度为p，那可以用精度为p的数值积分值作为代替。
下面为了表示方便，将坐标$(x,y)$记为对应的复数值$x+yi$，并且令 $f(x+yi)=f(x,y)$
同时记第k个N次单位根为 $w_N^k=e^{2\pi ik/N}$

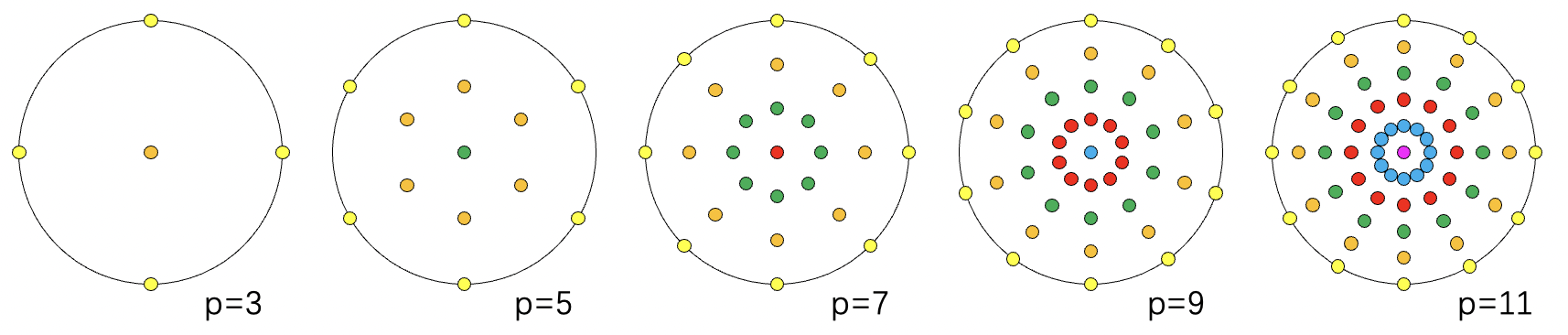
牛顿-柯斯特规则

层数	精度	r	A	样本数
1	1	0	1	1
2	3	$$\begin{gathered} 0 \\ 1 \end{gathered}$$	$$\begin{gathered} 1/2 \\ 1/2 \end{gathered}$$	5
3	5	$$\begin{gathered} 0 \\ 1/2 \\ 1 \end{gathered}$$	$$\begin{gathered} -1/6 \\ 8/9 \\ 5/18 \end{gathered}$$	13
4	7	$$\begin{gathered} 0 \\ 1/3 \\ 2/3 \\ 1 \end{gathered}$$	$$\begin{gathered} 5/16 \\ -9/32 \\ 63/80 \\ 29/160 \end{gathered}$$	25
5	9	$$\begin{gathered} 0 \\ 1/4 \\ 2/4 \\ 3/4 \\ 1 \end{gathered}$$	$$\begin{gathered} -47/90 \\ 704/675 \\ -232/675 \\ 1088/1575 \\ 1249/9450 \end{gathered}$$	41
6	11	$$\begin{gathered} 0 \\ 1/5 \\ 2/5 \\ 3/5 \\ 4/5 \\ 1 \end{gathered}$$	$$\begin{gathered} 8081/6912 \\ -40375/20736 \\ 54625/36288 \\ -43375/96768 \\ 269125/435456 \\ 89581/870912 \end{gathered}$$	61

备注：

• 在此规则下，最外2层的符号为正，最外第3次变负号开始，每往内一层都改变符号。
• 总层数增加时，最外层的权重为正，但向0递减。
• 采样点如下，其中权重值按 紫红>红>橙>黄>0>绿>蓝 来设置颜色。
  

高斯规则

r 是 Zernike多项式 的零点，且有：
$$\begin{gathered} Z_n(x)=\sum _{k=0}^{\lfloor n/2\rfloor }\frac{(-1{)}^k(n-k)!x^{n-2k}}{k!(\lceil \frac{n}{2}\rceil -k)!(\lfloor \frac{n}{2}\rfloor -k)!}=\sum _{k=0}^n{Z}_n^k{x}^k \\ {A}_{2n}(x)=\frac{2}{Z_n^{\prime }(x)}\sum _{k=0}^{n-1}\sum _{m=1}^{n-k}\frac{Z_{2n}^{2m+2k}}{m}{x}^{2k+1} \\ {A}_{2n+1}(x)=\frac{2}{Z_n^{\prime }(x)}\sum _{k=0}^{n-1}\sum _{m=1}^{n-k}\frac{Z_{2n+1}^{2m+2k+1}}{m+1}{x}^{2k},(x\ne 0) \\ {A}_{2n+1}(0)=\frac{4}{(n+1{)}^2} \end{gathered}$$
这里有

• $A_n(x)=\frac{4}{(1-x^2)F_n^{\prime }(x{)}^2},A_{2n-1}(0)=1/n^2$
• ${\int }_0^{1}x{Z}_n(x)Z_{n+2k}(x)dx=0,(k\in Z,k\ne 0)$
• ${\int }_0^{1}x{Z}_n(x{)}^{2}dx=\frac{1}{2n+2}$

这里要求 $N\ge 2n$, 此时公式的精度为$2n-1$。如果$N=2n-1$，则公式精度为$2n-2$。

例如 n=3时，取N=6，有
$$I\approx S_D[\frac{1}{4}f(0)+\frac{3}{4\times 6}\sum _{k=1}^{6}f(\frac{\sqrt{6}}{3}{e}^{2\pi ik/6})]$$
需要7个采样点，精度为5，即$f(x,y)$的次数不大于5时，公式的误差为0。
另外，因为N并不固定，当n=4时，还可以有以下形式：
$$I\approx S_D[\frac{1}{2\times 8}\sum _{k=1}^{8}f(\sqrt{\frac{3-\sqrt{3}}{6}}{e}^{2\pi ik/8})+\frac{1}{2\times 9}\sum _{k=1}^{9}f(\sqrt{\frac{3+\sqrt{3}}{6}}{e}^{2\pi ik/9})]$$
但这样就需要采集8+9=17个样本。而且因为不论N取多大，精度都不会提升，所以不如直接取(8,8)，这样就需要最少的样本数16。

更多数值如下：

n	Zernike多项式	$r_i$	$A_i$	最少采样数	精度
1	$Z=r$	0	1	1	1
2	$Z=2r^2-1$	$\sqrt{2}/2=0.7071067812$	1	4	3
3	$Z=3r^3-2r$	$$\begin{gathered} 0 \\ \sqrt{6}/3=0.8164965809 \end{gathered}$$	$$\begin{gathered} 1/4 \\ 3/4 \end{gathered}$$	7	5
4	$Z=6r^4-6r^2+1$	$$\begin{gathered} \sqrt{(3-\sqrt{3})/6}=0.4597008434 \\ \sqrt{(3+\sqrt{3})/6}=0.8880738340 \end{gathered}$$	$$\begin{gathered} 1/2 \\ 1/2 \end{gathered}$$	16	7
5	$Z=10r^5-12r^3+3r$	$$\begin{gathered} 0 \\ \sqrt{(6-\sqrt{6})/10}=0.5958615827 \\ \sqrt{(6+\sqrt{6})/10}=0.9192110608 \end{gathered}$$	$$\begin{gathered} 1/9=0.1111111111 \\ (16+\sqrt{6})/36=0.5124858262 \\ (16-\sqrt{6})/36=0.3764030627 \end{gathered}$$	21	9
6	$Z=20r^6-30r^4+12r^2-1$	$$\begin{gathered} \sqrt{(5-\sqrt{15})/10}=0.3357106870 \\ \sqrt{2}/2=0.7071067812 \\ \sqrt{(5+\sqrt{15})/10}=0.9419651451 \end{gathered}$$	$$\begin{gathered} 5/18=0.2777777777 \\ 4/9=0.4444444444 \\ 5/18=0.2777777777 \end{gathered}$$	36	11
7	$Z=35r^7-60r^5+30r^3-4r$	$$\begin{gathered} 0 \\ 0.4608042298 \\ 0.7684615381 \\ 0.9546790248 \end{gathered}$$	$$\begin{gathered} 1/16=0.0625 \\ 0.3288443200 \\ 0.3881934688 \\ 0.2204622112 \end{gathered}$$	43	13
8	$Z=70r^8-140r^6+90r^4-20r^2+1$	$$\begin{gathered} 0.2634992300 \\ 0.5744645143 \\ 0.8185294874 \\ 0.9646596062 \end{gathered}$$	$$\begin{gathered} (18-\sqrt{30})/72=0.1739274226 \\ (18+\sqrt{30})/72=0.3260725774 \\ (18+\sqrt{30})/72=0.3260725774 \\ (18-\sqrt{30})/72=0.1739274226 \end{gathered}$$	64	15

球面积分

$$\iint (R)=\iint f(x,y)dS=S_D\sum _{k=1}^N{A}_{k}f(x_k,y_k,z_k)$$
其中积分区域D为半径为R的球面，其面积记为$S_D$(实际上为$4\pi R^2$)

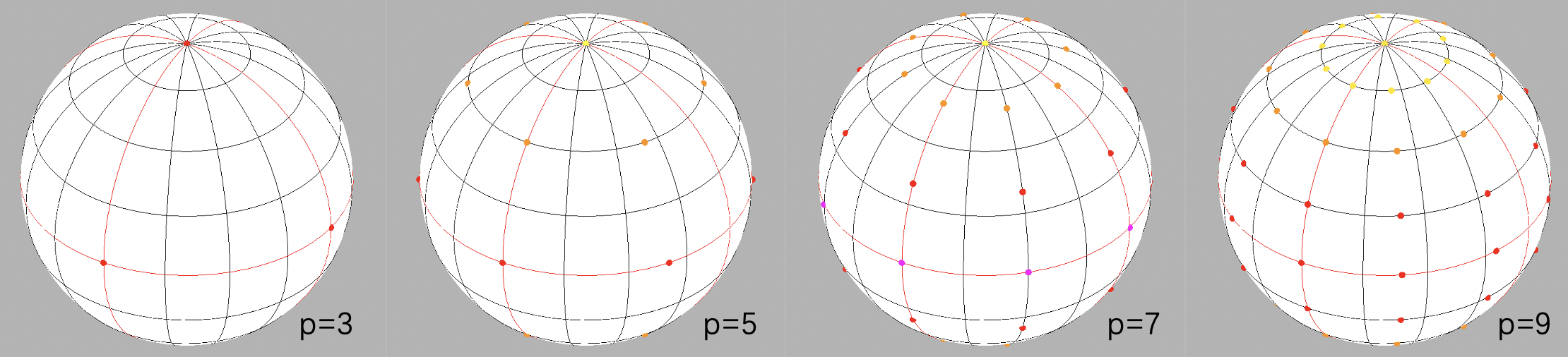
牛顿-柯斯特规则

精度	经度	纬度	权重	最少样本数
3	$2\pi k/4$	$$\begin{gathered} 0 \\ \pm \pi /2 \end{gathered}$$	$$\begin{gathered} 2/3 \\ 1/6 \end{gathered}$$	6
5	$2\pi k/6$	$$\begin{gathered} 0 \\ \pm \pi /4 \\ \pm 2\pi /4 \end{gathered}$$	$$\begin{gathered} 2/5=0.4 \\ 4/15=0.2666667 \\ 1/30=0.0333333 \end{gathered}$$	20
7	$2\pi k/8$	$$\begin{gathered} 0 \\ \pm \pi /6 \\ \pm 2\pi /6 \\ \pm 3\pi /6 \end{gathered}$$	$$\begin{gathered} 82/315=0.2603175 \\ 8/35=0.2285714 \\ 8/63=0.1269841 \\ 1/70=0.0142857 \end{gathered}$$	42
9	$2\pi k/10$	$$\begin{gathered} 0 \\ \pm \pi /8 \\ \pm 2\pi /8 \\ \pm 3\pi /8 \\ \pm 4\pi /8 \end{gathered}$$	$$\begin{gathered} 62/315=0.1968254 \\ (40+12\sqrt{2})/315=0.1808589 \\ 44/315=0.1396825 \\ (40-12\sqrt{2})/315=0.0731093 \\ 1/126=0.0079365 \end{gathered}$$	72
11	$2\pi k/12$	$$\begin{gathered} 0 \\ \pm \pi /10 \\ \pm 2\pi /10 \\ \pm 3\pi /10 \\ \pm 4\pi /10 \\ \pm 5\pi /10 \end{gathered}$$	$$\begin{gathered} 302/1925=0.1568831 \\ (420+44\sqrt{5})/3465=0.1496066 \\ (1508+308\sqrt{5})/17325=0.1267942 \\ (420-44\sqrt{5})/3465=0.0928176 \\ (1508-308\sqrt{5})/17325=0.0472895 \\ 1/198=0.0050505 \end{gathered}$$	101
13	$2\pi k/14$	$$\begin{gathered} 0 \\ \pm \pi /12 \\ \pm 2\pi /12 \\ \pm 3\pi /12 \\ \pm 4\pi /12 \\ \pm 5\pi /12 \\ \pm 6\pi /12 \end{gathered}$$	$$\begin{gathered} 17702/135135=0.1309949 \\ 8(1346+455\sqrt{3})/135135=0.1263378 \\ 568/5005=0.1134865 \\ 12484/135135=0.0923817 \\ 808/12285=0.0657713 \\ 8(1346-455\sqrt{3})/135135=0.0330287 \\ 1/286=0.0034965 \end{gathered}$$	145

备注：

1. 上表中, 经度数=精度+1。
2. 选择不同的经度数，实际权重（两个极点除外）需要除以经度数。例如：精度=3时，取经度数=4，两个极点权重保持不变(1/6), 其他的节点的权重$=2/3÷4=1/6$, 这时节点刚好构成正八面体，且所有节点权重都相等。

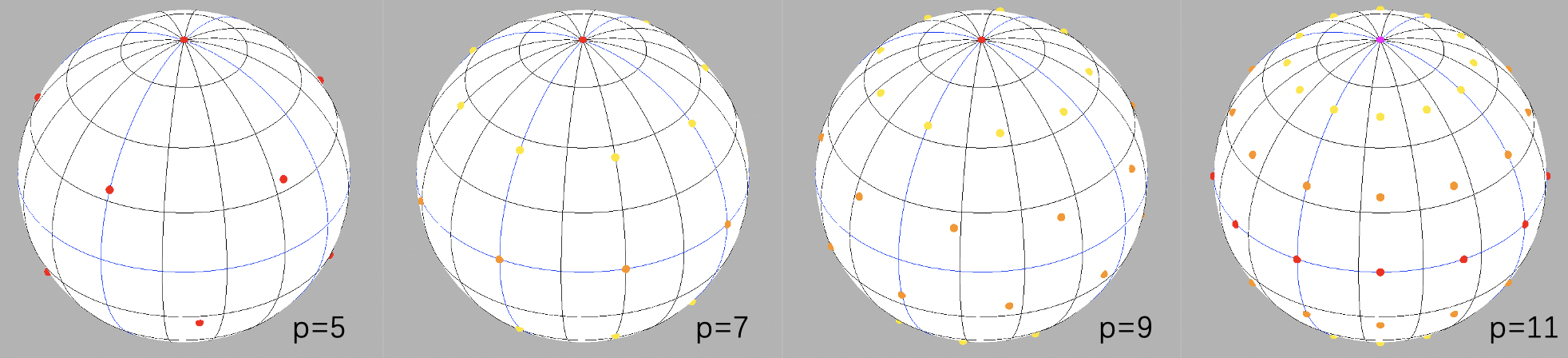
高斯规则（平行同心圆）

n	特征多项式 $F_n(x)$	纬度w	权重A	经度	样本数	精度
1	$x$	$$\begin{gathered} 0 \\ \pm \pi /2 \end{gathered}$$	$$\begin{gathered} 2/3 \\ 1/6 \end{gathered}$$	$2k\pi /4$	6	3
2	$(5x^2-1)/4$	$$\begin{gathered} \pm 0.4636476090=26.565^{\circ } \\ \pm \pi /2 \end{gathered}$$	$$\begin{gathered} 5/12 \\ 1/12 \end{gathered}$$	$2k\pi /5^{\ast }$	12	5
3	$(7x^3-3x)/4$	$$\begin{gathered} 0 \\ \pm 0.7137243789=40.893^{\circ } \\ \pm \pi /2 \end{gathered}$$	$$\begin{gathered} 16/45 \\ 49/180 \\ 1/20 \end{gathered}$$	$2k\pi /8$	26	7
4	$(21x^4-14x^2+1)/8$	$$\begin{gathered} \pm 0.2892479703=16.573^{\circ } \\ \pm 0.8711272375=49.912^{\circ } \\ \pm \pi /2 \end{gathered}$$	$$\begin{gathered} 0.2774291885 \\ 0.1892374781 \\ 1/30=0.0333333333 \end{gathered}$$	$2k\pi /9^{\ast }$	38	9
5	$(33x^5-30x^3+5x)/8$	$$\begin{gathered} 0 \\ \pm 0.4879869928=27.960^{\circ } \\ \pm 0.9795092224=56.122^{\circ } \\ \pm \pi /2 \end{gathered}$$	$$\begin{gathered} 128/525=0.2438095238 \\ 0.2158726906 \\ 0.1384130237 \\ 1/42=0.0238095238 \end{gathered}$$	$2k\pi /12$	62	11
6	$(429x^6-495x^4+135x^2-5)/64$	$$\begin{gathered} \pm 0.2108582499=12.081^{\circ } \\ \pm 0.6331662051=36.278^{\circ } \\ \pm 1.0587427294=60.661^{\circ } \\ \pm \pi /2 \end{gathered}$$	$$\begin{gathered} 0.2062293973 \\ 0.1705613462 \\ 0.1053521136 \\ 1/56=0.01785714286 \end{gathered}$$	$2k\pi /13^{\ast }$	80	13
7	$(715x^7-1001x^5+385x^3-35x)/64$	$$\begin{gathered} 0 \\ \pm 0.3716115607=21.292^{\circ } \\ \pm 0.7439319041=42.624^{\circ } \\ \pm 1.1192146362=64.126^{\circ } \\ \pm \pi /2 \end{gathered}$$	$$\begin{gathered} 2048/11025=0.1857596372 \\ 0.1732142555 \\ 0.1372693563 \\ 0.0827476808 \\ 1/72=0.0138888889 \end{gathered}$$	$2k\pi /16$	114	15
8	$(2431x^8-4004x^6+2002x^4-308x^2+7)/128$	$$\begin{gathered} \pm 0.1660408523=9.513^{\circ } \\ \pm 0.4982908852=28.550^{\circ } \\ \pm 0.8312492225=47.627^{\circ } \\ \pm 1.1668928829=66.858^{\circ } \\ \pm \pi /2 \end{gathered}$$	$$\begin{gathered} 0.1637698806 \\ 0.1460213418 \\ 0.1124446710 \\ 0.0666529954 \\ 1/90=0.0111111111 \end{gathered}$$	$2k\pi /17^{\ast }$	138	17
9	$(4199x^9-7956x^7+4914x^5-1092x^3+63x)/128$	$$\begin{gathered} 0 \\ \pm 0.3002490621=17.203^{\circ } \\ \pm 0.6007184949=34.419^{\circ } \\ \pm 0.9018627818=51.673^{\circ } \\ \pm 1.2054537685=69.067^{\circ } \\ \pm \pi /2 \end{gathered}$$	$$\begin{gathered} 32768/218295=0.1501087977 \\ 0.1434395624 \\ 0.1240240521 \\ 0.0935849409 \\ 0.0548061366 \\ 1/110=0.0090909091 \end{gathered}$$	$2k\pi /20$	182	19

备注：

• 纬度值w为方程 $F(\sin (w))=0$ 的解，例如 $5{\sin }^2(26.565^{\circ })-1=0$
• 经度数j至少为精度p。如果$p=4Z+1$,那么可以使经度数$j=p-1$，此时要求当纬度值为正时，取经度$2k\pi /j$，为负时取经度$(2k+1)\pi /j$
• 上述表格中，精度3对应正八面体，精度5对应正二十面体。
• $A_n(x)=\frac{4}{(n+1)(n+2)[(x^2-1)F_n^{\prime }(x){]}^2}，A_n(\pm 1)=\frac{1}{(n+1)(n+2)}$
• ${\int }_{-1}^1(1-x^2)F_k(x)F_n(x)dx=0,(k\ne n)$
• ${\int }_{-1}^1(1-x^2)F_n(x{)}^{2}dx=\frac{32}{(2n+2)(2n+3)(2n+4)}$
• 这里强制带上了2个极点，如果不带极点，那结论会和 高斯-勒让德 规则一样，但样本数要多于带极点情况，因此不做讨论。

正多面体规则

如果按正多面体的顶点来采样，因对称性，每个顶点的权重都相等。

	正四面体	正八面体	正方体	正二十面体	正十二面体	截角正八面体
顶点数	4	6	8	12	20	48
精度	2	3	3	5	5	7

备注：

• 正多面体只有5种，无法扩展，无法得到更高精度的公式。
• 表中的截角正八面体，顶点为$perm(\pm 0.2666354015,\pm 0.4225186538,\pm 0.8662468181)$ (perm表示对参数全排列)，这些分量都为方程$105x^6-105x^4+21x^2-1=0$的根。

Lebedev 规则

此规则由 Vyacheslav Lebedev 提出，具体可以查看以下文献：
Quadrature Cubed Sphere
sphere_lebedev_rule

精度	样本数	子样本数	坐标	权重
3	6	6	$0,0,1$	$1/6=0.166666667$
5	14	$$\begin{gathered} 6 \\ 8 \end{gathered}$$	$$\begin{gathered} 0,0,1 \\ 0.577350269,0.577350269,0.577350269 \end{gathered}$$	$$\begin{gathered} 1/15=0.066666667 \\ 3/40=0.075 \end{gathered}$$
7	26	$$\begin{gathered} 6 \\ 8 \\ 12 \end{gathered}$$	$$\begin{gathered} 0,0,1 \\ 0.577350269,0.577350269,0.577350269 \\ 0,0.707106781,0.707106781 \end{gathered}$$	$$\begin{gathered} 1/21=0.047619048 \\ 4/105=0.038095238 \\ 9/280=0.032142857 \end{gathered}$$
9	38	$$\begin{gathered} 6 \\ 8 \\ 24 \end{gathered}$$	$$\begin{gathered} 0,0,1 \\ 0.577350269,0.577350269,0.577350269 \\ 0,0.459700843,0.888073834 \end{gathered}$$	$$\begin{gathered} 1/105=0.009523810 \\ 9/280=0.032142857 \\ 1/35=0.028571429 \end{gathered}$$
11	50	$$\begin{gathered} 6 \\ 8 \\ 12 \\ 24 \end{gathered}$$	$$\begin{gathered} 0,0,1 \\ 0.577350269,0.577350269,0.577350269 \\ 0,0.707106781,0.707106781 \\ 0.301511345,0.301511345,0.904534034 \end{gathered}$$	$$\begin{gathered} 8/630=0.012698413 \\ 27/1280=0.021093750 \\ 64/2835=0.022574956 \\ 14641/725760=0.020173336 \end{gathered}$$
13	74	$$\begin{gathered} 6 \\ 8 \\ 12 \\ 24 \\ 24 \end{gathered}$$	$$\begin{gathered} 0,0,1 \\ 0.577350269,0.577350269,0.577350269 \\ 0,0.707106781,0.707106781 \\ 0.480384461,0.480384461,0.733799386 \\ 0,0.320772649,0.947156221 \end{gathered}$$	$$\begin{gathered} 0.00051306718 \\ -0.02958603896 \\ 0.01660406957 \\ 0.02657620708 \\ 0.01652217099 \end{gathered}$$
15	86	$$\begin{gathered} 6 \\ 8 \\ 24 \\ 24 \\ 24 \end{gathered}$$	$$\begin{gathered} 0,0,1 \\ 0.577350269,0.577350269,0.577350269 \\ 0.369602846,0.369602846,0.852518312 \\ 0.694354007,0.694354007,0.189063553 \\ 0,0.374243039,0.927330657 \end{gathered}$$	$$\begin{gathered} 0.01154401154 \\ 0.01194390909 \\ 0.01111055571 \\ 0.01187650129 \\ 0.01181230375 \end{gathered}$$

备注：

• 对所有精度： $0.577350269=\sqrt{1/3},0.707106781=\sqrt{1/2}$
• 精度9： $0.459700843,0.888073834=\sqrt{(3\mp \sqrt{3})/6}$
• 精度11：$0.301511345=\sqrt{1/11},0.904534034=\sqrt{3/11}$
• 精度13：$0.480384461=\sqrt{3/13},0.733799386=\sqrt{7/13}$
  $0.320772649,0.947156221=\sqrt{(65\mp \sqrt{2665})/130}$
• 精度15：$0.374243039,0.927330657=\sqrt{(39\mp \sqrt{78\sqrt{13}+507})/78}$

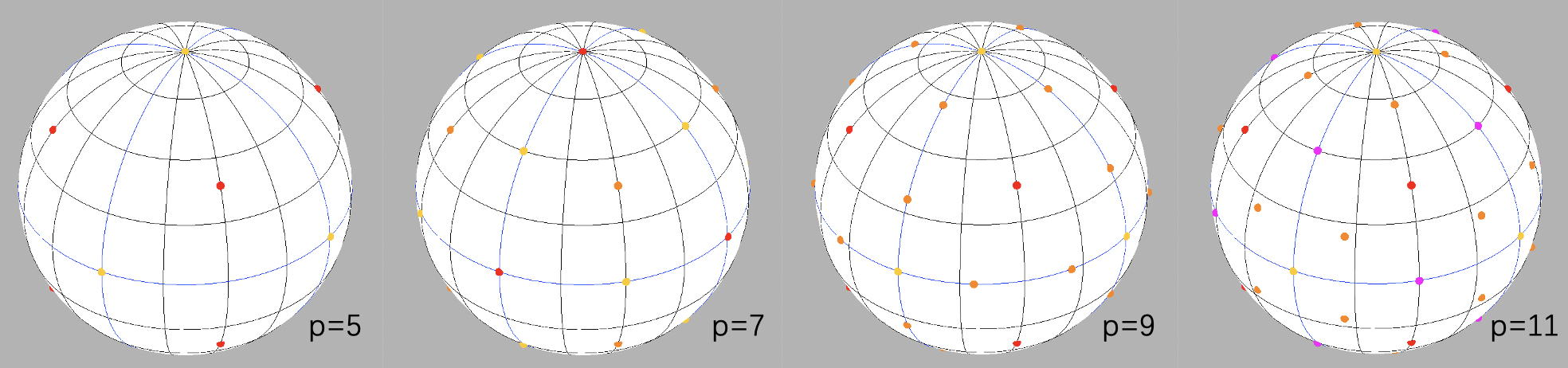
与前面的其他积分规则相比， Lebedev 规则在同等精度下(除了精度5)，所需要的样本数都是最少的。这也是后面球内积分首选的球内积分规则。

球内积分

$$I_3(R)={\iiint }_{D}f(x,y,z)dV=V_D\sum _{i=1}^n{A}_i\iint (r_{i}R)$$
其中积分区域D为半径为R的球，其体积记为$V_D$(实际上为$4\pi R^3/3$)
$\iint (R)$表示区域为半径R的球面的积分，可以用与$I_3(R)$精度相同的数值积分值作为代替。根据上述结论，可以用Lebedev 规则来计算球面积分。

牛顿-柯斯特规则

层数	精度	r	A	采样数
1	1	0	1	1
2	3	$$\begin{gathered} 0 \\ 1 \end{gathered}$$	$$\begin{gathered} 2/5 \\ 3/5 \end{gathered}$$	7
3	5	$$\begin{gathered} 0 \\ 1/2 \\ 1 \end{gathered}$$	$$\begin{gathered} -2/7 \\ 32/35 \\ 13/35 \end{gathered}$$	25
4	7	$$\begin{gathered} 0 \\ 1/3 \\ 2/3 \\ 1 \end{gathered}$$	$$\begin{gathered} 2/5 \\ -81/140 \\ 162/175 \\ 177/700 \end{gathered}$$	79
5	9	$$\begin{gathered} 0 \\ 1/4 \\ 2/4 \\ 3/4 \\ 1 \end{gathered}$$	$$\begin{gathered} -74/99 \\ 69376/51975 \\ -33632/51975 \\ 15104/17325 \\ 9769/51975 \end{gathered}$$	153
6	11	$$\begin{gathered} 0 \\ 1/5 \\ 2/5 \\ 3/5 \\ 4/5 \\ 1 \end{gathered}$$	$$\begin{gathered} 26927/16380 \\ -614975/216216 \\ 126275/63063 \\ -769025/1009008 \\ 1843925/2270268 \\ 6718091/45405360 \end{gathered}$$	251

高斯规则

n	特征多项式 $F_n(r)$	$r_i$	$A_i$	精度	最少采样数
1	$r$	0	1	1	1
2	$(5r^2-3)/2$	$0.7745966692$	1	3	6
3	$(7r^3-5r)/2$	$$\begin{gathered} 0 \\ 0.8451542547 \end{gathered}$$	$$\begin{gathered} 4/25=0.16 \\ 21/25=0.84 \end{gathered}$$	5	13
4	$(63r^4-70r^2+15)/8$	$$\begin{gathered} 0.5384693101 \\ 0.9061798459 \end{gathered}$$	$$\begin{gathered} 0.4163339973 \\ 0.5836660027 \end{gathered}$$	7	52
5	$(99r^5-126r^3+35r)/8$	$$\begin{gathered} 0 \\ 0.6399972828 \\ 0.9290483038 \end{gathered}$$	$$\begin{gathered} 64/1225=0.0522448980 \\ 0.4807499830 \\ 0.4670051191 \end{gathered}$$	9	77
6	$(429r^6-693r^4+315r^2-35)/16$	$$\begin{gathered} 0.4058451514 \\ 0.7415311856 \\ 0.9491079123 \end{gathered}$$	$$\begin{gathered} 0.1886740115 \\ 0.4614035515 \\ 0.3499224370 \end{gathered}$$	11	150
7	$(715r^7-1287r^5+693r^3-105r)/16$	$$\begin{gathered} 0 \\ 0.5056316101 \\ 0.7901728521 \\ 0.9591472977 \end{gathered}$$	$$\begin{gathered} 256/11025=0.0232199546 \\ 0.2573443778 \\ 0.4318411585 \\ 0.2875945090 \end{gathered}$$	13	223
8	$(12155r^8-25740r^6+18018r^4-4620r^2+315)/128$	$$\begin{gathered} 0.3242534234 \\ 0.6133714327 \\ 0.8360311073 \\ 0.9681602395 \end{gathered}$$	$$\begin{gathered} 0.0985207798 \\ 0.2941443981 \\ 0.3787910186 \\ 0.2285438034 \end{gathered}$$	15	344

这里有：

• $A_n(x)=\frac{6}{(1-x^2)F_n^{\prime }(x{)}^2}$
• ${\int }_0^1{x}^2{F}_n(x)F_{n+2k}(x)dx=0,(k\in Z,k\ne 0)$
• ${\int }_0^1{x}^2{F}_n(x{)}^{2}dx=\frac{1}{2n+3}$

附录：相关定积分公式

单位圆周

记 $I_{\Omega }(p,q)={\iint }_{\Omega }{x}^p{y}^{q}ds$, $\Omega$是单位圆周。有：
$$\begin{gathered} I_{\Omega }(p,q)=I_{\Omega }(q,p) \\ {I}_{\Omega }(p,q)=\frac{p-1}{p+q}{I}_{\Omega }(p-2,q),p\ge 2 \\ {I}_{\Omega }(0,0)=2\pi \end{gathered}$$
如果 $p,q$ 存在奇数，则$I_{\Omega }(p,q)=0$

单位球面

记 $I_{\Omega }(p,q,r)={\iint }_{\Omega }{x}^p{y}^q{z}^{r}dS$, $\Omega$是单位球面。有：
$$\begin{gathered} I_{\Omega }(p,q,r)=I_{\Omega }(q,p,r)=I_{\Omega }(p,r,q) \\ {I}_{\Omega }(p,q,r)=\frac{p-1}{p+q+r+1}{I}_{\Omega }(p-2,q,r),p\ge 2 \\ {I}_{\Omega }(0,0,0)=4\pi \end{gathered}$$
如果 $p,q,r$ 存在奇数，则$I_{\Omega }(p,q,r)=0$

单位圆

记 $I_{\odot }(p,q)={\iint }_{\odot }{x}^p{y}^{q}dS$,$\odot$是单位圆。有：
$$\begin{gathered} I_{\odot }(p,q)=I_{\odot }(q,p) \\ {I}_{\odot }(p,q)=\frac{p-1}{p+q+2}{I}_{\Omega }(p-2,q)，p\ge 2 \\ {I}_{\odot }(0,0)=\pi \end{gathered}$$
如果 $p,q$ 存在奇数，则$I_{\odot }(p,q)=0$

单位球

记 $I_{\odot }(p,q,r)={\iiint }_{\odot }{x}^p{y}^q{z}^{r}dV$,$\odot$是单位球。有：
$I_{\odot }(p,q,r)=I_{\odot }(q,p,r)=I_{\odot }(p,r,q)$
$I_{\odot }(p,q,r)=\frac{p-1}{p+q+r+3}{I}_{\odot }(p-2,q,r)，p\ge 2$
$I_{\odot }(0,0,0)=4\pi /3$
如果 $p,q,r$ 存在奇数，则$I_{\odot }(p,q,r)=0$

相关Python代码如下：

import sympy

# 圆周
def integrate_circle(p, q):
    if p % 2 == 1 or q % 2 == 1:
    	return 0
    if p == 0:
        if q == 0:
        	return sympy.pi*2
        return integrate_circle(q, 0)
    return integrate_circle(p-2, q)*(p-1)/(p+q)

# 球面
def integrate_sphere_face(p, q, r):
    if p % 2 == 1 or q % 2 == 1 or r % 2 == 1:
    	return 0
    if p == 0:
        if q == 0 and r == 0:
            return sympy.pi*4
        return integrate_sphere_face(q, r, 0)
    return integrate_sphere_face(p-2, q, r)*(p-1)/(p+q+r+1)

# 圆内
def integrate_disk(p, q):
    if p % 2 == 1 or q % 2 == 1:
    	return 0
    if p == 0:
        if q == 0:
        	return sympy.pi
        return integrate_disk(q, 0)
    return integrate_disk(p-2, q)*(p-1)/(p+q+2)

# 球内
def integrate_sphere(p, q, r):
    if p % 2 == 1 or q % 2 == 1 or r % 2 == 1:
    	return 0
    if p == 0:
        if q == 0 and r == 0:
            return sympy.pi*4/3
        return integrate_sphere(q, r, 0)
    return integrate_sphere(p-2, q, r)*(p-1)/(p+q+r+3)