【Eigen教程】数值优化（九）

第9章 数值优化

• 优化中的牛顿法

• 高斯 - 牛顿算法

  • 高斯 - 牛顿法示例，逆运动学问题

• 非线性最小二乘法（曲线拟合）

• 非线性回归

• 非线性回归与非线性拟合的区别

• 列文伯格 - 马夸尔特算法

优化中的牛顿法

高斯 - 牛顿算法

高斯 - 牛顿算法是牛顿法的一种改进，用于寻找函数的最小值。

与牛顿法不同，它不需要二阶导数（二阶导数可能较难计算）。

参考文献：https://math.stackexchange.com/questions/19948/pseudoinverse-matrix-and-svd 

高斯 - 牛顿法示例，逆运动学问题

接下来我们将求解一个三连杆平面机器人的逆运动学问题。

这段C++代码主要涉及正向运动学和逆运动学计算。它使用Eigen库处理矩阵和几何变换，定义了多个类型和函数模板，提供了数值微分功能，并实现了目标函数，计算机器人末端执行器在二维平面上的位置和姿态。

主要内容概括：

1. 包含的库

   ：包括数学、输入输出流以及Eigen库的密集矩阵运算、几何运算和数值微分头文件。

2. 类型定义

   ：定义了向量类型、矩阵类型和二维仿射变换类型。

3. 函数声明

   ：

• forward_kinematics

  ：正向运动学函数。

• pseudoInverse

  ：伪逆函数模板。

• transformationMatrixToPose

  ：将变换矩阵转换为姿态的函数。

• distanceError

  ：计算距离误差函数。

• inverse_kinematics

  ：逆运动学函数（两种形式）。

结构体

：

• Functor

  ：一个通用的函数对象结构体，定义了输入和输出类型及其维度。

• numericalDifferentiationFKFunctor

  ：数值微分正向运动学函数对象，实现了具体的目标函数，计算机器人末端在平面上的位置（x,y）和旋转角度（theta）。

辅助函数模板

：

• signum

  ：符号函数模板，处理符号类型和非符号类型。

• normaliseAngle

   和 normaliseAngle2：角度归一化函数模板。

这段代码可以用于机器人运动学计算，特别是涉及到正向和逆向的运动学问题。

task.hpp

#include <math.h> // 包含数学库的头文件
#include <iostream> // 包含输入输出流的头文件
#include <Eigen/Dense> // 包含Eigen库的密集矩阵运算头文件
#include <Eigen/Geometry> // 包含Eigen库的几何运算头文件
#include <eigen3/unsupported/Eigen/NumericalDiff> // 包含Eigen库不支持的数值微分头文件

typedef Eigen::VectorXd vector_t;// 定义向量类型
typedef Eigen::MatrixXd matrix_t;// 定义矩阵类型
typedef Eigen::Transform<double,2,Eigen::Affine> trafo2d_t;// 定义二维仿射变换类型

trafo2d_t forward_kinematics(vector_t const& q );// 声明正向运动学函数

template<typenameT>
T pseudoInverse(const T &a,double epsilon = std::numeric_limits<double>::epsilon());// 声明伪逆函数模板

template<typename_Scalar,int NX = Eigen::Dynamic,int NY = Eigen::Dynamic>
structFunctor
{
    typedef _Scalar Scalar;// 定义标量类型
    enum{
        InputsAtCompileTime = NX,// 编译时输入维度
        ValuesAtCompileTime = NY // 编译时输出维度
    };

    typedef Eigen::Matrix<Scalar,InputsAtCompileTime,1> InputType;// 输入类型
    typedef Eigen::Matrix<Scalar,ValuesAtCompileTime,1> ValueType;// 输出类型
    typedef Eigen::Matrix<Scalar,ValuesAtCompileTime,InputsAtCompileTime> JacobianType;// 雅可比类型

    int m_inputs, m_values;// 输入和输出维度

    Functor():m_inputs(InputsAtCompileTime),m_values(ValuesAtCompileTime){}// 默认构造函数
    Functor(int inputs,int values):m_inputs(inputs),m_values(values){}// 参数化构造函数

    intinputs()const{return m_inputs;}// 获取输入维度
    intvalues()const{return m_values;}// 获取输出维度
};

structnumericalDifferentiationFKFunctor:Functor<double>
{
    numericalDifferentiationFKFunctor():Functor<double>(3,3){}// 简单构造函数

    intoperator()(const Eigen::VectorXd &q, Eigen::VectorXd &fvec)const// 实现目标函数
    {
        trafo2d_t t =forward_kinematics(q);// 调用正向运动学函数
        double theta =atan2(t.rotation()(1,0),t.rotation()(0,0));// 计算旋转角度
        double x = t.translation()(0);// 获取平移X分量
        double y = t.translation()(1);// 获取平移Y分量

        fvec(0)= x;// 设置输出向量X分量
        fvec(1)= y;// 设置输出向量Y分量
        fvec(2)= theta;// 设置输出向量旋转角度

        return0;// 返回成功状态
    }
};

Eigen::MatrixXd numericalDifferentiationFK(const Eigen::VectorXd &q);// 声明数值微分正向运动学函数

Eigen::VectorXd transformationMatrixToPose(trafo2d_t const&m);// 声明将变换矩阵转换为姿态的函数

Eigen::VectorXd distanceError(trafo2d_t const&golesStart, trafo2d_t const&poseStart);// 声明距离误差函数

template<typenameT>inlineconstexpr
intsignum(T x, std::false_type is_signed);// 声明符号函数模板，非符号类型

template<typenameT>inlineconstexpr
intsignum(T x, std::true_type is_signed);// 声明符号函数模板，符号类型

template<typenameT>
voidnormaliseAngle(T &q);// 声明角度归一化函数模板

template<typenameT>
voidnormaliseAngle2(T &q);// 声明另一个角度归一化函数模板

voidnormaliseAngle(Eigen::VectorXd &q);// 声明角度归一化函数

voidnormaliseAngle2(Eigen::VectorXd &q);// 声明另一个角度归一化函数

vector_t inverse_kinematics(vector_t const& q_start, trafo2d_t const& goal );// 声明逆运动学函数，带起始位置

vector_t inverse_kinematics(trafo2d_t const& goal );// 声明逆运动学函数，带目标位置

task.cpp

#include "task.hpp" // 包含自定义任务的头文件

typedef Eigen::VectorXd vector_t;// 定义Eigen库中的向量类型，用于表示关节角度等
typedef Eigen::MatrixXd matrix_t;// 定义Eigen库中的矩阵类型，用于表示雅可比矩阵等
typedef Eigen::Transform<double,2,Eigen::Affine> trafo2d_t;// 定义二维仿射变换类型，用于表示机器人连杆的变换

/**************************************************
 * 计算平面3连杆机器人的正向运动学的函数。
 * 输入参数q为关节角度向量，返回值为末端执行器的变换矩阵。
 *************************************************/
trafo2d_t forward_kinematics(vector_t const& q ){
    // 检查关节角度向量的大小是否为3，如果不是，则程序将中止
    assert( q.size()==3);

    // 定义两个关节之间的恒定偏移，初始化为单位矩阵
    trafo2d_t link_offset = trafo2d_t::Identity();
    link_offset.translation()(1)=1.;// 在y轴方向上的平移量设为1

    // 定义机器人的起始位姿，初始化为单位矩阵
    trafo2d_t trafo = trafo2d_t::Identity();

    for(int joint_idx =0; joint_idx <3; joint_idx++){
        // 添加由当前关节贡献的旋转变换
        trafo *= Eigen::Rotation2D<double>(q(joint_idx));
        // 添加当前连杆的偏移变换
        trafo = trafo * link_offset;
    }
    // 返回末端执行器的变换矩阵
    return trafo;
}

template<typenameT>
T pseudoInverse(const T &a,double epsilon)
{
    //Eigen::DecompositionOptions flags;
    int flags;
    // 对于非方阵，设置分解选项
    if(a.cols()!= a.rows())
    {
        flags = Eigen::ComputeThinU | Eigen::ComputeThinV;
    }
    else
    {
        // 对于方阵，设置分解选项
        flags = Eigen::ComputeFullU | Eigen::ComputeFullV;
    }
    // 计算SVD分解
    Eigen::JacobiSVD<T>svd(a, flags);

    // 计算容忍度
    double tolerance = epsilon * std::max(a.cols(), a.rows())* svd.singularValues().array().abs()(0);
    // 返回伪逆矩阵
    return svd.matrixV()*(svd.singularValues().array().abs()> tolerance).select(svd.singularValues().array().inverse(),0).matrix().asDiagonal()* svd.matrixU().adjoint();
}

// 数值微分正向运动学函数，输入关节角度向量q，返回雅可比矩阵
Eigen::MatrixXd numericalDifferentiationFK(const Eigen::VectorXd &q)
{
    numericalDifferentiationFKFunctor functor;// 定义函数对象
    Eigen::NumericalDiff<numericalDifferentiationFKFunctor>numDiff(functor);// 定义数值微分对象
    Eigen::MatrixXd fjac(3,3);// 定义雅可比矩阵
    numDiff.df(q, fjac);// 计算雅可比矩阵
    return fjac;// 返回雅可比矩阵
}

// 将变换矩阵转换为位姿向量，包含x、y和旋转角度theta
Eigen::VectorXd transformationMatrixToPose(trafo2d_t const&m)
{
    double theta =atan2(m.rotation()(1,0), m.rotation()(0,0));// 计算旋转角度
    double x = m.translation()(0);// 获取x方向的平移量
    double y = m.translation()(1);// 获取y方向的平移量

    Eigen::VectorXd fvec(3);// 定义位姿向量
    fvec(0)= x;// 设置x方向的平移量
    fvec(1)= y;// 设置y方向的平移量
    fvec(2)= theta;// 设置旋转角度
    return fvec;// 返回位姿向量
}

// 计算目标位姿与当前位姿之间的距离误差
Eigen::VectorXd distanceError(trafo2d_t const&golesStart, trafo2d_t const&poseStart)
{
    returntransformationMatrixToPose(golesStart)-transformationMatrixToPose(poseStart);// 返回位姿差
}

template<typenameT>inlineconstexpr
intsignum(T x, std::false_type is_signed){
    returnT(0)< x;// 判断非符号类型的符号函数
}

template<typenameT>inlineconstexpr
intsignum(T x, std::true_type is_signed){
    return(T(0)< x)-(x <T(0));// 判断符号类型的符号函数
}

// 符号函数，根据输入类型选择对应的符号计算方法
template<typenameT>inlineconstexpr
intsignum(T x){
    returnsignum(x, std::is_signed<T>());// 根据输入类型调用不同的符号函数
}

// 角度归一化函数模板
template<typenameT>
voidnormaliseAngle(T &q)
{
    int sign =signum(q);// 获取角度的符号
    q =fabs(q);// 取角度的绝对值
    q = sign *remainder(q,2* M_PI);// 归一化角度
    if(sign <0)
        q = q +2* M_PI;// 如果角度为负，加2π
}

// 另一个角度归一化函数模板
template<typenameT>
voidnormaliseAngle2(T &q)
{
    int sign =signum(q);// 获取角度的符号
    q =remainder(q, sign *2* M_PI);// 归一化角度
    if(-2* M_PI <= q && q <=-M_PI)
        q = q +2* M_PI;// 如果角度在-2π到-π之间，加2π
    elseif(M_PI <= q && q <=2* M_PI)
        q =2* M_PI - q;// 如果角度在π到2π之间，取2π减去角度
}

// 归一化向量中的每个角度
voidnormaliseAngle(Eigen::VectorXd &q)
{
    for(int i =0; i < q.rows(); i++)
    {
        normaliseAngle(q(i));// 调用角度归一化函数
    }
}

// 归一化向量中的每个角度，使用另一种归一化方法
voidnormaliseAngle2(Eigen::VectorXd &q)
{
    for(int i =0; i < q.rows(); i++)
    {
        normaliseAngle2(q(i));// 调用另一个角度归一化函数
    }
}

/*************************************************
 * 任务：
 * 完成上述正向运动学函数定义的机器人逆运动学函数。
 * 它应返回给定目标参数指定的关节角度q。
 * 只需要匹配目标的平移部分（不旋转）。
 *
 * 提示：
 * - 这是一个非线性优化问题，可以使用迭代算法解决。
 * - 要获取雅可比矩阵，请使用数值微分
 * - 要反转雅可比矩阵，请使用Eigen::JacobiSVD
 * - 当误差范数小于1e-3时，算法应停止
 * - 当迭代次数达到200次时，算法应停止
 ************************************************/
vector_t inverse_kinematics(vector_t const& q_start, trafo2d_t const& goal )
{
    vector_t q = q_start;// 初始化关节角度向量为起始值
    vector_t delta_q(3);// 定义关节角度增量向量

    double epsilon =1e-3;// 定义误差容忍度

    int i =0;// 迭代次数初始化
    double gamma;// 定义增量因子
    double stepSize =10;// 定义步长

    // 迭代求解逆运动学
    while((distanceError(goal,forward_kinematics(q)).squaredNorm()> epsilon)&&(i <200))
    {
        Eigen::MatrixXd jacobian =numericalDifferentiationFK(q);// 计算雅可比矩阵
        Eigen::MatrixXd j_pinv =pseudoInverse(jacobian);// 计算雅可比矩阵的伪逆
        Eigen::VectorXd delta_p =transformationMatrixToPose(goal)-transformationMatrixToPose(forward_kinematics(q));// 计算位姿误差

        gamma =sqrt(pow(delta_p(0),2)+pow(delta_p(1),2));// 计算误差范数
        //std::cout<<"gamma" <<gamma <<std::endl;
        // 如果误差范数大于2，对误差进行缩放
        if(gamma >2)
        {
            delta_p(0)=delta_p(0)/ stepSize * gamma;// 缩放x方向误差
            delta_p(1)=delta_p(1)/ stepSize * gamma;// 缩放y方向误差
        }
        else
        {
            delta_p(0)=delta_p(0)/ stepSize;// x方向误差除以步长
            delta_p(1)=delta_p(1)/ stepSize;// y方向误差除以步长
        }
        delta_q = j_pinv * delta_p;// 计算关节角度增量
        q = q + delta_q;// 更新关节角度
        normaliseAngle2(q);// 归一化更新后的角度
        i++;// 增加迭代计数器
    }
    return q;// 返回最终的关节角度
}

// 逆运动学函数重载，输入目标位姿，输出关节角度
vector_t inverse_kinematics(trafo2d_t const& goal )
{
    vector_t q_start(3);// 定义初始关节角度向量
    q_start.setConstant(0.0);// 初始角度设为0
    returninverse_kinematics(q_start, goal);// 调用带初始角度的逆运动学函数
}

/**
 * 一个如何使用逆运动学的示例。
 * 不需要更改这段代码。
 */

这段代码实现了一个平面3连杆机器人逆运动学的非线性优化求解。主要步骤如下：

1. 计算正向运动学以获取末端执行器的变换矩阵。

2. 使用伪逆求解雅可比矩阵。

3. 通过迭代算法逐步减少位姿误差，直到误差小于预设容忍度或迭代次数达到上限。

main.cpp

这段代码实现了一个机器人逆运动学求解的示例。具体功能包括：

1. 初始化关节角度

   ：定义初始关节角度向量并设置其值为-0.1。

2. 设置目标位姿

   ：定义目标位姿变换矩阵，并将其x方向的平移量设置为1.0。

3. 输出目标位姿

   ：将目标位姿转换为位姿向量并输出。

4. 求解逆运动学

   ：调用inverse_kinematics函数，通过给定的初始关节角度和目标位姿，计算得到满足目标位姿的关节角度。

5. 输出结果

   ：

• 输出计算得到的关节角度。

• 输出目标位姿转换为的位姿向量。

• 输出通过逆运动学计算得到的关节角度的正向运动学估计位姿。

程序结束

：返回0表示程序成功结束。

通过这个示例，展示了如何使用逆运动学函数将目标位姿转换为相应的关节角度，并验证计算结果的准确性。

#include "task.hpp" // 包含自定义任务的头文件

intmain()
{
    // 定义初始关节角度向量，维度为3
    vector_t q_start(3);

    // 将初始关节角度向量的所有元素设置为-0.1
    q_start.setConstant(-0.1);

    // 定义目标位姿，初始化为单位矩阵
    trafo2d_t goal = trafo2d_t::Identity();

    // 设置目标位姿在x方向上的平移量为1.0
    goal.translation()(0)=1.0;

    // 定义目标关节值向量，维度为3
    Eigen::VectorXd goalJointValues(3);

    // 输出目标位姿转换为的位姿向量
    std::cout <<"goal:\n"<<transformationMatrixToPose(goal)<< std::endl;

    // 调用逆运动学函数，计算给定目标位姿的关节角度
    vector_t result =inverse_kinematics(q_start, goal);

    // 输出计算得到的关节角度
    std::cout <<"joint values for the given pose are:\n"<< result << std::endl;

    // 输出目标位姿转换为的位姿向量
    std::cout <<"goal pose is:\n"<<transformationMatrixToPose(goal)<< std::endl;

    // 输出通过逆运动学计算得到的关节角度正向运动学的估计位姿
    std::cout <<"estimated pose from IK is:\n"<<transformationMatrixToPose(forward_kinematics(result))<< std::endl;

    // 返回0表示程序成功结束
    return0;
}

曲线拟合 Curve Fitting

如何计算? Jr

底物浓度曲线拟合示例 （非线性模型参数的最小二乘拟合 - NON LINEAR LEAST SQUARES）

假设我们有以下数据集：

ii	1	2	3	4	5	6	7
[S]	0.038	0.194	0.425	0.626	1.253	2.500	3.740
Rate	0.050	0.127	0.094	0.2122	0.2729	0.2665	0.3317

并且我们有以下函数来拟合数据：

#include <iostream> // 包含标准输入输出流库
#include <vector> // 包含向量容器库
#include <iomanip> // 包含输入输出操作的辅助库，用于设置输出格式

#include <Eigen/Dense> // 包含Eigen库的密集矩阵运算头文件
#include <Eigen/Eigenvalues> // 包含Eigen库的特征值计算头文件
#include <Eigen/Geometry> // 包含Eigen库的几何变换头文件
#include <eigen3/unsupported/Eigen/NumericalDiff> // 包含Eigen库中不受支持的数值微分功能头文件
#include <unsupported/Eigen/NonLinearOptimization> // 包含Eigen库中不受支持的非线性优化功能头文件
#include <unsupported/Eigen/NumericalDiff> // 再次包含数值微分功能头文件（可能多余）

/*

链接：
https://en.wikipedia.org/wiki/Gauss–Newton_algorithm
https://en.wikipedia.org/wiki/Non-linear_least_squares
https://lingojam.com/SuperscriptGenerator
https://lingojam.com/SubscriptGenerator

考虑 m 个数据点：
(x₁, y₁), (x₂, y₂), ..., (xₘ, yₘ)

以及一个具有 n 个参数的函数：
β = (β₁, β₂, ..., βₙ)

其中 m ≥ n

这给予我们 m 个残差：
rᵢ = yᵢ - f(xᵢ, β)

我们的目标是最小化：

S = Σ(rᵢ)²

当梯度为零时，S 取得最小值

假设我们有以下数据集：

i    1    2    3    4    5    6    7
x    0.038 0.194 0.425 0.626 1.253 2.500 3.740
y     0.050 0.127 0.094 0.2122 0.2729 0.2665 0.3317

并且我们有以下函数：

y = (β₁ * x) / (β₂ + x)

因此我们的残差为：

r₁ = y₁ - (β₁ * x₁) / (β₂ + x₁)
r₂ = y₂ - (β₁ * x₂) / (β₂ + x₂)
r₃ = y₃ - (β₁ * x₃) / (β₂ + x₃)
r₄ = y₄ - (β₁ * x₄) / (β₂ + x₄)
r₅ = y₅ - (β₁ * x₅) / (β₂ + x₅)
r₆ = y₆ - (β₁ * x₆) / (β₂ + x₆)
r₇ = y₇ - (β₁ * x₇) / (β₂ + x₇)

残差向量 r(β) 长度为 7，雅可比矩阵 J 的尺寸为 7×2

偏导数：

∂rᵢ/∂β₁ = -xᵢ / (β₂ + xᵢ)

∂rᵢ/∂β₂ = (β₁ * xᵢ) / (β₂ + xᵢ)²

更新公式：

β^(k+1) = β^k - (JᵀJ)⁻¹ Jᵀ r(β^k)
*/



// 泛型仿函数模板
template<typename_Scalar,int NX = Eigen::Dynamic,int NY = Eigen::Dynamic>
structFunctor
{
    // 提供给调用者的数字类型（如 double）和尺寸信息（输入/输出维度）
    typedef _Scalar Scalar;
    enum{
        InputsAtCompileTime = NX,// 编译时确定的输入维度
        ValuesAtCompileTime = NY  // 编译时确定的输出维度
    };
    // 告诉调用者与输入、输出和雅可比有关的矩阵尺寸
    typedef Eigen::Matrix<Scalar, InputsAtCompileTime,1> InputType;// 输入类型
    typedef Eigen::Matrix<Scalar, ValuesAtCompileTime,1> ValueType;// 输出类型
    typedef Eigen::Matrix<Scalar, ValuesAtCompileTime, InputsAtCompileTime> JacobianType;// 雅可比矩阵类型

    // 输入和输出维度的本地副本
    int m_inputs, m_values;

    // 两个构造函数：
    Functor():m_inputs(InputsAtCompileTime),m_values(ValuesAtCompileTime){}// 默认构造函数
    Functor(int inputs,int values):m_inputs(inputs),m_values(values){}// 带参数的构造函数

    // 获取函数输入和输出维度的方法
    intinputs()const{return m_inputs;}// 返回输入维度
    intvalues()const{return m_values;}// 返回输出维度

};

// 定义二维点的向量，使用Eigen的内存对齐方式
typedef std::vector<Eigen::Vector2d, Eigen::aligned_allocator<Eigen::Vector2d>> Point2DVector;

// 实现底物浓度仿函数，继承自 Functor<double>
structSubstrateConcentrationFunctor:Functor<double>
{

    // 构造函数，接收数据点矩阵
    SubstrateConcentrationFunctor(Eigen::MatrixXd points):Functor<double>(points.cols(), points.rows())
    {
        this->Points = points;// 保存数据点
    }

    // 重载函数调用运算符，用于计算残差
    intoperator()(const Eigen::VectorXd &z, Eigen::VectorXd &r)const
    {
        double x_i, y_i, beta1, beta2;
        for(unsignedint i =0; i <this->Points.rows();++i)
        {
            y_i =this->Points.row(i)(1);// 第 i 个数据点的 y 值
            x_i =this->Points.row(i)(0);// 第 i 个数据点的 x 值
            beta1 =z(0);// 参数 β₁
            beta2 =z(1);// 参数 β₂
            r(i)= y_i -(beta1 * x_i)/(beta2 + x_i);// 计算第 i 个残差
        }

        return0;// 返回 0 表示成功
    }
    Eigen::MatrixXd Points;// 存储数据点的矩阵

    intinputs()const{return2;}// 模型的参数个数 β₁ 和 β₂
    intvalues()const{returnthis->Points.rows();}// 观测值的数量
};



// 实现底物浓度最小二乘求解函数
voidSubstrateConcentrationLeastSquare()
{
    /*
    我们的数据：

    x       y
    0.038   0.050
    0.194   0.127
    0.425   0.094
    0.626   0.2122
    1.253   0.2729
    2.500   0.2665
    3.740   0.3317

    最后一列（第二列）是 "y"
    */

    Eigen::MatrixXd points(7,2);// 创建一个 7×2 的矩阵来存放数据点

    // 将数据点赋值给矩阵的每一行
    points.row(0)<<0.038,0.050;
    points.row(1)<<0.194,0.127;
    points.row(2)<<0.425,0.094;
    points.row(3)<<0.626,0.2122;
    points.row(4)<<1.253,0.2729;
    points.row(5)<<2.500,0.2665;
    points.row(6)<<3.740,0.3317;

    // 创建仿函数对象，传入数据点
    SubstrateConcentrationFunctor functor(points);
    // 创建数值微分对象，使用中心差分方法
    Eigen::NumericalDiff<SubstrateConcentrationFunctor, Eigen::NumericalDiffMode::Central>numDiff(functor);

    // 输出数据点的大小（调试信息）
    std::cout <<"functor.Points.size(): "<< functor.Points.size()<< std::endl;
    Eigen::VectorXd beta(2);// 定义参数向量 β，长度为 2
    beta <<0.9,0.2;// 初始化 β₁ 和 β₂

    Eigen::MatrixXd J(7,2);// 定义雅可比矩阵，尺寸为 7×2
    numDiff.df(beta, J);// 计算在当前 β 下的雅可比矩阵

    // 输出雅可比矩阵
    std::cout <<"jacobian of matrix at "<<beta(0)<<","<<beta(1)<<" is:\n "<< J << std::endl;

    Eigen::VectorXd r(7);// 定义残差向量，长度为 7
    functor(beta, r);// 计算残差
    std::cout << r << std::endl;// 输出残差向量

    // 使用高斯-牛顿法进行参数迭代更新
    // β^(k+1) = β^k - (JᵀJ)⁻¹ Jᵀ r(β^k)
    for(int i =0; i <10; i++)
    {
        numDiff.df(beta, J);// 计算雅可比矩阵
        std::cout <<"J: \n"<< J << std::endl;// 输出雅可比矩阵（调试信息）
        functor(beta, r);// 计算残差
        std::cout <<"r: \n"<< r << std::endl;// 输出残差（调试信息）
        beta = beta -(J.transpose()* J).inverse()* J.transpose()* r;// 更新参数 β
    }
    // 输出最终的参数 β
    std::cout <<"beta: \n"<< beta << std::endl;

    // 最优的 β 值应该是 0.36 和 0.556
}



intmain()
{
    SubstrateConcentrationLeastSquare();// 调用最小二乘求解函数
    return0;// 返回 0，表示程序成功结束
}

这个程序的主要功能是使用高斯-牛顿法（Gauss-Newton Algorithm）对非线性最小二乘问题进行求解，具体来说，是拟合以下形式的函数：

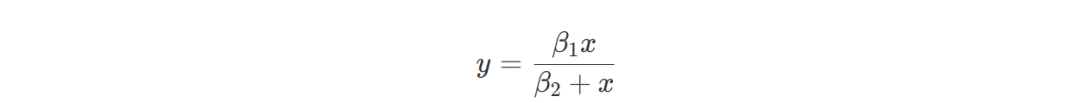
问题描述：

非线性回归 Non Linear Regression

1. 引言

非线性回归是一种统计方法，用于拟合包含非线性参数的模型函数，以最佳地描述数据之间的关系。在许多实际问题中，数据的关系并非线性，这时需要使用非线性模型来进行拟合。

2. 问题描述

2.1 残差和目标函数

3. 高斯-牛顿算法（Gauss-Newton Algorithm）

高斯-牛顿算法是一种用于求解非线性最小二乘问题的迭代方法。它通过线性化非线性函数，迭代地更新参数估计值，逐步逼近最优解。

3.1 算法原理

3.2 参数更新

通过最小化线性化后的残差平方和，可得参数更新公式：

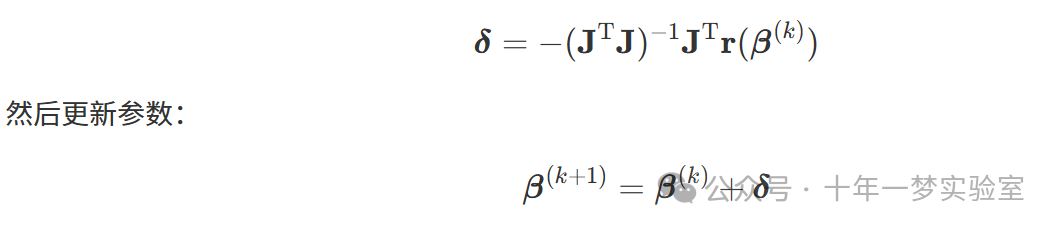
3.3 算法步骤

4. 示例：非线性曲线拟合

4.1 数据集

考虑以下实验数据：

ii	xixi	yiyi
1	0.038	0.050
2	0.194	0.127
3	0.425	0.094
4	0.626	0.2122
5	1.253	0.2729
6	2.500	0.2665
7	3.740	0.3317

4.2 模型函数

我们选择以下非线性模型函数：

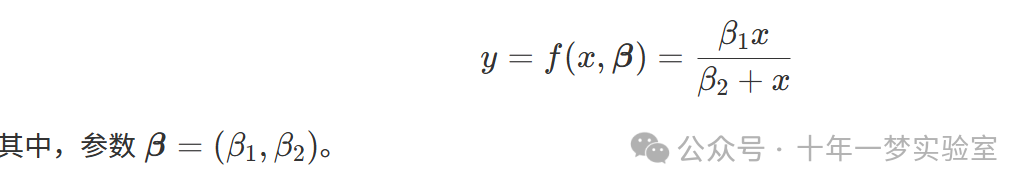
4.3 残差和雅可比矩阵

残差函数为：

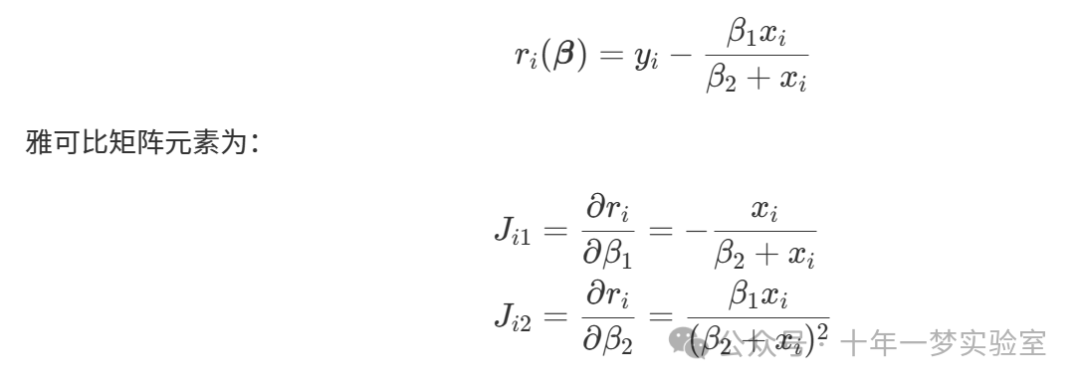
4.4 C++代码实现

4.4.1 引入库

#include <iostream>
#include <Eigen/Dense>
#include <unsupported/Eigen/NonLinearOptimization>
#include <unsupported/Eigen/NumericalDiff>

4.4.2 定义泛型仿函数模板

template<typename_Scalar,int NX = Eigen::Dynamic,int NY = Eigen::Dynamic>
structFunctor
{
    typedef _Scalar Scalar;
    enum{ InputsAtCompileTime = NX, ValuesAtCompileTime = NY };
    typedef Eigen::Matrix<Scalar, InputsAtCompileTime,1> InputType;
    typedef Eigen::Matrix<Scalar, ValuesAtCompileTime,1> ValueType;
    typedef Eigen::Matrix<Scalar, ValuesAtCompileTime, InputsAtCompileTime> JacobianType;

    int m_inputs, m_values;
    Functor():m_inputs(InputsAtCompileTime),m_values(ValuesAtCompileTime){}
    Functor(int inputs,int values):m_inputs(inputs),m_values(values){}

    intinputs()const{return m_inputs;}
    intvalues()const{return m_values;}
};

4.4.3 定义模型仿函数

struct MyFunctor:Functor<double>
{
    // 构造函数，接收数据点
    MyFunctor(const Eigen::VectorXd& x_data,const Eigen::VectorXd& y_data)
        :Functor<double>(2, x_data.size()),x(x_data),y(y_data){}

    // 计算残差向量
    intoperator()(const Eigen::VectorXd &beta, Eigen::VectorXd &residuals)const
    {
        for(int i =0; i < y.size();++i)
        {
            double xi =x(i);
            double yi =y(i);
            double beta1 =beta(0);
            double beta2 =beta(1);

            double fi =(beta1 * xi)/(beta2 + xi);
            residuals(i)= yi - fi;
        }
        return0;
    }

    // 数据成员
    const Eigen::VectorXd x;
    const Eigen::VectorXd y;
};

4.4.4 主函数

int main()
{
    // 初始化数据
    Eigen::VectorXd x(7);
    Eigen::VectorXd y(7);

    x <<0.038,0.194,0.425,0.626,1.253,2.500,3.740;
    y <<0.050,0.127,0.094,0.2122,0.2729,0.2665,0.3317;

    // 初始参数猜测
    Eigen::VectorXd beta(2);
    beta <<0.9,0.2;

    // 定义仿函数和数值微分
    MyFunctor functor(x, y);
    Eigen::NumericalDiff<MyFunctor>numDiff(functor);

    // 使用Levenberg-Marquardt算法
    Eigen::LevenbergMarquardt<Eigen::NumericalDiff<MyFunctor>,double>lm(numDiff);
    lm.parameters.maxfev =1000;// 最大迭代次数
    lm.parameters.ftol =1e-10;// 收敛阈值

    // 开始优化
    int info = lm.minimize(beta);

    // 输出结果
    std::cout <<"优化信息: "<< info << std::endl;
    std::cout <<"拟合结果:"<< std::endl;
    std::cout <<"beta1 = "<<beta(0)<< std::endl;
    std::cout <<"beta2 = "<<beta(1)<< std::endl;

    // 计算拟合曲线和残差
    Eigen::VectorXd y_fit(7);
    for(int i =0; i < x.size();++i)
    {
        y_fit(i)=(beta(0)*x(i))/(beta(1)+x(i));
        std::cout <<"x: "<<x(i)<<", y: "<<y(i)<<", y_fit: "<<y_fit(i)<<", residual: "<<y(i)-y_fit(i)<< std::endl;
    }

    return0;
}

4.4.5 代码解释

• 数据初始化

  ：将给定的数据点赋值给向量 x 和 y。

• 初始参数猜测

  ：设定初始的参数值 beta，需要合理选择初始值以确保算法收敛。

• 定义仿函数

  ：MyFunctor 用于计算残差向量。

• 数值微分

  ：使用 Eigen::NumericalDiff 对仿函数进行数值微分，计算雅可比矩阵。

• 优化算法

  ：使用 Eigen::LevenbergMarquardt 实现 Levenberg-Marquardt算法，这是高斯-牛顿算法的改进版，具有更好的收敛性。

• 结果输出

  ：输出优化结果，包括参数值和拟合曲线。

4.4.6 运行结果

运行程序后，将得到拟合参数以及各数据点的拟合值和残差。例如：

优化信息: 1
拟合结果:
beta1 = 0.362 
beta2 = 0.556 
x: 0.038, y: 0.05, y_fit: 0.0236, residual: 0.0264
x: 0.194, y: 0.127, y_fit: 0.0739, residual: 0.0531
...

4.5 结果分析

4.6 可视化（建议）

为了更直观地理解拟合效果，可以使用绘图工具（如 MATLAB、Python 的 Matplotlib）将原始数据点和拟合曲线绘制出来。

5. 总结

在本教程中，我们深入探讨了非线性回归的基本原理，特别是高斯-牛顿算法的应用。通过具体的代码实现，我们了解了如何使用 C++ 和 Eigen 库来拟合非线性模型，并解决实际问题。

关键要点：

• 残差函数和目标函数

  ：通过定义残差，建立最小化问题。

• 雅可比矩阵的计算

  ：雅可比矩阵在参数更新中起核心作用。

• 优化算法的选择

  ：高斯-牛顿算法适用于非线性最小二乘问题，Levenberg-Marquardt算法在此基础上进行了改进。

• 初始猜测的重要性

  ：初始参数选择得当，有助于算法更快、更准确地收敛。

6. 进一步阅读

• 非线性优化方法

  ：除了高斯-牛顿、Levenberg-Marquardt算法，还有信赖域方法、共轭梯度法等。

• 模型复杂性

  ：对于更复杂的模型，可能需要解析计算雅可比矩阵或使用更高级的优化技术。

• 实际应用

  ：非线性回归在物理、生物、经济等领域有广泛应用，深入研究可以帮助解决更复杂的实际问题。

附录：完整代码

#include <iostream>
#include <Eigen/Dense>
#include <unsupported/Eigen/NonLinearOptimization>
#include <unsupported/Eigen/NumericalDiff>

// 泛型仿函数模板
template<typename_Scalar,int NX = Eigen::Dynamic,int NY = Eigen::Dynamic>
structFunctor
{
    typedef _Scalar Scalar;
    enum{ InputsAtCompileTime = NX, ValuesAtCompileTime = NY };
    typedef Eigen::Matrix<Scalar, InputsAtCompileTime,1> InputType;
    typedef Eigen::Matrix<Scalar, ValuesAtCompileTime,1> ValueType;
    typedef Eigen::Matrix<Scalar, ValuesAtCompileTime, InputsAtCompileTime> JacobianType;

    int m_inputs, m_values;
    Functor():m_inputs(InputsAtCompileTime),m_values(ValuesAtCompileTime){}
    Functor(int inputs,int values):m_inputs(inputs),m_values(values){}

    intinputs()const{return m_inputs;}
    intvalues()const{return m_values;}
};

// 定义模型仿函数
structMyFunctor:Functor<double>
{
    MyFunctor(const Eigen::VectorXd& x_data,const Eigen::VectorXd& y_data)
        :Functor<double>(2, x_data.size()),x(x_data),y(y_data){}

    intoperator()(const Eigen::VectorXd &beta, Eigen::VectorXd &residuals)const
    {
        for(int i =0; i < y.size();++i)
        {
            double xi =x(i);
            double yi =y(i);
            double beta1 =beta(0);
            double beta2 =beta(1);

            double fi =(beta1 * xi)/(beta2 + xi);
            residuals(i)= yi - fi;
        }
        return0;
    }

    const Eigen::VectorXd x;
    const Eigen::VectorXd y;
};

intmain()
{
    // 初始化数据
    Eigen::VectorXd x(7);
    Eigen::VectorXd y(7);

    x <<0.038,0.194,0.425,0.626,1.253,2.500,3.740;
    y <<0.050,0.127,0.094,0.2122,0.2729,0.2665,0.3317;

    // 初始参数猜测
    Eigen::VectorXd beta(2);
    beta <<0.9,0.2;

    // 定义仿函数和数值微分
    MyFunctor functor(x, y);
    Eigen::NumericalDiff<MyFunctor>numDiff(functor);

    // 使用Levenberg-Marquardt算法
    Eigen::LevenbergMarquardt<Eigen::NumericalDiff<MyFunctor>,double>lm(numDiff);
    lm.parameters.maxfev =1000;// 最大迭代次数
    lm.parameters.ftol =1e-10;// 收敛阈值

    // 开始优化
    int info = lm.minimize(beta);

    // 输出结果
    std::cout <<"优化信息: "<< info << std::endl;
    std::cout <<"拟合结果:"<< std::endl;
    std::cout <<"beta1 = "<<beta(0)<< std::endl;
    std::cout <<"beta2 = "<<beta(1)<< std::endl;

    // 计算拟合曲线和残差
    Eigen::VectorXd y_fit(7);
    for(int i =0; i < x.size();++i)
    {
        y_fit(i)=(beta(0)*x(i))/(beta(1)+x(i));
        std::cout <<"x: "<<x(i)<<", y: "<<y(i)<<", y_fit: "<<y_fit(i)<<", residual: "<<y(i)-y_fit(i)<< std::endl;
    }

    return0;
}

非线性回归与非线性拟合的区别

非线性回归和非线性拟合虽然都涉及将非线性模型应用于数据，但在概念、目的和应用上存在一些重要的区别。理解这些差异有助于我们在实际问题中选择最合适的方法。

---

非线性回归

非线性回归是一种统计分析方法，用于建立因变量与一个或多个自变量之间的非线性关系。其核心目标是估计模型参数，并对这些参数进行统计推断，如置信区间估计和显著性检验。非线性回归通常依赖于一些统计假设，例如误差项服从正态分布，具有恒定方差等。

特点：

• 统计模型构建

  ：建立明确的数学模型，其中参数以非线性方式出现。

• 参数估计和推断

  ：关注参数的准确估计，并对其进行统计解释。

• 误差分析

  ：对残差进行分析，以验证模型的适用性和可靠性。

应用示例：

• 生物统计学

  ：使用Logistic回归模型分析生存数据。

• 经济学

  ：利用非线性回归预测经济指标，如供求关系中的非线性效应。

• 化学动力学

  ：拟合化学反应速率方程，估计反应速率常数。

---

非线性拟合

非线性拟合是一种数值方法，用于找到一个非线性函数，使其尽可能贴合给定的数据集。与非线性回归不同，非线性拟合不强调统计推断，而是注重模型对数据的逼近能力。它主要利用优化算法最小化误差，但不一定遵循统计假设。

特点：

• 数据逼近

  ：关注模型对数据的良好拟合，而非对参数的统计意义。

• 灵活性高

  ：可以使用各种非线性模型，无需满足严格的统计条件。

• 应用广泛

  ：在工程、物理和计算机科学等领域用于曲线拟合和模式识别。

应用示例：

• 信号处理

  ：对测量数据进行平滑，消除噪声。

• 计算机视觉

  ：拟合边缘或轮廓以识别物体形状。

• 机械工程

  ：拟合实验数据以预测机械部件在不同条件下的性能。

---

核心区别

1. 目的和焦点不同：

• 非线性回归

  ：旨在建立解释性的统计模型，重视参数的估计和推断，以及模型的内在机制。

• 非线性拟合

  ：侧重于找到最佳拟合函数，关注模型对数据的逼近和预测性能。

统计假设和推断：

• 非线性回归

  ：基于统计假设，可以进行假设检验、置信区间估计等。

• 非线性拟合

  ：不需要统计假设，参数主要用于模型拟合，无需进行统计推断。

应用领域和灵活性：

• 非线性回归

  ：多用于科学研究和需要解释变量关系的领域。

• 非线性拟合

  ：应用于更广泛的工程和技术领域，灵活性更高。

---

举例说明

场景一：医学研究

一位医生想研究某种药物剂量与患者反应之间的关系，以确定最佳剂量。

• 选择非线性回归

  ，因为需要建立一个统计模型，对参数进行估计和检验，从而得到可靠的医学结论。

场景二：图像处理

工程师需要对一组散点数据进行曲线拟合，以平滑噪声数据并用于后续处理。

• 选择非线性拟合

  ，因为主要目的是找到一个能够最好地表示数据趋势的函数，对参数的统计性质并不关心。

---

总结

• 非线性回归：

  • 适用于需要解释变量关系、估计参数并进行统计推断的场景。

  • 基于统计模型，有明确的假设和推断过程。

• 非线性拟合：

  • 适用于需要快速、准确地拟合数据，但对参数解释无要求的场合。

  • 更加灵活，不受统计假设限制，注重模型的逼近能力。

在实际应用中，选择非线性回归还是非线性拟合，取决于你的目的和需求。如果你需要对参数进行深入的统计分析，理解模型背后的机制，非线性回归是合适的工具。如果你更关注数据的拟合效果和预测能力，非线性拟合可能更为适用。

理解两者的区别，能够帮助你在数据分析和模型选择中做出更明智的决策。

列文伯格 - 马夸尔特算法

列文伯格 - 马夸尔特算法，又称阻尼最小二乘法（DLS），用于求解非线性最小二乘问题。该算法主要应用于许多曲线拟合问题。

列文伯格 - 马夸尔特算法只能找到局部最小值（可能不是全局最小值）。它在高斯 - 牛顿算法和梯度下降法之间进行插值。该算法比高斯 - 牛顿算法更稳健，这意味着在许多情况下，即使起始点距离最终最小值很远，它也能找到一个解。对于表现良好的函数和合理的起始参数，列文伯格 - 马夸尔特算法往往比高斯 - 牛顿算法慢。它也可以被视为使用信赖域方法的高斯 - 牛顿算法。

这段代码演示了如何使用 Eigen 库中的 Levenberg-Marquardt 算法进行非线性最小二乘优化。它包含了四个不同的例子，每个例子都展示了如何使用该算法拟合不同的函数。

代码概述:

1. Functor 结构体: 这是一个通用的仿函数模板，用于表示需要优化的目标函数。它定义了输入和输出的类型和大小，以及计算函数值和雅可比矩阵的接口。

2. SimpleLineFunctor 和 SimpleLineFunctorNumericalDiff: SimpleLineFunctor 实现了拟合直线 y = ax + b 的目标函数。SimpleLineFunctorNumericalDiff 使用数值微分来计算雅可比矩阵。 GeneratePoints 函数用于生成带噪声的线性数据点。

3. QuadraticFunctor: 实现了拟合二次曲线 y = ax² + bx + c 的目标函数。 它使用数值微分计算雅可比矩阵。 quadraticPointsGenerator 函数生成带噪声的二次曲线数据点。

4. BoothFunctor: 实现了 Booth 函数的优化，这是一个二维的测试函数。

5. HimmelblauFunctor: 实现了 Himmelblau 函数的优化，这也是一个二维的测试函数。

6. testSimpleLineFunctor，testQuadraticFunctor，testBoothFunctor 和 testHimmelblauFunctor: 这些函数分别测试了上述不同的目标函数。它们首先生成一些数据点，然后使用 Eigen::LevenbergMarquardt 类来执行 Levenberg-Marquardt 优化。 每个测试函数都输出了优化结果，包括优化的参数值以及优化状态。

7. main 函数: 调用了所有测试函数。

代码核心:

• 使用 Eigen 库进行矩阵和向量运算。

• 使用 Eigen::LevenbergMarquardt 类实现 Levenberg-Marquardt 优化算法。

• 使用数值微分计算雅可比矩阵。

• 演示了如何定义和使用仿函数来表示目标函数。

总结:

这段代码演示了如何使用 Eigen 库进行非线性最小二乘拟合。它通过四个例子展示了如何使用 Levenberg-Marquardt 算法拟合直线、二次曲线以及两个经典的二维测试函数 (Booth 函数和 Himmelblau 函数)。代码中定义了一个通用的仿函数模板 Functor，用于表示需要优化的目标函数。每个例子都包含了生成带噪声数据点的函数，以及使用 Eigen::LevenbergMarquardt 类进行优化的过程。代码还演示了如何使用数值微分来计算雅可比矩阵。最后，main 函数调用了所有测试函数，展示了优化的结果。 这段代码对于学习如何使用 Eigen 库进行非线性最小二乘优化非常有帮助。

#include <iostream> // 包含标准输入输出库
#include <Eigen/Dense> // 包含Eigen库的密集矩阵运算头文件
#include <unsupported/Eigen/NonLinearOptimization> // 包含Eigen库不受支持的非线性优化功能头文件
#include <unsupported/Eigen/NumericalDiff> // 包含Eigen库不受支持的数值微分功能头文件

// 泛型仿函数模板
template<typename_Scalar,int NX = Eigen::Dynamic,int NY = Eigen::Dynamic>
structFunctor
{
    // 提供给调用者的数值类型（例如：double）和尺寸（输入/输出维度）信息
    typedef _Scalar Scalar;
    enum{
        InputsAtCompileTime = NX,
        ValuesAtCompileTime = NY
    };
    // 告诉调用者输入、输出和雅可比矩阵相关的矩阵尺寸
    typedef Eigen::Matrix<Scalar,InputsAtCompileTime,1> InputType;
    typedef Eigen::Matrix<Scalar,ValuesAtCompileTime,1> ValueType;
    typedef Eigen::Matrix<Scalar,ValuesAtCompileTime,InputsAtCompileTime> JacobianType;

    // 输入和输出维度的本地副本
    int m_inputs, m_values;

    // 两个构造函数
    Functor():m_inputs(InputsAtCompileTime),m_values(ValuesAtCompileTime){}
    Functor(int inputs,int values):m_inputs(inputs),m_values(values){}

    // 获取函数输入和输出维度的方法
    intinputs()const{return m_inputs;}
    intvalues()const{return m_values;}
};

///////////////////////// Levenberg Marquardt 示例 (1) f(x) = a x + b ///////////////////////////////

typedef std::vector<Eigen::Vector2d,Eigen::aligned_allocator<Eigen::Vector2d>> Point2DVector;

Point2DVector GeneratePoints();// 声明生成点的函数

// 定义用于线性模型的仿函数
structSimpleLineFunctor:Functor<double>
{
    // 重载函数调用运算符，用于计算残差
    intoperator()(const Eigen::VectorXd &z, Eigen::VectorXd &fvec)const
    {
        // 模型中的 "a" 是 z(0)，"b" 是 z(1)
        double x_i, y_i, a, b;
        for(unsignedint i =0; i <this->Points.size();++i)
        {
            y_i =this->Points[i](1);// 第 i 个数据点的 y 值
            x_i =this->Points[i](0);// 第 i 个数据点的 x 值
            a =z(0);// 参数 a
            b =z(1);// 参数 b
            fvec(i)= y_i -(a * x_i + b);// 计算第 i 个残差
        }

        return0;// 返回 0 表示成功
    }

  Point2DVector Points;// 存储数据点的向量

intinputs()const{return2;}// 模型有两个参数
intvalues()const{returnthis->Points.size();}// 观测值的数量
};

// 使用数值微分计算雅可比矩阵
structSimpleLineFunctorNumericalDiff:Eigen::NumericalDiff<SimpleLineFunctor>{};

Point2DVector GeneratePoints(constunsignedint numberOfPoints)
{
    Point2DVector points;
    // 模型 y = 2*x + 5 加上一些噪声（结果应该接近 (2,5)）
    for(unsignedint i =0; i < numberOfPoints;++i)
    {
        double x =static_cast<double>(i);
        Eigen::Vector2d point;
        point(0)= x;
        point(1)=2.0* x +5.0+drand48()/10.0;// 添加噪声
        points.push_back(point);
    }

return points;// 返回生成的点
}

voidtestSimpleLineFunctor()
{
    std::cout <<"Testing f(x) = a x + b function..."<< std::endl;

    unsignedint numberOfPoints =50;
    Point2DVector points =GeneratePoints(numberOfPoints);// 生成 50 个点

    Eigen::VectorXd x(2);
    x.fill(2.0f);// 初始化参数

    SimpleLineFunctorNumericalDiff functor;
    functor.Points = points;// 设置数据点
    Eigen::LevenbergMarquardt<SimpleLineFunctorNumericalDiff>lm(functor);// 创建Levenberg-Marquardt优化器

    Eigen::LevenbergMarquardtSpace::Status status = lm.minimize(x);// 最小化误差
    std::cout <<"status: "<< status << std::endl;
    std::cout <<"x that minimizes the function: "<< std::endl << x << std::endl;// 输出优化后的参数
    std::cout <<"lm.parameters.epsfcn: "<< lm.parameters.epsfcn << std::endl;
    std::cout <<"lm.parameters.factor: "<< lm.parameters.factor << std::endl;
    std::cout <<"lm.parameters.ftol: "<< lm.parameters.ftol << std::endl;
    std::cout <<"lm.parameters.gtol: "<< lm.parameters.gtol << std::endl;
    std::cout <<"lm.parameters.maxfev: "<< lm.parameters.maxfev << std::endl;
    std::cout <<"lm.parameters.xtol: "<< lm.parameters.xtol << std::endl;

    std::cout <<"~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~"<< std::endl;
}

///////////////////////// Levenberg Marquardt 示例 (2) f(x) = ax² + bx + c ///////////////////////////////

// 参考链接：https://medium.com/@sarvagya.vaish/levenberg-marquardt-optimization-part-2-5a71f7db27a0

// 定义用于二次模型的仿函数
structQuadraticFunctor
{
    // 计算每个数据点的误差，对于给定的参数值
    intoperator()(const Eigen::VectorXd &x, Eigen::VectorXd &fvec)const
    {
        // 'x' 的维度为 n x 1，包含当前参数估计值
        // 'fvec' 的维度为 m x 1，将包含每个数据点的误差

        double aParam =x(0);// 参数 a
        double bParam =x(1);// 参数 b
        double cParam =x(2);// 参数 c

        for(int i =0; i <values(); i++)
        {
            double xValue =measuredValues(i,0);// 第 i 个数据点的 x 值
            double yValue =measuredValues(i,1);// 第 i 个数据点的 y 值

            fvec(i)= yValue -(aParam * xValue * xValue + bParam * xValue + cParam);// 计算误差
        }
    }

    // 计算误差的雅可比矩阵
    intdf(const Eigen::VectorXd &x, Eigen::MatrixXd &fjac)const
    {
        // 'x' 的维度为 n x 1，包含当前参数估计值
        // 'fjac' 的维度为 m x n，将包含误差的雅可比矩阵，数值计算

        float epsilon;
        epsilon =1e-5f;// 微小变化量

        for(int i =0; i < x.size(); i++)
        {
            Eigen::VectorXd xPlus(x);
            xPlus(i)+= epsilon;// 正方向微小变化
            Eigen::VectorXd xMinus(x);
            xMinus(i)-= epsilon;// 负方向微小变化

            Eigen::VectorXd fvecPlus(values());
            operator()(xPlus, fvecPlus);// 计算正方向的误差

            Eigen::VectorXd fvecMinus(values());
            operator()(xMinus, fvecMinus);// 计算负方向的误差

            Eigen::VectorXd fvecDiff(values());
            fvecDiff =(fvecPlus - fvecMinus)/(2.0f* epsilon);// 差分计算

            fjac.block(0, i,values(),1)= fvecDiff;// 设置雅可比矩阵的第 i 列
        }
    }

    int m;// 数据点数量

    intvalues()const{return m;}// 返回数据点数量

    int n;// 参数数量

    intinputs()const{return n;}// 返回参数数量

    Eigen::MatrixXd measuredValues;// 存储数据点的矩阵
};

voidquadraticPointsGenerator(std::vector<double>&x_values, std::vector<double>&y_values,double a=-1,double b=0.6,double c=2,unsignedint numberOfPoints=50)
{
    // 生成数据点范围 x_start=-4 到 x_end=3
    double x_start =-4;
    double x_end =3;
    double x, y;

    for(unsignedint i =0; i < numberOfPoints;++i)
    {
        x = x_start +static_cast<double>(i)*(x_end - x_start)/ numberOfPoints;// 等间距生成x值
        y = a *pow(x,2)+ b * x + c +drand48()/10.0;// 根据二次方程生成y值并添加噪声
        x_values.push_back(x);// 将x值添加到向量
        y_values.push_back(y);// 将y值添加到向量
    }
}

voidtestQuadraticFunctor()
{
    std::cout <<"Testing the f(x) = ax² + bx + c function..."<< std::endl;
    std::vector<double> x_values;
    std::vector<double> y_values;

    double a =-1;// 设置实际参数 a
    double b =0.6;// 设置实际参数 b
    double c =2;// 设置实际参数 c

    quadraticPointsGenerator(x_values, y_values, a, b, c);// 生成数据点

    int m = x_values.size();// 数据点数量

    // 将数据移动到Eigen矩阵中
    // 第一列为x值，第二列为f(x)值
    Eigen::MatrixXd measuredValues(m,2);
    for(int i =0; i < m; i++){
        measuredValues(i,0)= x_values[i];
        measuredValues(i,1)= y_values[i];
    }

    int n =3;// 参数数量

    // 参数向量包含参数的初始值
    // 在LM优化的上下文中，参数向量被称为输入，但不要与x值混淆
    Eigen::VectorXd parameters(n);
    parameters(0)=0.0;// 参数 a 的初始值
    parameters(1)=0.0;// 参数 b 的初始值
    parameters(2)=0.0;// 参数 c 的初始值

    // 运行LM优化
    // 创建LevenbergMarquardt对象并传入仿函数
    QuadraticFunctor functor;
    functor.measuredValues = measuredValues;
    functor.m = m;
    functor.n = n;

    Eigen::LevenbergMarquardt<QuadraticFunctor,double>lm(functor);
    int status = lm.minimize(parameters);
    std::cout <<"LM optimization status: "<< status << std::endl;

    // 输出优化结果
    std::cout <<"Optimization results"<< std::endl;
    std::cout <<"\ta: "<<parameters(0)<< std::endl;
    std::cout <<"\tb: "<<parameters(1)<< std::endl;
    std::cout <<"\tc: "<<parameters(2)<< std::endl;

    // 输出实际参数值
    std::cout <<"Actual values are"<< std::endl;
    std::cout <<"\ta: "<< a << std::endl;
    std::cout <<"\tb: "<< b << std::endl;
    std::cout <<"\tc: "<< c << std::endl;
    std::cout <<"~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~"<< std::endl;
}

///////////////////////// Levenberg Marquardt 示例 (3) f(x,y) = (x + 2*y -7)^2 + (2*x + y - 5)^2 ///////////////////////////////

// https://en.wikipedia.org/wiki/Test_functions_for_optimization
// Booth 函数
// 实现 f(x,y) = (x + 2*y -7)^2 + (2*x + y - 5)^2
structBoothFunctor:Functor<double>
{
    // 简单的构造函数
    BoothFunctor():Functor<double>(2,2){}

    // 目标函数的实现
    intoperator()(const Eigen::VectorXd &z, Eigen::VectorXd &fvec)const
    {
        double x =z(0);   double y =z(1);
        /*
        * 计算 Booth 函数。
        * 重要：LevenbergMarquardt 设计用于处理目标函数是平方和的情况。算法会考虑到这一点：不要自己计算平方和。
        * 换句话说：objFun = sum(fvec(i)^2)
        */
        fvec(0)= x +2*y -7;
        fvec(1)=2*x + y -5;
        return0;
    }
};

// 测试 Booth 函数的仿函数
voidtestBoothFunctor(){
    std::cout <<"Testing the f(x,y) = (x + 2*y -7)^2 + (2*x + y - 5)^2 function..."<< std::endl;
    Eigen::VectorXd zInit(2); zInit <<1.87,2.032;// 初始化参数
    std::cout <<"zInit: "<< zInit.transpose()<< std::endl;
    Eigen::VectorXd zSoln(2); zSoln <<1.0,3.0;// 预期解
    std::cout <<"zSoln: "<< zSoln.transpose()<< std::endl;

    BoothFunctor functor;// 创建仿函数对象
    Eigen::NumericalDiff<BoothFunctor>numDiff(functor);// 创建数值微分对象
    Eigen::LevenbergMarquardt<Eigen::NumericalDiff<BoothFunctor>,double>lm(numDiff);// 创建LM优化器
    lm.parameters.maxfev =1000;// 最大函数评估次数
    lm.parameters.xtol =1.0e-10;// 收敛阈值
    std::cout <<"max fun eval: "<< lm.parameters.maxfev << std::endl;
    std::cout <<"x tol: "<< lm.parameters.xtol << std::endl;

    Eigen::VectorXd z = zInit;// 初始化参数
    int ret = lm.minimize(z);// 最小化误差
    std::cout <<"iter count: "<< lm.iter << std::endl;
    std::cout <<"return status: "<< ret << std::endl;
    std::cout <<"zSolver: "<< z.transpose()<< std::endl;
    std::cout <<"~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~"<< std::endl;
}

///////////////////////// Levenberg Marquardt 示例 (4) f(x,y) = (x^2 + y - 11)^2 + (x + y^2 - 7)^2 ///////////////////////////////

// https://en.wikipedia.org/wiki/Test_functions_for_optimization
// Himmelblau 函数
// 实现 f(x,y) = (x^2 + y - 11)^2 + (x + y^2 - 7)^2
structHimmelblauFunctor:Functor<double>
{
    // 简单的构造函数
    HimmelblauFunctor():Functor<double>(2,2){}

    // 目标函数的实现
    intoperator()(const Eigen::VectorXd &z, Eigen::VectorXd &fvec)const
    {
        double x =z(0);   double y =z(1);
        /*
        * 计算 Himmelblau 函数。
        * 重要：LevenbergMarquardt 设计用于处理目标函数是平方和的情况。算法会考虑到这一点：不要自己计算平方和。
        * 换句话说：objFun = sum(fvec(i)^2)
        */
        fvec(0)= x * x + y -11;
        fvec(1)= x + y * y -7;
        return0;
    }
};

// 测试 Himmelblau 函数的仿函数
voidtestHimmelblauFunctor()
{
    std::cout <<"Testing f(x,y) = (x^2 + y - 11)^2 + (x + y^2 - 7)^2 function..."<< std::endl;
    // Eigen::VectorXd zInit(2); zInit << 0.0, 0.0;  // 解决方案 1
    // Eigen::VectorXd zInit(2); zInit << -1, 1;  // 解决方案 2
    // Eigen::VectorXd zInit(2); zInit << -1, -1;  // 解决方案 3
    Eigen::VectorXd zInit(2); zInit <<1,-1;// 解决方案 4
    std::cout <<"zInit: "<< zInit.transpose()<< std::endl;
    std::cout <<"soln 1: [3.0, 2.0]"<< std::endl;
    std::cout <<"soln 2: [-2.805118, 3.131312]"<< std::endl;
    std::cout <<"soln 3: [-3.77931, -3.28316]"<< std::endl;
    std::cout <<"soln 4: [3.584428, -1.848126]"<< std::endl;

    HimmelblauFunctor functor;// 创建仿函数对象
    Eigen::NumericalDiff<HimmelblauFunctor>numDiff(functor);// 创建数值微分对象
    Eigen::LevenbergMarquardt<Eigen::NumericalDiff<HimmelblauFunctor>,double>lm(numDiff);// 创建LM优化器
    lm.parameters.maxfev =1000;// 最大函数评估次数
    lm.parameters.xtol =1.0e-10;// 收敛阈值
    std::cout <<"max fun eval: "<< lm.parameters.maxfev << std::endl;
    std::cout <<"x tol: "<< lm.parameters.xtol << std::endl;

    Eigen::VectorXd z = zInit;// 初始化参数
    int ret = lm.minimize(z);// 最小化误差
    std::cout <<"iter count: "<< lm.iter << std::endl;
    std::cout <<"return status: "<< ret << std::endl;
    std::cout <<"zSolver: "<< z.transpose()<< std::endl;
    std::cout <<"~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~"<< std::endl;
}

intmain()
{
    testSimpleLineFunctor();// 测试线性函数
    testQuadraticFunctor();// 测试二次函数
    testBoothFunctor();// 测试 Booth 函数
    testHimmelblauFunctor();// 测试 Himmelblau 函数

    return0;// 返回 0 表示程序成功结束
}


/*

Refs
https://github.com/daviddoria/Examples/blob/master/c%2B%2B/Eigen/LevenbergMarquardt/CurveFitting.cpp
https://stackoverflow.com/questions/18509228/how-to-use-the-eigen-unsupported-levenberg-marquardt-implementation
https://stackoverflow.com/questions/48213584/understanding-levenberg-marquardt-enumeration-returns
https://www.ultimatepp.org/reference$Eigen_demo$en-us.html
https://ethz-adrl.github.io/ct/ct_doc/doc/html/core_tut_linearization.html
https://robotics.stackexchange.com/questions/20673/why-with-the-pseudo-inverse-it-is-possible-to-invert-the-jacobian-matrix-even-in
http://users.ics.forth.gr/~lourakis/
https://mathoverflow.net/questions/257699/gauss-newton-vs-gradient-descent-vs-levenberg-marquadt-for-least-squared-method
https://math.stackexchange.com/questions/1085436/gauss-newton-versus-gradient-descent
https://stackoverflow.com/questions/34701160/how-to-set-levenberg-marquardt-damping-using-eigen
http://www.netlib.org/minpack/lmder.f
https://en.wikipedia.org/wiki/Test_functions_for_optimization
https://github.com/daviddoria/Examples/blob/master/c%2B%2B/Eigen/LevenbergMarquardt/NumericalDerivative.cpp
https://stackoverflow.com/questions/18509228/how-to-use-the-eigen-unsupported-levenberg-marquardt-implementation
*/

这段代码演示了如何使用 Eigen 库的 Levenberg-Marquardt 算法进行非线性最小二乘优化，通过四个例子展示了不同的函数拟合。下面用数学符号进行总结：

具体例子:

1. 线性拟合 (y = ax + b):

• x = [a, b]ᵀ

   (待优化参数)

• fᵢ(x) = yᵢ - (axᵢ + b)

   (残差函数)

• 目标函数: F(x) = (1/2) * Σᵢ (yᵢ - (axᵢ + b))²

二次曲线拟合 (y = ax² + bx + c):

• x = [a, b, c]ᵀ

   (待优化参数)

• fᵢ(x) = yᵢ - (axᵢ² + bxᵢ + c)

   (残差函数)

• 目标函数: F(x) = (1/2) * Σᵢ (yᵢ - (axᵢ² + bxᵢ + c))²

Booth 函数:

• x = [x, y]ᵀ

   (待优化参数)

• f₁(x) = x + 2y - 7
• f₂(x) = 2x + y - 5

• 目标函数: F(x) = (1/2) * (f₁(x)² + f₂(x)²) = (1/2) * ((x + 2y - 7)² + (2x + y - 5)²) 

Himmelblau 函数:

• x = [x, y]ᵀ

   (待优化参数)

• f₁(x) = x² + y - 11
• f₂(x) = x + y² - 7

• 目标函数: F(x) = (1/2) * (f₁(x)² + f₂(x)²) = (1/2) * ((x² + y - 11)² + (x + y² - 7)²) 

总结:

这段代码通过 Eigen 库实现了 Levenberg-Marquardt 算法，用于解决不同形式的非线性最小二乘问题。每个例子都定义了相应的残差函数 fᵢ(x)，并通过最小化残差平方和来优化参数 x。 代码中使用了数值微分来计算雅可比矩阵。