【Eigen教程】微分（八）

第8章 微分

• 雅可比 Jacobian 矩阵

• 海森 Hessian 矩阵

• 自动微分 Automatic Differentiation

• 数值微分 Numerical Differentiation

• 自动微分与数值微分对比

• 符号微分

雅可比矩阵

Hessian矩阵

接下来你将看到我们如何使用自动微分和数值微分来计算雅可比矩阵。

参考文献：1

https://stats.stackexchange.com/questions/71154/when-an-analytical-jacobian-is-available-is-it-better-to-approximate-the-hessia

自动微分

该代码使用 Eigen 库的自动微分功能，计算多变量函数的导数和雅可比矩阵。具体涉及以下数学内容：

总结：

• 自动微分实现： 代码使用了 Eigen 库的自动微分模块，自动计算复杂函数的导数和雅可比矩阵，避免了手动推导的繁琐过程。

• 应用场景： 这种自动计算导数的能力在优化问题、机器学习和科学计算中非常有用，特别是在需要梯度信息的算法中，例如梯度下降、牛顿法等。

• 优势： 通过模板和泛型编程，代码具有高可重用性和灵活性，可以适用于不同的标量类型和维度。

---

注： 自动微分不同于数值微分（有限差分法）和符号微分。它以程序的计算过程为基础，通过链式法则逐步累积导数，具有计算精度高、效率高的优点。

/*
参考：https://joelcfd.com/automatic-differentiation/
*/

#include <iostream>  // 引入输入输出流库
#include <Eigen/Dense>  // 引入 Eigen 库的密集矩阵模块
#include <unsupported/Eigen/AutoDiff>  // 引入 Eigen 库的自动微分模块

// 定义一个模板函数，对于任意类型 T
template<typenameT>
T MultiVarFunction(const T &x,const T &y)
{
    T z = x *cos(y);// 计算 z = x * cos(y)
    return z;// 返回 z 的值
}

// 示例函数，演示多变量函数的导数计算
voidMultiVarFunctionDerivativesExample()
{
    // 定义自动微分标量类型的 x、y 和 z_derivative
    Eigen::AutoDiffScalar<Eigen::VectorXd> x, y, z_derivative;

    x.value()=2;// 设置 x 的值为 2
    y.value()= M_PI /4;// 设置 y 的值为 π/4

    /*
    Eigen::VectorXd::Unit(2, 0) 表示一个长度为 2，第一位为 1 的单位向量：

    [1]
    [0]

    这意味着我们想要计算相对于第一个变量的导数
    */
    // 指定我们想要计算 dz/dx
    x.derivatives()= Eigen::VectorXd::Unit(2,0);

    /*
    Eigen::VectorXd::Unit(2, 1) 表示一个长度为 2，第二位为 1 的单位向量：

    [0]
    [1]

    这意味着我们想要计算相对于第二个变量的导数
    */
    // 指定我们想要计算 dz/dy
    y.derivatives()= Eigen::VectorXd::Unit(2,1);

    z_derivative =MultiVarFunction(x, y);// 计算函数值和导数

    std::cout <<"AutoDiff:"<< std::endl;// 输出字符串 "AutoDiff:"
    std::cout <<"Function output: "<< z_derivative.value()<< std::endl;// 输出函数值
    std::cout <<"Derivative: \n"<< z_derivative.derivatives()<< std::endl;// 输出导数值
}

// 首先，让我们创建一个通用函数对象。
// 定义一个模板结构体，用于向量函数的计算
template<typename_Scalar,int NX = Eigen::Dynamic,int NY = Eigen::Dynamic>
structVectorFunction{

    typedef _Scalar Scalar;// 定义标量类型

    enum
    {
        InputsAtCompileTime = NX,// 输入维度
        ValuesAtCompileTime = NY   // 输出维度
    };

    // Eigen 库所需的类型定义
    typedef Eigen::Matrix<Scalar, NX,1> InputType;// 输入类型
    typedef Eigen::Matrix<Scalar, NY,1> ValueType;// 输出类型

    // 向量函数
    template<typenameScalar>
    voidoperator()(const Eigen::Matrix<Scalar, NX,1>&x, Eigen::Matrix<Scalar, NY,1>*y)const
    {
        (*y)(0,0)=10.0*pow(x(0,0)+3.0,2)+pow(x(1,0)-5.0,2);// 计算 y 的第一个分量
        (*y)(1,0)=(x(0,0)+1)*x(1,0);// 计算 y 的第二个分量
        (*y)(2,0)=sin(x(0,0))*x(1,0);// 计算 y 的第三个分量
    }
};

// 示例函数，演示雅可比矩阵的计算
voidJacobianDerivativesExample()
{//现在，让我们准备输入矩阵和输出矩阵，并计算雅可比矩阵。
    Eigen::Matrix<double,2,1> x;// 定义 2x1 的输入向量 x
    Eigen::Matrix<double,3,1> y;// 定义 3x1 的输出向量 y
    Eigen::Matrix<double,3,2> fjac;// 定义 3x2 的雅可比矩阵 fjac

    Eigen::AutoDiffJacobian<VectorFunction<double,2,3>> JacobianDerivatives;// 定义自动微分雅可比计算器

    // 设置输入向量 x 的值
    x(0,0)=2.0;// x_0 = 2.0
    x(1,0)=3.0;// x_1 = 3.0

    JacobianDerivatives(x,&y,&fjac);// 计算函数值 y 和雅可比矩阵 fjac

    // 输出指定点处的雅可比矩阵
    std::cout <<"jacobian of matrix at "<<x(0,0)<<","<<x(1,0)<<" is:\n "<< fjac << std::endl;
}

intmain()
{
    MultiVarFunctionDerivativesExample();// 调用多变量函数导数示例
    JacobianDerivativesExample();// 调用雅可比矩阵导数示例
}

这段代码使用了 Eigen 库的自动微分功能，实现了对多变量函数的导数和雅可比矩阵的计算，主要包括以下内容：

总结：

这段代码展示了如何使用 Eigen 库的自动微分模块来计算函数的导数和雅可比矩阵。通过定义自动微分类型的变量，并适当设置导数方向，我们可以方便地获取函数在指定点的导数信息。这对于需要梯度信息的数值优化、机器学习算法和科学计算非常有用。Eigen 库提供的自动微分功能，使得在 C++ 中处理复杂的微分计算变得更加简洁高效。

数值微分

总结：

该代码通过数值微分的方法，计算了多元函数 ff 在指定点处的雅可比矩阵 JJ。它展示了如何使用 Eigen 库的数值微分模块对自定义的向量值函数进行求导，对理解多元函数的偏导数计算和雅可比矩阵的应用具有重要意义。

#include <iostream>  // 引入标准输入输出库
#include <unsupported/Eigen/NumericalDiff>  // 引入 Eigen 库的不支持模块中的数值微分功能

// 通用的函数对象（Functor）模板
template<typename_Scalar,int NX = Eigen::Dynamic,int NY = Eigen::Dynamic>
structFunctor
{
    // 提供给调用者的数值类型（例如 double）和尺寸（输入/输出维度）信息
    typedef _Scalar Scalar;
    enum{
        InputsAtCompileTime = NX,// 编译时已知的输入维度
        ValuesAtCompileTime = NY   // 编译时已知的输出维度
    };
    // 告诉调用者与输入、输出和雅可比矩阵相关的矩阵尺寸
    typedef Eigen::Matrix<Scalar, InputsAtCompileTime,1> InputType;// 输入类型
    typedef Eigen::Matrix<Scalar, ValuesAtCompileTime,1> ValueType;// 输出类型
    typedef Eigen::Matrix<Scalar, ValuesAtCompileTime, InputsAtCompileTime> JacobianType;// 雅可比矩阵类型

    // 本地保存的输入数量和输出数量
    int m_inputs, m_values;

    // 两个构造函数：
    Functor():m_inputs(InputsAtCompileTime),m_values(ValuesAtCompileTime){}// 默认构造函数，使用模板参数的维度
    Functor(int inputs,int values):m_inputs(inputs),m_values(values){}// 带参数的构造函数，手动指定维度

    // 获取函数输入和输出维度的方法
    intinputs()const{return m_inputs;}// 返回输入维度
    intvalues()const{return m_values;}// 返回输出维度

};


// 定义一个具体的函数对象，用于计算向量函数的值
// 向量函数定义为：
// y0 = 10*(x0+3)^2 + (x1-5)^2
// y1 = (x0+1)*x1
// y2 = sin(x0)*x1
structsimpleFunctor:Functor<double>//从上述通用函数对象继承，重写 operator() 并实现你的函数：
{
    simpleFunctor(void):Functor<double>(2,3)// 构造函数，指定输入维度为2，输出维度为3
    {

    }
    // 目标函数的实现

    intoperator()(const Eigen::VectorXd &x, Eigen::VectorXd &fvec)const
    {
        fvec(0)=10.0*pow(x(0)+3.0,2)+pow(x(1)-5.0,2);// 计算 y0
        fvec(1)=(x(0)+1)*x(1);// 计算 y1
        fvec(2)=sin(x(0))*x(1);// 计算 y2
        return0;// 返回 0 表示成功
    }
};


// 一个示例函数，展示如何使用数值微分计算雅可比矩阵
voidsimpleNumericalDiffExample(Eigen::VectorXd &x)
{
    simpleFunctor functor;// 创建函数对象
    Eigen::NumericalDiff<simpleFunctor, Eigen::NumericalDiffMode::Central>numDiff(functor);// 创建数值微分对象，使用中心差分模式
    Eigen::MatrixXd fjac(3,2);// 定义 3x2 的雅可比矩阵
    numDiff.df(x, fjac);// 计算雅可比矩阵
    std::cout <<"jacobian of matrix at "<<x(0)<<","<<x(1)<<" is:\n "<< fjac << std::endl;// 输出雅可比矩阵
}


intmain()
{
    Eigen::VectorXd x(2);// 定义长度为 2 的向量 x
    x(0)=2.0;// 设置 x0 = 2.0
    x(1)=3.0;// 设置 x1 = 3.0
    simpleNumericalDiffExample(x);// 调用示例函数，计算并输出雅可比矩阵
}

该代码演示了如何使用 Eigen 库进行数值微分来计算多元函数的雅可比矩阵。主要步骤和内容包括：

总结：

该代码通过自定义仿函数并利用 Eigen 库的数值微分模块，计算了一个多元函数在指定点处的雅可比矩阵。它展示了如何：

• 定义通用和具体的仿函数以表示目标函数。

• 使用 Eigen::NumericalDiff 对函数进行数值微分计算雅可比矩阵。

• 用于优化、非线性求解等需要雅可比矩阵的场景。

该示例对于理解数值微分、雅可比矩阵的计算以及 Eigen 库的使用具有很好的参考价值。

自动微分与数值微分对比

自动微分（Automatic Differentiation 和 数值微分（Numerical Differentiation是计算函数导数的两种不同技术，在科学计算、机器学习和优化等领域都有广泛的应用。它们各自有优缺点，适用于不同的场景。下面，我们将详细比较这两种方法。

---

定义与原理

自动微分：

• 原理： 自动微分基于对计算过程的解析，通过将基本算子（如加、减、乘、除、sin、cos等）的导数规则嵌入计算图，利用链式法则逐步累积每个操作的导数，最终获得整个函数的精确导数。

• 特点：

  • 精度高：

     自动微分计算的导数具有与解析求导相同的精度，没有截断误差。

  • 效率高：

     相对于符号微分，自动微分避免了表达式膨胀的问题，计算复杂度可控。

  • 易于实现：

     通过重载算术运算符或使用专门的自动微分库，可以在原有代码基础上添加自动微分功能。

数值微分：

• 原理： 数值微分利用有限差分的方法，通过在函数的输入附近取小的增量，计算函数值的变化，以近似求得导数。

• 常用公式：

  

• 特点：

  • 实现简单：

     不需要修改函数本身，只需多次调用函数即可。

  • 近似求解：

     结果是导数的近似值，存在截断误差和舍入误差。

  • 步长选择敏感：

     需要慎重选择增量 hh 的大小，过大或过小都会影响精度。

精度与误差分析

自动微分的精度：

• 解析精度：

   自动微分的结果与解析求导一致，误差仅来自于机器的浮点运算精度。

• 稳定性高：

   不受步长影响，也不受函数复杂度影响。

数值微分的误差：

• 截断误差：

   由泰勒展开忽略高阶项导致，随着步长 hh 的减小而减少。

• 舍入误差：

   由于计算机有限精度，步长过小会导致两个大数相减，放大误差。

• 最佳步长：

   需要在截断误差和舍入误差之间权衡，通常选择 

  

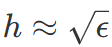
  ，其中 ϵ 是机器精度。

---

计算复杂度与资源消耗

自动微分：

• 计算复杂度：

   相对于原函数的计算，自动微分会有一定的开销，但通常是线性的。

• 内存消耗：

   需要存储中间变量的导数信息，可能增加内存占用。

• 向前模式和反向模式：
  • 向前模式（Forward Mode）：

     适用于输入变量较少的情况，计算每个输入变量对输出的导数。

  • 反向模式（Reverse Mode）：

     适用于输出变量较少的情况，常用于深度学习中的梯度计算。

数值微分：

• 计算复杂度：

   每计算一个导数，需要额外调用函数一次（前向差分）或两次（中心差分）。

• 资源消耗：

   不需要额外的内存，但函数调用次数增加，计算开销较大。

• 高维问题：

   对于高维输入，计算每个维度的导数需要多次函数调用，计算量随维度线性增长。

适用场景与案例分析

自动微分的适用场景：

• 机器学习与深度学习：

   反向传播算法本质上是自动微分的反向模式，被广泛用于训练神经网络。

• 优化算法：

   梯度下降、牛顿法等需要精确的梯度信息，自动微分提供高精度导数。

• 复杂函数：

   函数高度非线性，解析求导困难或不现实的情况下。

案例：

• 在训练深度神经网络时，使用自动微分计算损失函数对权重的梯度，保证训练的稳定性和收敛性。

数值微分的适用场景：

• 黑盒模型：

   函数内部不可见，如外部库函数、实验数据拟合函数等。

• 函数不连续或存在噪声：

   自动微分无法处理不连续点，数值微分可通过适当处理获得近似导数。

• 快速验证：

   在开发初期，快速验证模型的导数特性，不要求高精度。

案例：

• 对于从实验数据得到的插值函数，无法直接求导，使用数值微分估计其斜率，以分析变化趋势。

---

优缺点总结

自动微分：

• 优点：

  • 高精度，无截断误差。

  • 计算效率高，适用于大型计算。

  • 可处理复杂的函数结构。

• 缺点：

  • 实现复杂度较高，需要特殊的数据类型和库。

  • 对于黑盒函数或存在分支的代码无法处理。

  • 可能增加内存占用。

数值微分：

• 优点：

  • 实现简单，适用于任何可计算函数。

  • 不需要了解函数的内部结构。

  • 适用于快速原型和测试。

• 缺点：

  • 精度低，存在截断和舍入误差。

  • 计算成本高，尤其在高维情况下。

  • 对步长敏感，选择不当可能导致误差增大。

---

补充说明

• 符号微分（Symbolic Differentiation）： 除了自动微分和数值微分外，符号微分通过解析的方法求导，生成导数的解析表达式。虽然精度高，但对复杂函数可能产生表达式膨胀，计算效率低。

• 混合方法： 在实际应用中，可能结合自动微分和数值微分。例如，对易于自动微分的部分使用自动微分，对黑盒部分使用数值微分。

• 工具与库： 常用的自动微分库包括：

  • C++：

     Eigen、Ceres、ADOL-C、Stan Math Library。

  • Python：

     TensorFlow、PyTorch、JAX、Autograd。

  • Julia：

     ForwardDiff.jl、ReverseDiff.jl。

---

结论

• 选用自动微分： 当函数可以逐步分解为基本操作，且需要高精度导数时，自动微分是首选，特别是在优化和机器学习中。

• 选用数值微分： 当函数为黑盒、无法解析或自动微分实现困难时，数值微分提供了一种简单可行的近似方法。

建议： 在实际问题中，应根据需求、精度要求、计算资源和函数特性，选择最适合的方法。对于需要高度精确导数的大规模问题，自动微分的优势更加明显。而在函数复杂度较低、精度要求不高或实现成本受限的情况下，数值微分也是一种有效的工具。

---

延伸阅读：

• 高阶导数与偏导数： 自动微分不仅可以计算一阶导数，还可以扩展到高阶导数和偏导数，进一步支持高阶优化算法。

• 自动微分的方向： 了解向前模式和反向模式的区别，选择适合具体应用的自动微分方向。

• 性能优化： 在实际应用中，自动微分的实现可以结合代码优化技巧，提高计算效率，如利用稀疏矩阵、并行计算等。

• 理论基础： 深入研究自动微分的数学原理，如计算图、链式法则、Adjoint 方法等，能够更好地理解其工作机制。

通过对自动微分和数值微分的深入比较，我们可以更全面地掌握计算导数的工具，提升在科学计算和工程应用中的效率和准确性。

符号微分

符号微分（Symbolic Differentiation 是一种使用数学符号和公式，对函数进行解析求导的技术。与自动微分和数值微分不同，符号微分直接操作函数的解析表达式，通过应用微积分的规则，得到导数的符号表达式。符号微分在计算代数系统（如 Mathematica、Maple、SymPy 等）中得到了广泛的应用。

---

一、符号微分的原理

符号微分基于微积分中的求导规则，通过对函数的解析表达式逐项应用导数公式，得到导函数的解析形式。主要应用的求导规则包括：

二、符号微分的步骤

1. 解析表示：将待求导的函数表示为符号表达式，方便后续操作。

2. 分解函数：根据求导规则，将复杂的函数分解为基本函数的组合（如和、差、积、商、复合）。

3. 逐项求导：对分解后的每一项应用相应的求导公式和法则。

4. 简化结果：将得到的导数表达式进行代数化简，得到最简形式。

---

三、符号微分的示例

四、符号微分的优缺点

优点：

1. 精确性：符号微分得到的是导数的解析表达式，具有精确性。

2. 通用性：一次求导可以适用于任意输入值，不需要重复计算。

3. 可分析性：导数表达式可用于进一步的数学分析，如极值、拐点等的求解。

缺点：

1. 复杂性增长（表达式膨胀）：对于复杂的函数，符号微分可能产生非常庞大的表达式，难以简化。

2. 计算资源高：处理复杂表达式需要大量的计算资源，可能导致运算时间长或内存消耗大。

3. 实现难度：需要符号计算的支持，通常需要使用专门的计算代数系统。

---

五、符号微分的应用

1. 数学分析：求解函数的导数、积分，分析函数的性质，如单调性、凹凸性等。

2. 物理学与工程学：推导公式、分析系统动态行为。

3. 控制理论：设计控制器，需要解析求导以获得系统的灵敏度和稳定性分析。

4. 机器学习：在某些情形下，需要解析导数来理解模型的行为。

---

六、符号微分与其他求导方法的比较

1. 与自动微分比较：

• 符号微分

  提供解析表达式，适合数学推导和理论分析。

• 自动微分

  计算数值导数，适合数值计算和优化，避免了表达式膨胀。

与数值微分比较：

• 符号微分

  精度高，无截断误差，但可能计算复杂度高。

• 数值微分

  实现简单，但有截断和舍入误差，对步长敏感。

---

七、符号计算软件

由于符号微分的计算复杂性，一般借助计算机代数系统（CAS）来完成。常用的软件包括：

1. Mathematica：

• 功能强大的符号计算软件，支持复杂函数的符号微分、积分、极限等。

Maple：

• 提供全面的符号和数值计算功能，适合工程和科学研究。

SymPy（Python库）：

• 开源的Python符号计算库，方便在Python环境中进行符号计算。

Maxima：

• 开源的符号计算软件，支持符号求导、积分、方程求解等。

---

八、实践示例（使用 SymPy）

以下使用 Python 的 SymPy 库进行符号微分的示例：

from sympy import symbols, diff, sin, cos, exp

# 定义符号变量
x, y = symbols('x y')

# 定义函数
f = x**3 * sin(x) * exp(x)

# 对 x 求导
df_dx = diff(f, x)

print("函数 f(x) 为：", f)
print("对 x 求导后得到：", df_dx)

输出：

函数 f(x) 为： x**3 * sin(x) * exp(x)
对 x 求导后得到： x**3 * cos(x) * exp(x) + x**3 * sin(x) * exp(x) + 3*x**2 * sin(x) * exp(x)

---

九、符号微分的局限性

1. 表达式膨胀：对于嵌套层次深、高度非线性的函数，符号微分会产生极其复杂的表达式，难以处理。

2. 不可微函数：对于函数中包含不可微的部分（如绝对值、分段函数等），符号微分可能无法直接处理，需要特殊处理。

3. 程序代码求导：符号微分主要针对数学表达式，对于以程序代码形式表示的函数，难以直接应用。

---

十、符号微分的改进方法

1. 表达式优化：使用智能的表达式简化算法，减小表达式的复杂度。

2. 分块处理：将大型表达式分解为可管理的小块，分别求导后再组合。

3. 混合方法：结合符号微分和数值方法，对关键部分进行符号求导，其余部分采用数值方法。

---

总结

符号微分是数学分析中的重要工具，通过解析的方法精确地求解导数，为深入理解函数的行为提供了有力的手段。虽然在处理复杂函数时存在计算上的挑战，但借助计算代数系统，符号微分在科学研究、工程应用和教育领域都有着广泛的应用。

在实际应用中，应根据具体需求，选择适当的求导方法。对于需要解析表达式进行理论分析的情况，符号微分是不可或缺的工具。而在数值计算和优化中，自动微分和数值微分可能更为实用。

---

推荐阅读：

• 《微积分》教材

  ：深入理解求导规则和微积分原理。

• 符号计算教材

  ：了解计算代数系统的原理和应用。

• SymPy 官方文档

  ：学习如何在 Python 中进行符号计算。

• 《Mathematica 编程指南》

  ：掌握使用 Mathematica 进行符号微分的方法。

通过对符号微分的深入学习，可以提升数学素养，为解决复杂的科学与工程问题奠定坚实的基础。