基于人工鱼群优化算法的最优路径规划matlab仿真

fpga和matlab

已于 2024-04-10 23:12:49 修改

阅读量1.2k

点赞数 4

分类专栏：部分上传资源仿真展示与分析板块7:优化类问题文章标签：算法人工鱼群优化最优路径规划

于 2024-04-10 23:07:54 首次发布

本文链接：https://blog.youkuaiyun.com/ccsss22/article/details/137614931

版权

板块7:优化类问题同时被 2 个专栏收录

141 篇文章

订阅专栏

部分上传资源仿真展示与分析

136 篇文章

订阅专栏

人工鱼群优化算法（Artificial Fish Swarm Algorithm, AFSA）是一种模仿自然界鱼类集群行为的启发式优化方法，常用于解决复杂的路径规划问题。在最优路径规划中，AFSA旨在寻找一条从起点到终点的路径，该路径满足特定的优化目标（如最短距离、最小能耗、最大安全性等）。与狮子和猴子不同，在像鱼类这种动物物种中没有领导者，每个成员都有自我组织的行为。鱼对它们的群体和环境一无所知，通过相邻成员之间的数据交换在环境中随意移动，这种交互作用为鱼群优化带来了更多的复杂性。AFSA具有容错性和灵活性等特点，它在资源均衡、模糊聚类、数据挖掘、扩频码估计、DNA编码序列优化、信号处理、图像处理、改进神经网络、作业调度等方面有着广泛的应用。AFSA具有收敛速度快、效率高等优点，同时也存在时间复杂度高、全局搜索与局部搜索不平衡等缺点。

1. 人工鱼群优化算法的基本原理

AFSA模拟了鱼类群体在自然环境中的觅食、追尾、聚群和随机游动四种行为。这些行为通过数学模型转化为搜索策略，用于探索和优化潜在解空间。

1.1 觅食行为

鱼类会主动向食物源游动。在优化问题中，食物浓度F(x,y) 表示解的质量，通常与目标函数f(x,y) 呈反比：

个体鱼 i 向食物浓度高的区域移动，其速度更新公式为：

1.2 追尾行为

鱼类会跟随附近同伴游动。个体鱼 i 选择邻居鱼j 进行追尾，其速度更新公式为：

1.3 聚群行为

鱼类倾向于保持与邻近伙伴的距离。个体鱼 i 与其邻居 j 之间的距离Dij 应保持在一定范围内：

1.4 随机游动

鱼类偶尔进行无规则游动以探索新区域。个体鱼 i 随机扰动其速度：

2.基于AFSA的最优路径规划

在路径规划问题中，路径被视为由一系列离散节点组成的序列，每个节点代表空间中的一个位置。AFSA应用于路径规划时，需进行如下适应性调整：

2.1 解编码

将路径表示为一个向量或矩阵，每个元素对应一个节点编号。例如，路径P=[n1,n2,...,nN]，其中 ni 是第 i 个节点的编号。

2.2 目标函数

定义路径的目标函数f(P)，反映路径的优劣。目标函数可以是路径长度、总能耗、安全性指标等的加权和：

2.3 空间约束与障碍处理

确保路径符合实际空间约束（如转弯半径、最大速度限制等），并避免碰撞障碍物。这通常通过在目标函数中添加惩罚项或在速度更新过程中实施障碍规避策略实现。

2.4 初始化与迭代

初始化一群人工鱼（即一组初始路径），然后按照觅食、追尾、聚群和随机游动行为进行迭代更新，直至满足终止条件（如最大迭代次数、收敛阈值等）。

3.MATLAB核心程序

.................................................................................
CityPosition=[16.47,96.10;%从上到下，依次是14个城市的坐标，每一行一个城市。
              16.47,94.44;
              20.09,92.54;
              22.39,93.37;
              25.23,97.24; 
              22.00,96.05;
              20.47,97.02;
              17.20,96.29;
              16.30,97.38;
              14.05,98.12;
              16.53,97.38;
              21.52,95.59;
              19.41,97.13;
              20.09,92.55];
 CityNum=length(CityPosition);%城市个数
 DNAN=100;                   %同一个城市之间的距离定义为无穷大
 for i=1:CityNum              %算出每条边的长度
     edge(i,i)=DNAN;
     for j=i+1:CityNum
         edge(i,j)=sqrt(sum((CityPosition(i,:)-CityPosition(j,:)).^2));
         edge(j,i)=edge(i,j);
     end
 end
 for i=1:FishNum             %对所有人工鱼进行初始化
     X(i,:)=Inital(CityNum);
 end
 Best=1000;
 for NC=1:Max_gen
     Besty(NC)=1000;
     for i=1:FishNum
         [Xi,flag1]=follow(X,FishNum,Visual,deta,i,edge);%首先偿试追尾
         if(flag1==0) %追尾失败
             Visual2=floor(Visual*(1-NC/Max_gen));
             [Xi,flag2]=prey(X,CityNum,i,Visual,trynumber,edge);%再偿试觅食
             if(flag2==0) %觅食失败
                   [Xi,flag3]=swarm(X,FishNum,CityNum,Visual,deta,i,edge);%再偿试聚群
                   if(flag3==0)%聚群失败
                        Xi=X(i,:);%无奈，静止不动，这是对算法的一个改进
                   end
               end
           end
           X(i,:)=Xi;
           Yi=evaluate(Xi,edge);
           if(Yi<Besty(NC))
               Besty(NC)=Yi;%每次最优解
           end
           if(Yi<Best)
               Best=Yi;     %全局最优解
               Bestpath=Xi;
           end
                          
       end
          disp(['第',num2str(NC),'次迭代,得出的最优值：',num2str(Besty(NC))]);
   end
   t_train=toc;%结束记时
   s=num2str(Bestpath(1));
   for i=2:CityNum
       s=strcat(s,'->');
       s=strcat(s,num2str(Bestpath(i)));
   end
   s=strcat(s,'->');
   s=strcat(s,num2str(Bestpath(1)));
   clc

   disp(['得出的最优路径:',s,',最优值:',num2str(Best)]);
   plot(Besty);
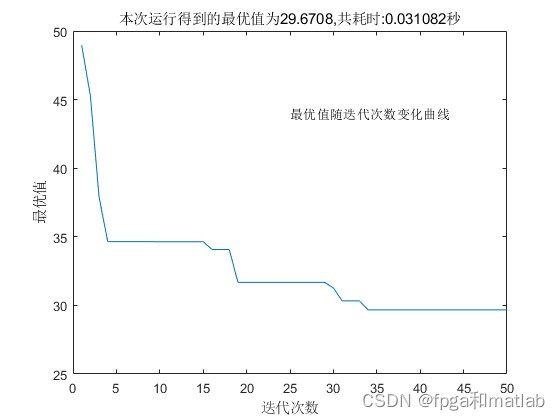
   title(['本次运行得到的最优值为',num2str(Best),',共耗时:',num2str(t_train),'秒']);%x，
   text(floor(Max_gen/2),44,'最优值随迭代次数变化曲线');
   xlabel('迭代次数');
   ylabel('最优值');
   up4067