基于机器学习的Iris花卉数据分类matlab仿真

目录

1.Iris数据集介绍

2.机器学习

2.1 K近邻（KNN）算法

2.2 决策树算法

3.matlab程序

4.仿真结果

---

1.Iris数据集介绍

       Iris数据集是机器学习领域中的一个经典数据集，它包含了三种不同类型的鸢尾花（Iris）的四个特征：花萼长度、花萼宽度、花瓣长度和花瓣宽度。基于这些特征，我们可以利用机器学习算法对鸢尾花的种类进行分类。

      Iris数据集是统计学家Ronald Fisher于1936年引入的经典多类分类问题的数据集，包含150个样本，每个样本有4个特征（花萼长度、花萼宽度、花瓣长度、花瓣宽度）以及一个标签（鸢尾花种类：Setosa、Versicolour或Virginica）。这个数据集常被用于演示和验证各种机器学习算法，如决策树、支持向量机、K近邻法以及神经网络等。

         Iris数据集包含了三种鸢尾花（Iris setosa、Iris virginica和Iris versicolor）的50个样本，每种各50个。对于每个样本，都有四个特征被测量和记录：

1. 萼片长度（sepal length）
2. 萼片宽度（sepal width）
3. 花瓣长度（petal length）
4. 花瓣宽度（petal width）

这些特征的单位都是厘米（cm）。每个样本都明确标记了其所属的鸢尾花种类。

       调用数据集的代码如下：

function [X, y] = loadData()

data = csvread('iris.data');
m = size(data, 1);
n = size(data, 2);
rndIDX = randperm(m); 

newSample = data(rndIDX(1:m), :); 

X = newSample(:,1:4);
y = newSample(:,5);

end

       数据集内容如下：

5.1,3.5,1.4,0.2,1
4.9,3.0,1.4,0.2,1
4.7,3.2,1.3,0.2,1
4.6,3.1,1.5,0.2,1
5.0,3.6,1.4,0.2,1
5.4,3.9,1.7,0.4,1
4.6,3.4,1.4,0.3,1
5.0,3.4,1.5,0.2,1
4.4,2.9,1.4,0.2,1
4.9,3.1,1.5,0.1,1
5.4,3.7,1.5,0.2,1
4.8,3.4,1.6,0.2,1
4.8,3.0,1.4,0.1,1
4.3,3.0,1.1,0.1,1
5.8,4.0,1.2,0.2,1
5.7,4.4,1.5,0.4,1
5.4,3.9,1.3,0.4,1
5.1,3.5,1.4,0.3,1
5.7,3.8,1.7,0.3,1
5.1,3.8,1.5,0.3,1
5.4,3.4,1.7,0.2,1
5.1,3.7,1.5,0.4,1
4.6,3.6,1.0,0.2,1
5.1,3.3,1.7,0.5,1
4.8,3.4,1.9,0.2,1
5.0,3.0,1.6,0.2,1
5.0,3.4,1.6,0.4,1
5.2,3.5,1.5,0.2,1
5.2,3.4,1.4,0.2,1
4.7,3.2,1.6,0.2,1
4.8,3.1,1.6,0.2,1
5.4,3.4,1.5,0.4,1
5.2,4.1,1.5,0.1,1
5.5,4.2,1.4,0.2,1
4.9,3.1,1.5,0.2,1
5.0,3.2,1.2,0.2,1
5.5,3.5,1.3,0.2,1
4.9,3.6,1.4,0.1,1
4.4,3.0,1.3,0.2,1
5.1,3.4,1.5,0.2,1
5.0,3.5,1.3,0.3,1
4.5,2.3,1.3,0.3,1
4.4,3.2,1.3,0.2,1
5.0,3.5,1.6,0.6,1
5.1,3.8,1.9,0.4,1
4.8,3.0,1.4,0.3,1
5.1,3.8,1.6,0.2,1
4.6,3.2,1.4,0.2,1
5.3,3.7,1.5,0.2,1
5.0,3.3,1.4,0.2,1
7.0,3.2,4.7,1.4,2
6.4,3.2,4.5,1.5,2
6.9,3.1,4.9,1.5,2
5.5,2.3,4.0,1.3,2
6.5,2.8,4.6,1.5,2
5.7,2.8,4.5,1.3,2
6.3,3.3,4.7,1.6,2
4.9,2.4,3.3,1.0,2
6.6,2.9,4.6,1.3,2
5.2,2.7,3.9,1.4,2
5.0,2.0,3.5,1.0,2
5.9,3.0,4.2,1.5,2
6.0,2.2,4.0,1.0,2
6.1,2.9,4.7,1.4,2
5.6,2.9,3.6,1.3,2
6.7,3.1,4.4,1.4,2
5.6,3.0,4.5,1.5,2
5.8,2.7,4.1,1.0,2
6.2,2.2,4.5,1.5,2
5.6,2.5,3.9,1.1,2
5.9,3.2,4.8,1.8,2
6.1,2.8,4.0,1.3,2
6.3,2.5,4.9,1.5,2
6.1,2.8,4.7,1.2,2
6.4,2.9,4.3,1.3,2
6.6,3.0,4.4,1.4,2
6.8,2.8,4.8,1.4,2
6.7,3.0,5.0,1.7,2
6.0,2.9,4.5,1.5,2
5.7,2.6,3.5,1.0,2
5.5,2.4,3.8,1.1,2
5.5,2.4,3.7,1.0,2
5.8,2.7,3.9,1.2,2
6.0,2.7,5.1,1.6,2
5.4,3.0,4.5,1.5,2
6.0,3.4,4.5,1.6,2
6.7,3.1,4.7,1.5,2
6.3,2.3,4.4,1.3,2
5.6,3.0,4.1,1.3,2
5.5,2.5,4.0,1.3,2
5.5,2.6,4.4,1.2,2
6.1,3.0,4.6,1.4,2
5.8,2.6,4.0,1.2,2
5.0,2.3,3.3,1.0,2
5.6,2.7,4.2,1.3,2
5.7,3.0,4.2,1.2,2
5.7,2.9,4.2,1.3,2
6.2,2.9,4.3,1.3,2
5.1,2.5,3.0,1.1,2
5.7,2.8,4.1,1.3,2
6.3,3.3,6.0,2.5,3
5.8,2.7,5.1,1.9,3
7.1,3.0,5.9,2.1,3
6.3,2.9,5.6,1.8,3
6.5,3.0,5.8,2.2,3
7.6,3.0,6.6,2.1,3
4.9,2.5,4.5,1.7,3
7.3,2.9,6.3,1.8,3
6.7,2.5,5.8,1.8,3
7.2,3.6,6.1,2.5,3
6.5,3.2,5.1,2.0,3
6.4,2.7,5.3,1.9,3
6.8,3.0,5.5,2.1,3
5.7,2.5,5.0,2.0,3
5.8,2.8,5.1,2.4,3
6.4,3.2,5.3,2.3,3
6.5,3.0,5.5,1.8,3
7.7,3.8,6.7,2.2,3
7.7,2.6,6.9,2.3,3
6.0,2.2,5.0,1.5,3
6.9,3.2,5.7,2.3,3
5.6,2.8,4.9,2.0,3
7.7,2.8,6.7,2.0,3
6.3,2.7,4.9,1.8,3
6.7,3.3,5.7,2.1,3
7.2,3.2,6.0,1.8,3
6.2,2.8,4.8,1.8,3
6.1,3.0,4.9,1.8,3
6.4,2.8,5.6,2.1,3
7.2,3.0,5.8,1.6,3
7.4,2.8,6.1,1.9,3
7.9,3.8,6.4,2.0,3
6.4,2.8,5.6,2.2,3
6.3,2.8,5.1,1.5,3
6.1,2.6,5.6,1.4,3
7.7,3.0,6.1,2.3,3
6.3,3.4,5.6,2.4,3
6.4,3.1,5.5,1.8,3
6.0,3.0,4.8,1.8,3
6.9,3.1,5.4,2.1,3
6.7,3.1,5.6,2.4,3
6.9,3.1,5.1,2.3,3
5.8,2.7,5.1,1.9,3
6.8,3.2,5.9,2.3,3
6.7,3.3,5.7,2.5,3
6.7,3.0,5.2,2.3,3
6.3,2.5,5.0,1.9,3
6.5,3.0,5.2,2.0,3
6.2,3.4,5.4,2.3,3
5.9,3.0,5.1,1.8,3

2.机器学习

       在Iris花卉数据分类中，我们可以采用多种机器学习分类算法，如K近邻（KNN）、决策树、支持向量机（SVM）和神经网络等。下面以KNN和决策树为例，详细介绍其原理。

2.1 K近邻（KNN）算法

        KNN算法是一种基于实例的学习方法，它的基本思想是：如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别。KNN算法的距离度量通常采用欧氏距离。

        在KNN算法中，我们需要选择一个合适的k值，并通过计算待分类样本与训练集中每个样本的距离，找到最近的k个邻居。然后，根据这k个邻居的类别，通过多数投票的方式确定待分类样本的类别。

2.2 决策树算法

       决策树算法是一种基于树形结构的分类算法，它通过一系列的判断条件对数据进行划分，直到达到终止条件（如所有样本属于同一类别或达到最大深度等）。决策树的构建过程包括特征选择、决策树生成和决策树剪枝等步骤。       

       在特征选择阶段，我们需要选择一个最优特征作为划分标准。常用的特征选择准则有信息增益、增益率和基尼指数等。

        在决策树生成阶段，我们根据选定的特征选择准则递归地构建决策树。当达到终止条件时，将当前节点标记为叶节点，并将其类别标记为该节点所含样本最多的类别。在决策树剪枝阶段，我们可以通过预剪枝或后剪枝的方式对决策树进行简化，以防止过拟合。

3.matlab程序

............................................
[X, y] = loadData();

%sizes
m = size(X, 1);
n = size(X, 2);

%number of classes
k = 3;


trainingSetRatio = 0.7;
[Xtrain, yTrain, Xtest, yTest] = getTrainingAndTestSet(X, y, trainingSetRatio);


%initialise theta
all_theta = zeros(k, n);
alpha = 0.01;
iterations = 1500;

[all_theta, J_history] = gradientDescent(Xtrain, yTrain, k, all_theta, alpha, iterations);

figure;
plot(1:iterations, J_history(:,1), '-b', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J for classifier 1');

figure;
plot(1:iterations, J_history(:,2), '-r', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J for classifier 2');

figure;
plot(1:iterations, J_history(:,3), '-g', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J for classifier 3');

%predict
predictions = predict(Xtest, all_theta);

compare = [predictions yTest]

total = size(yTest, 1)
correct = sum(predictions==yTest)
accuracy = (correct/total)*100
up4041

4.仿真结果

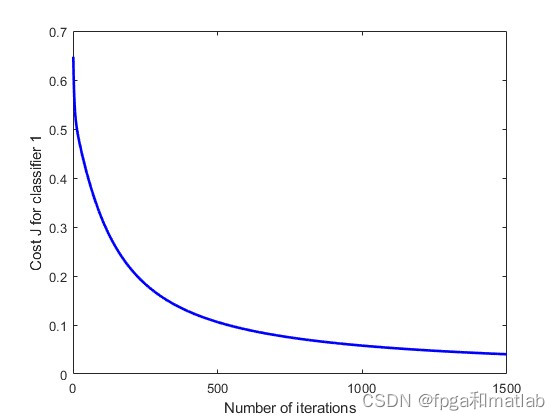
       在构建完分类模型后，通过多次训练和验证来评估模型在不同数据集上的性能。网格搜索和随机搜索则是通过搜索参数空间来找到最优参数组合的方法。