目录
1.巴特沃斯IIR滤波器
巴特沃斯滤波器以其平坦的频率响应而著名,即在通带内没有波纹。它的设计目的是在通带和阻带之间提供尽可能平滑的转换。巴特沃斯滤波器是无限冲激响应(IIR)滤波器的一种,它利用了反馈机制。巴特沃斯滤波器是一种具有最大平坦度响应(即没有波纹)的滤波器。其特点是在通带内频率响应尽可能平坦,而在阻带内逐渐下降为零。
巴特沃斯滤波器是一种具有最平坦通带响应的理想滤波器类型,在通带内具有最大平坦度且随着频率增加,幅频响应单调递减。在设计过程中,其极点分布在一个半径为11的单位圆上,并均匀分布在角度上,使得幅频响应在截止频率处呈−3−3dB衰减,并保持最大的平坦度。
对于一个N阶低通巴特沃斯滤波器,传递函数可以表示为:

name = 'Butterworth';
%find the order of the butterwoth filter
%specify parameters
%cutoff freq of 2750 Hz normalized
Wp = 2750/(Fs/2);
%stopband 3000 Hz normalized
Ws = 3000/(Fs/2);
%passband ripple dB
Rp = .1;
%stopband attentuation dB
Rs = 100;
%find the butter order in normalized frequency and the cutoff
[n,Wn] = buttord(Wp,Ws,Rp,Rs);
%calculate butterworth zeros, poles, and gain k
[z,p,k] = butter(n,Wn);
%calculate the second order section respesentation of the filter
sos = zp2sos(z,p,k);
%view the filter characteristics
fvtool(sos)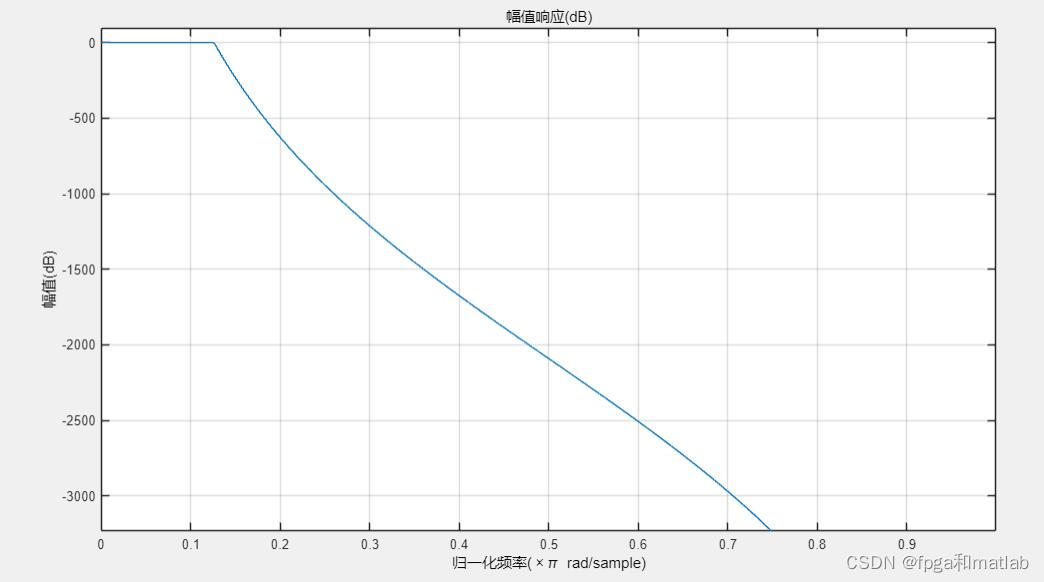
2.Kaiser窗FIR滤波器
凯泽窗法是一种用于设计有限冲激响应(FIR)滤波器的方法。通过调整凯泽窗参数,可以在降低旁瓣电平和增加主瓣宽度之间进行权衡。凯泽窗的一个关键特点是它可以通过一个参数来控制窗函数的形状,从而影响滤波器的性能。
Kaiser窗是一种用于设计有限脉冲响应(FIR)滤波器时窗口函数的选择,尤其适用于需要控制过渡带宽度和峰值幅度失真的情况。Kaiser窗通过可调参数β来调整窗口形状以满足特定的设计要求。对于长度为M的FIR滤波器,其滤波器系数可以通过以下方式计算得到:

- h[n] 是第n个滤波器系数。
- I0(x) 是零阶修正贝塞尔函数。
- β 是根据所需的阻带衰减和过渡带宽度确定的参数。
- α 是过渡带宽度与滤波器长度之间的关系参数,决定了过渡带边缘相对于奈奎斯特频率的位置。
FIR滤波器的设计通常涉及到窗函数法和频率采样法。在窗函数法中,理想滤波器的脉冲响应被截断并乘以一个窗函数以减少吉布斯现象(Gibbs Phenomenon)。Kaiser窗提供了一种有效的方法来控制旁瓣级别和主瓣宽度。
%KAISER
%ex 7.6.1
name = 'Kaiser';
%ripple of 1/100e3 same as parks mclellan and butterworth design
%ripple is same for pass and stopband for Kaiser window
delta = 1/100e3;
%normalized edge of passband
wp = 2750*pi/(Fs/2);
%normalized beginnihdng of stopband
ws = 3000*pi/(Fs/2);
%find symmetric cutoff, average of normalized frequencies
wc = (wp+ws)/2;
%find the width of the transition band
deltaw = ws-wp;
%find linear gain A
A = -20*log10(delta);
%find beta B
if A > 50
beta = .1102*(A-8.7);
elseif A >= 21 && A <=50
beta = .5842*(A-21)^0.4+.07886*(A-21);
elseif A < 21
beta = 0;
end
%find length parameter M, find length len, find alpha
M = ceil((A-8)/(2.285*deltaw));
len = M+1;
%create kaiser window and apply it to the desired impulse response to form
%the filter
%create x axis, of samples
n=(0:M).';
%create kaiser coefficients wn
wn = kaiser(len,beta);
%create ideal impulse response
hdn = wc/pi*sinc((n-M/2)*wc/pi);
%multiply the desired impulse response by the filter coefficients
hd = hdn.*wn;
%view the filter characteristics
fvtool(hd)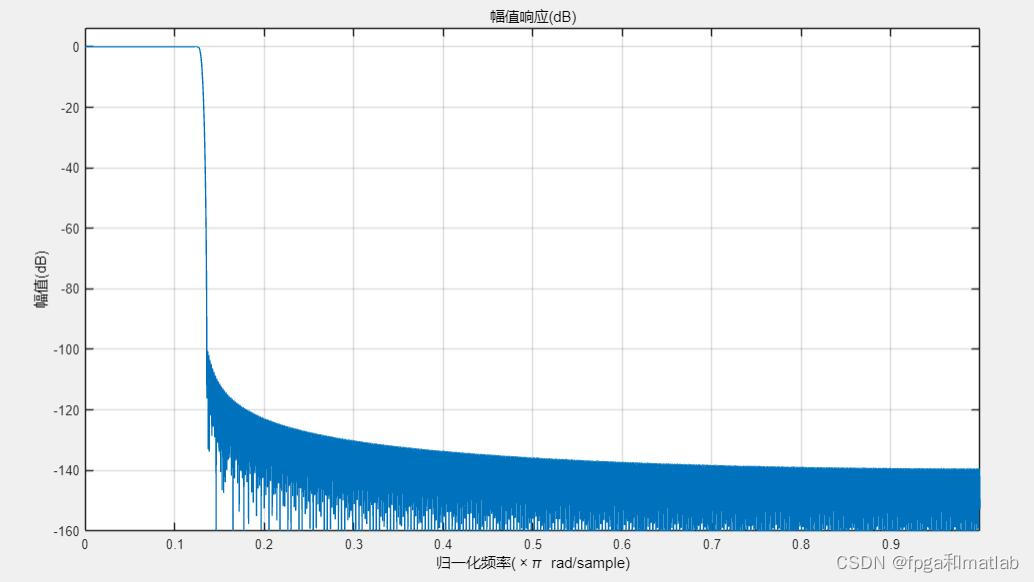
3.Parks-McClellan等波纹FIR滤波器
帕克斯-麦克莱伦算法是一种用于设计FIR滤波器的优化技术,它通过切比雪夫逼近法最小化滤波器在通带和阻带的最大误差,从而在通带和阻带实现等波纹特性。Parks-McClellan算法用于设计具有等波纹特性(即过渡带内幅度波动保持一致)的有限脉冲响应滤波器。该算法基于Chebyshev多项式和Remez交换算法,寻找最优的滤波器系数集合,使滤波器在整个通带、过渡带和阻带区域达到预设的性能指标。
Parks-McClellan算法的基本思想是使用交替定理(Alternation Theorem),该定理指出最优滤波器的频率响应在通带和阻带边界处具有交替的极大值和极小值。算法通过迭代地调整滤波器的系数来满足这些条件。
算法的具体细节较为复杂,但基本步骤如下:
- 初始化一个滤波器系数向量。
- 计算滤波器的频率响应。
- 检查通带和阻带内的误差是否满足要求。
- 如果不满足要求,则调整滤波器系数并重复步骤2和3。
- 当满足要求时,输出滤波器系数。
由于Parks-McClellan算法涉及到迭代过程和复杂的数学运算,因此很难在这里给出详细的数学公式。然而,该算法在许多信号处理软件包中都有实现,如MATLAB的firpm函数。
%PARKS
name = 'Parks-McClellan';
%Passband ripple
rp = .1;
%Stopband ripple
rs = 100;
%Cutoff frequencies, [pass stop]
f = [2750 3000].';
%Desired amplitudes [pass stop]
a = [1 0].';
%change ripples from db to gain
dev = [(10^(rp/20)-1)/(10^(rp/20)+1) 10^(-rs/20)].';
[n,fo,ao,w] = firpmord(f,a,dev,Fs);
b = firpm(n,fo,ao,w);
%view the filter characteristics
fvtool(b)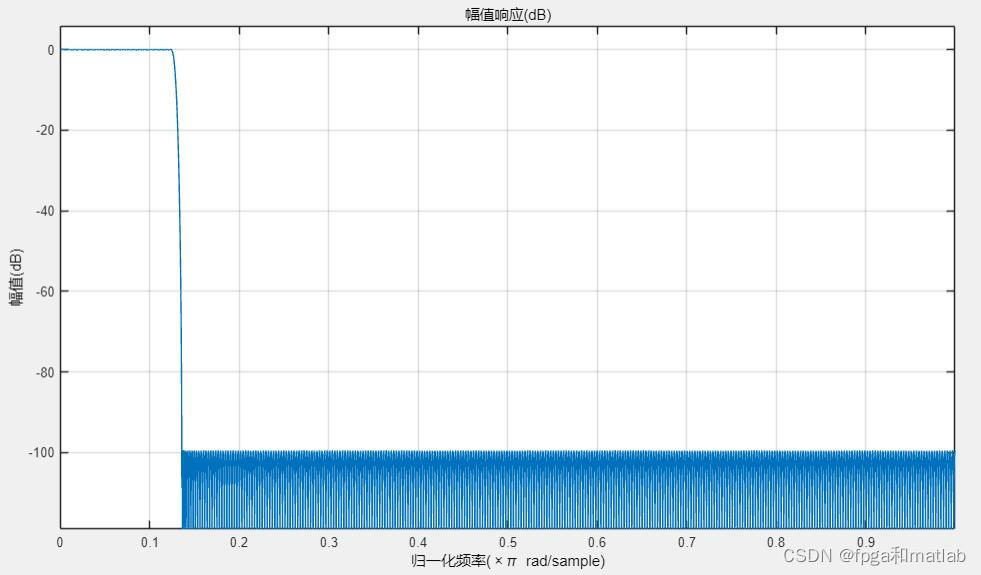











 本文介绍了巴特沃斯IIR滤波器的平坦频率响应特性,Kaiser窗FIR滤波器的窗函数调整策略,以及Parks-McClellan算法如何设计等波纹FIR滤波器。着重讨论了这些滤波器在信号处理中的应用和设计过程。
本文介绍了巴特沃斯IIR滤波器的平坦频率响应特性,Kaiser窗FIR滤波器的窗函数调整策略,以及Parks-McClellan算法如何设计等波纹FIR滤波器。着重讨论了这些滤波器在信号处理中的应用和设计过程。

















 711
711

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










