目录
3. 最大似然估计(Maximum Likelihood Estimation, MLE)
在数字通信系统中,二进制相移键控(Binary Phase Shift Keying,BPSK)是一种简单且广泛使用的调制方式。然而,在实际的通信链路中,由于信道失真、噪声干扰以及收发两端的时钟偏差,接收到的信号往往会发生畸变,导致解调性能下降。为了恢复发送的数据,接收端需要进行定时恢复,即确定最佳的采样时刻。
1.BPSK调制原理
BPSK是一种数字调制方式,其中每个比特的信息通过相位的变化来表示。在BPSK调制中,二进制“0”和“1”分别映射到相位0和π(或相反)。在BPSK系统中,一个比特信息通过改变载波信号的相位来传输。假设二进制数据为d(t),其值可以是±1,对应的调制信号s(t)为:
![]()
其中,f_c 是载波频率,θ_0 是初始相位。
2. 定时偏移问题与定时恢复
在实际的通信系统中,由于收发两端的时钟不完全同步,接收端采样时可能会偏离最佳的采样点。这种偏差会导致解调性能下降,甚至无法正确恢复发送的数据。因此,定时恢复是数字通信系统中的一个关键问题。
接收端接收到的信号r(t)通常会受到信道延迟的影响,即存在一个未知的定时偏移τ:
![]()
其中,n(t) 表示噪声干扰。为了准确解调,必须首先确定并消除这个定时偏移。
3. 最大似然估计(Maximum Likelihood Estimation, MLE)
最大似然估计是一种统计估计方法,它的基本思想是:在给定观测数据的情况下,选择使得观测数据出现的概率最大的参数值作为估计结果。在BPSK解调系统中,我们可以利用最大似然估计来估计最佳的采样时刻。对于BPSK系统,最大似然准则要求我们找到使接收信号概率最大的定时偏移τ。设接收到的一个符号周期内的采样点序列为{r(1), r(2), ..., r(N)},则每个采样点对应的最大似然函数可以表示为:
![]()
在AWGN信道下,单个采样点的概率密度函数为高斯分布,因此:

最大化上述似然函数就是要找到使得所有采样点与理论信号之间误差平方和最小的τ值,即:
![]()
这是一个非线性优化问题,通常可以通过导数法求解或者采用滑动窗口的快速算法如早迟门检测器(Early-Late Gate)或相关峰搜索等方法近似解决。
在一阶差分相关器中,定义两组不同延迟的采样序列:

当定时正确时,Early样本和Late样本的期望值均等于二进制符号的变化,通过比较这两者幅值大小,可以得到最大似然下的定时位置。
实际应用中,最大似然定时恢复可能还需要结合循环前缀、训练序列等手段进行更为精确的定时估计,以应对复杂的无线通信环境。
4. matlab程序
..............................................................................
PN_length=G;
Rc_estimate=Rc;
fo_estimate=fo;
%********************************解调至基带**************************************%
DSSS_BASEBAND=demodulation_bpsk(X_N,fo_estimate,Rc_estimate,delay_lpf,fs,PN_length,L);
%%%%%%%%%%%%%%%%%%%%码序列恢复%%%%%%%%%%%%%%%%%%%%%%%
L1=floor(PN_length/2);L2=length(DSSS_BASEBAND);N=PN_length;
%%-----------------非同步情况------------------------%%%%
[gj_t0,gold_code,corrm]=feitongbu_MLE(PN_length,DSSS_BASEBAND,gold_seq); %%%非同步简易最大似然估计法情况下的码恢复
disp('非同步值为:')
gj_t0
disp('错误码元数:')
round((1-corrm)*PN_length)
disp('估计的码序列与真实的扩频码的相关性为:')
corrm
% L3=round(L2/N);
%%---------------同步化过程,同步情况------------------------%%%
% gj_t0=ftb_zkj(DSSS_BASEBAND,PN_length); %%%非同步子空间跟踪法估计非同步值
DSSS_BASEBAND1=DSSS_BASEBAND(N-gj_t0+1:L2-gj_t0); %%%已同步的基带信号,其长度比原有基带信号少一个码周期
% corrm1
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%符号恢复%%%%%%%%%%%%%%%%%%
DSSS_BASEBAND1=[DSSS_BASEBAND1 DSSS_BASEBAND(L2-gj_t0+1:L2) zeros(1,N-gj_t0)]; %%%补充后的基带信号,其长度与原来的一致
L3=round(length(DSSS_BASEBAND1)/N);
symbol_huifu=symbol_recover(DSSS_BASEBAND1,gold_code,L3,PN_length); %%%信息码恢复
figure
subplot(211)
stem(symbol_huifu);
title('恢复出来的信息码')
subplot(212)
stem(symbol)
title('原信息码')
right=length(find(symbol_huifu==symbol))/L;
if right<0.5
right=1-right;
end
up40365.仿真结果
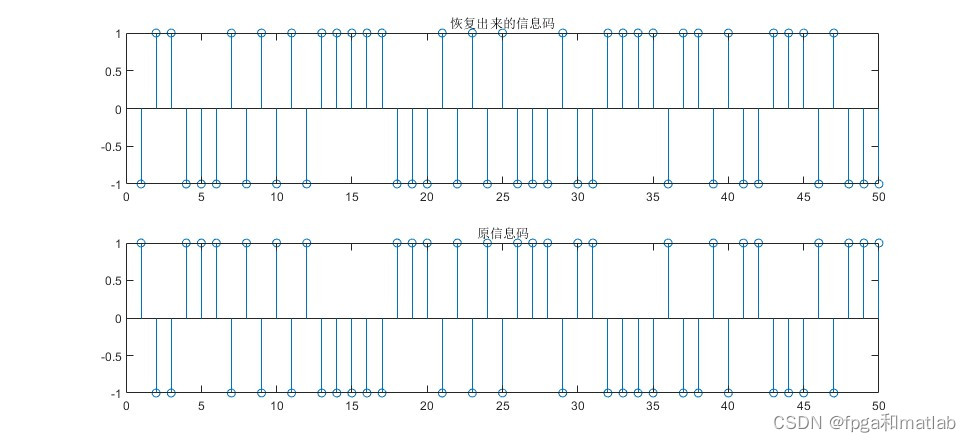
本文详细介绍了基于最大似然估计的BPSK解调系统定时恢复的原理。通过最大化似然函数来估计最佳的采样时刻,可以有效地克服时钟偏差对解调性能的影响。然而,实际通信系统中的定时恢复问题往往更加复杂,需要综合考虑多种因素来选择合适的算法和实现方式。未来的研究可以进一步探索基于最大似然估计的定时恢复算法在复杂信道和多样化调制方式下的应用和优化。





























 7404
7404

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










