【MATLAB例程】维度自适应的EKF代码-从1维~n维，根据状态量和观测量维度自动调整滤波器结构（自动匹配维度）|附代码下载链接

本代码实现了一个扩展卡尔曼滤波（EKF）算法，用于多维非线性系统的状态估计。代码通过动态匹配状态量和观测量的维度（支持任意维度），解决了传统EKF实现中维度固定的局限性。其核心功能是通过融合过程模型与非线性观测模型，优化对系统真实状态的估计，有效降低噪声干扰。

代码介绍

初始化模块

• 动态维度设置：通过变量dim定义状态量和观测量的维度（例如示例中为5维），无需手动调整代码结构，增强了灵活性。
• 噪声与协方差矩阵：定义了过程噪声协方差矩阵Q和观测噪声协方差矩阵R，并生成对应的高斯噪声w和v。
• 状态初始化：真实状态X、未滤波状态X_和EKF估计状态X_ekf均初始化为零矩阵，初始协方差矩阵P0为单位矩阵。

运动模型与观测模型

• 状态更新：假设系统为线性状态转移（X = eye(dim)*X_prev），但观测模型为非线性函数（Z = X.^2 + v），体现了EKF处理非线性观测的能力。
• 未滤波状态模拟：通过叠加过程噪声生成带误差的状态量X_，用于后续滤波效果对比。

EKF算法实现

• 预测步骤：
  • 状态预测：Xpre = X_ekf_prev + w_ekf（含过程噪声）。
  • 观测预测：Z_hat = Xpre.^2，反映非线性观测模型。
  • 雅可比矩阵计算：F（状态转移矩阵，此处为线性单位矩阵）和H（观测矩阵，通过H = diag(2*Xpre)实现非线性观测的线性化）。
  • 协方差传播：PP = F*P*F' + Q。
• 更新步骤：
  • 计算卡尔曼增益Kk，修正状态估计X_ekf和协方差矩阵P，遵循EKF标准流程。

结果可视化与评估

• 时序对比图：绘制各维度真实值、EKF估计值和未滤波值的对比，直观展示滤波效果。
• 误差分析：计算并输出各维度滤波前后的最大绝对误差，并通过累积概率密度曲线（注释部分）进一步量化性能。
• 多维度支持：绘图模块自动适应维度，生成分块子图，便于高维数据分析。

代码特点

1. 灵活性：通过参数dim动态调整状态和观测维度，适用于机器人导航、无人机姿态估计等多维系统。
2. 非线性处理：通过雅可比矩阵线性化观测模型（如H = diag(2*Xpre)），有效解决非线性系统的状态估计问题。
3. 鲁棒性优化：引入过程噪声w_ekf和协方差更新机制，提升算法对动态系统的适应性。
4. 可视化全面：提供时序对比、误差分析及统计指标，支持多维数据的直观评估。

改进方向

• 非线性状态转移：当前状态转移为线性模型，可扩展为通用非线性函数（如f(X)）并计算对应雅可比矩阵。
• 自适应噪声协方差：根据残差动态调整Q和R，提升算法在时变系统中的鲁棒性。
• 代码封装：将EKF核心逻辑封装为函数，支持外部调用和参数配置。

该代码为多维非线性系统的状态估计提供了通用实现框架，结合理论推导与工程实践，适用于学术研究及工程开发场景。通过调整模型参数（如dim、Q、R），可快速适配不同应用需求。

运行结果

1维时的运行结果：

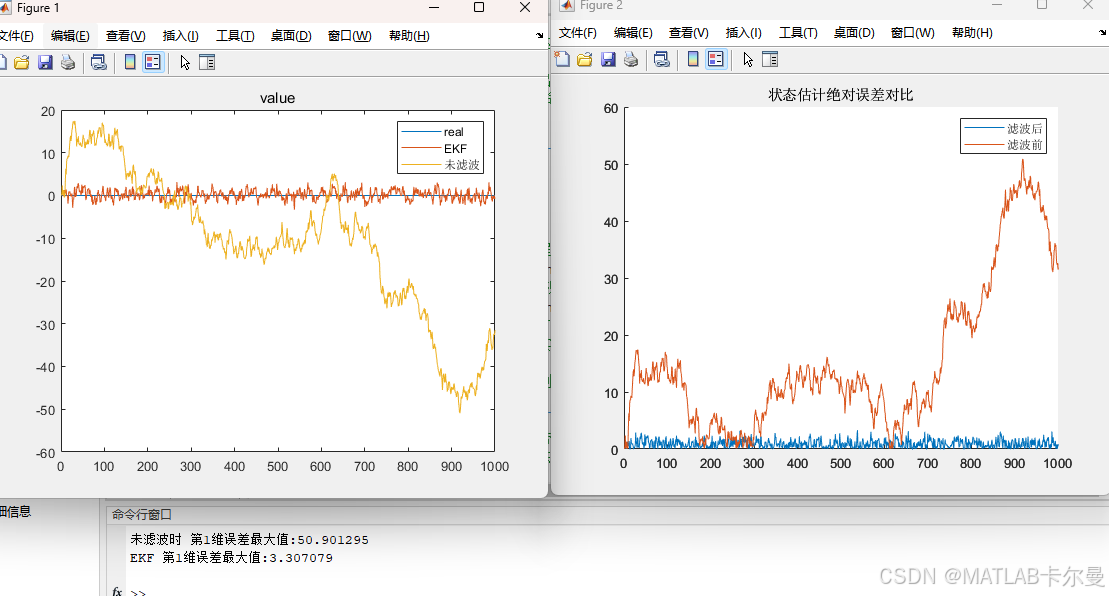
3维时的运行结果：

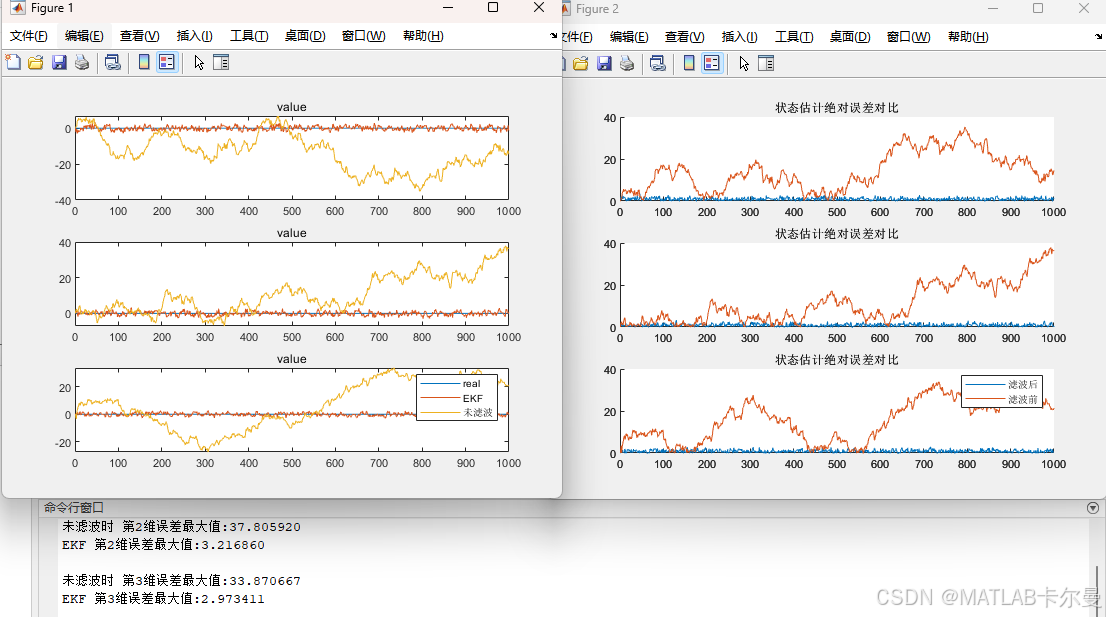
10维时的运行结果：

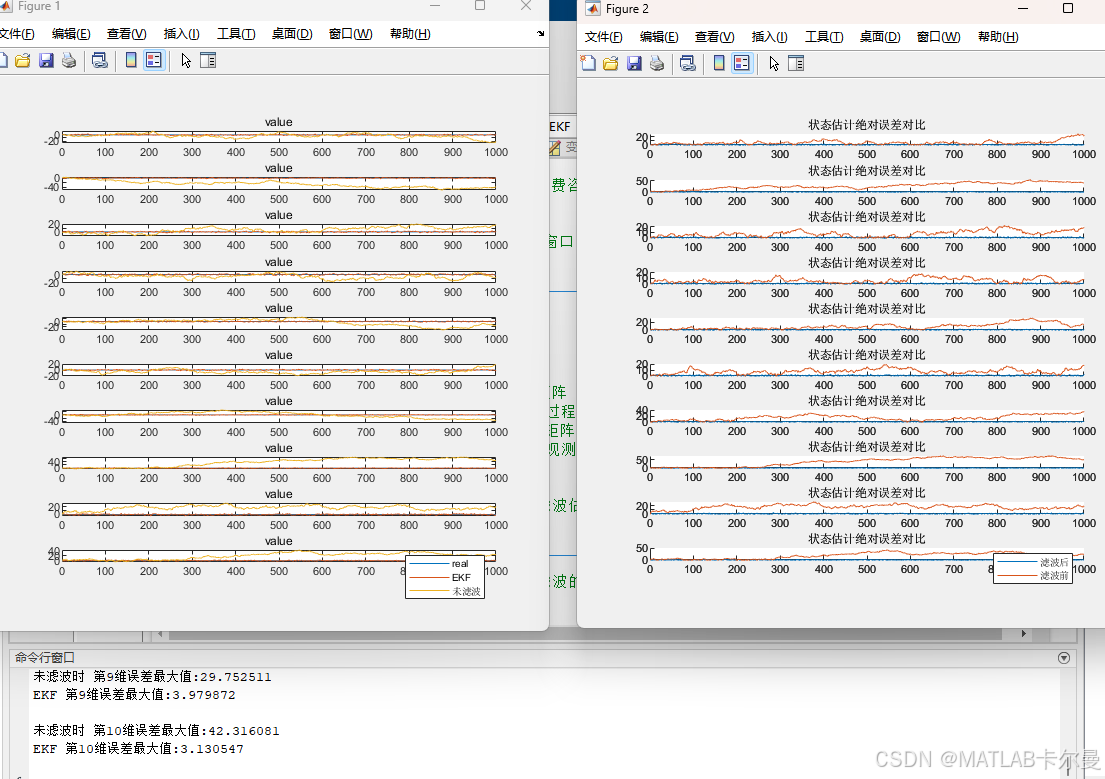
维度调节方法

调节dim变量即可，如下：

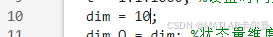
MATLAB源代码

% EKF 自动匹配维度
% 2024-12-26/Ver1
% 2025-01-16/Ver2：修复命令行只输出三维的问题
clear; clc; close all;% 清除变量、命令行和图形窗口
rng(0); % 设置随机数种子

%% 滤波模型初始化
t = 1:1:1000; %设置时间序列
dim = 10;
dim_Q = dim; %状态量维度
dim_R = dim; %观测量维度
Q = 1 * diag(ones(1,dim_Q)); % 过程噪声协方差矩阵
w = sqrt(Q) * randn(size(Q, 1), length(t)); % 过程噪声
R = 10 * diag(ones(1,dim_R)); % 观测噪声协方差矩阵
v = sqrt(R) * randn(size(R, 1), length(t)); % 观测噪声
P0 = 1 * eye(dim_Q); % 初始状态协方差矩阵
X = zeros(dim_Q, length(t)); % 真实状态
X_ekf = zeros(dim_Q, length(t)); % 扩展卡尔曼滤波估计的状态
Z = zeros(dim_R, length(t)); % 观测值形式

完整代码下载链接：https://download.youkuaiyun.com/download/callmeup/90717844

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者