一维模糊自适应EKF的MATLAB代码、模糊规则编辑演示

原创已于 2024-12-13 07:55:23 修改 · 1.4k 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #开发语言

于 2024-12-11 08:23:15 首次发布

卡尔曼专题免费专栏专栏收录该内容

98 篇文章

订阅专栏

在这里插入图片描述

该 MATLAB 代码实现了一维模糊自适应滤波器（FLAEKF），结合了扩展卡尔曼滤波（EKF）和模糊逻辑，以动态调整滤波器的噪声协方差。代码分为多个部分，包括初始化、数据生成、EKF 和模糊自适应 EKF 的实现，最后展示和分析结果。
有关模糊逻辑控制器的介绍，详见：https://blog.youkuaiyun.com/callmeup/article/details/144347186

代码分析与介绍

主要功能

初始化参数：
- 设置采样率和时间序列。
- 初始化系统和观测噪声，模拟噪声变化。
- 初始化状态协方差和状态变量。
数据生成：
- 通过循环生成真实状态值 X 和未滤波的状态值 X_，以及观测值 Z。
扩展卡尔曼滤波（EKF）：
- 通过预测和更新步骤，利用观测值滤波状态。
- 计算状态转移矩阵和观测矩阵，更新状态协方差。
模糊自适应 EKF：
- 根据残差动态调整过程噪声 Q_AEKF 和观测噪声 R_AEKF。
- 使用模糊逻辑系统评估残差，并生成相应的噪声调整。
结果展示：
- 绘制真实值、EKF 输出、模糊自适应 EKF 输出及未滤波值的对比图。
- 计算并输出滤波前后的误差最大值、平均值和标准差。

代码细节

噪声模拟：
- 系统噪声和观测噪声通过正态分布生成，并在特定时间段内引入变化，以模拟真实环境中噪声的动态性。
模糊逻辑：
- 使用已加载的模糊逻辑模型（fuzzy_demo.mat），通过 evalfis 函数评估残差并返回相应的噪声调整值。
结果分析：
- 结果通过图形化展示，直观比较不同滤波方法的性能。
- 误差统计分析提供了对滤波器性能的量化评估。

模糊规则的编写

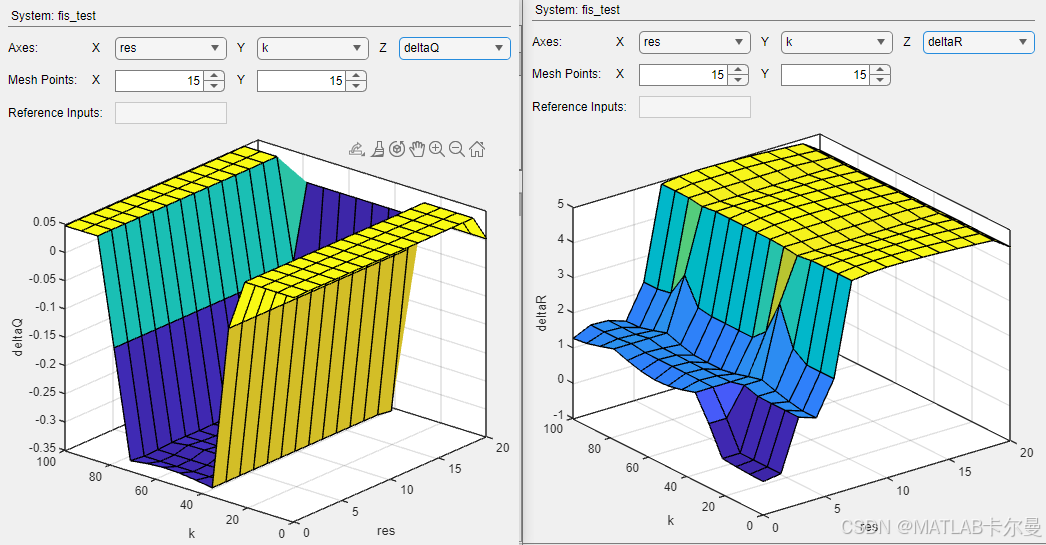
构造的模糊逻辑输入输出为双输入、双输出的形式：
在这里插入图片描述
其中，残差和时序为输入、R和Q的修正值为输出。
模糊规则的图示如下：

程序运行

运行方法

运行操作过程详见下列视频：

EKF下的模糊自适应（一维非线性），MATLAB例程

运行结果

运行结果如下：

状态对比：
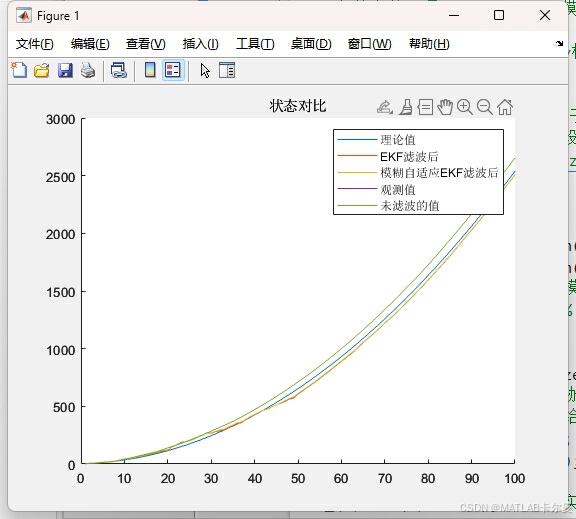
状态误差对比：
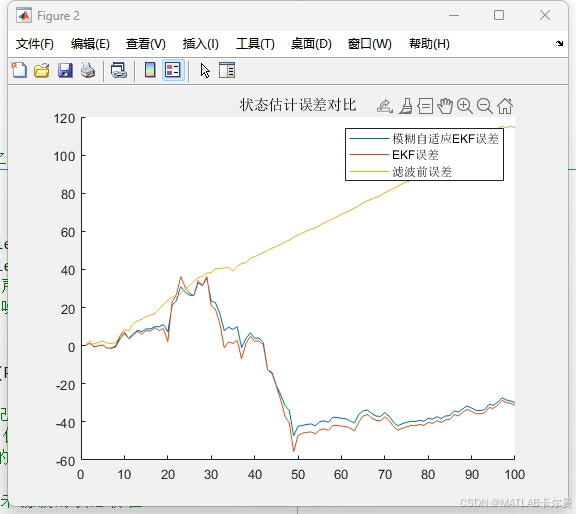
误差输出：

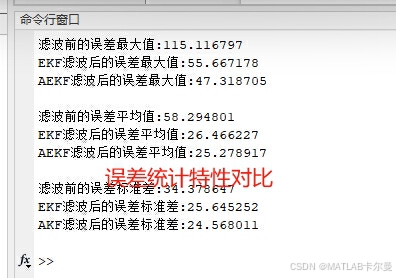
源代码

源代码由m文件、fis文件、存有模糊规则和函数的mat文件三部分构成。

m文件用于运行
mat文件被m文件调用
fis文件在运行时不需要使用，但是如果要修改模糊逻辑控制器，需要使用此文件才能修改

m文件的部分代码如下：

% 模糊自适应滤波（一维FLAEKF）
% 文件名的FL是fuzzy logic，模糊逻辑
% 2024-12-08/Ver1
% 2024-12-09/Ver2：使用fuzzy模块

clc; clear; close all;
rng(0); % 设置固定的随机数种子
load fuzzy_demo.mat %导入已设置好的模糊逻辑
% 如果需要调节，需要使用 fuzzy (2015b版本及之前的版本) 或 fuzzyLogicDesigner 打开fis文件修改、导入和保存
%% 初始化
T = 1; % 设置采样率
t = T:T:100; % 构建时间序列
Q0 = 1; w = sqrt(Q0) * randn(size(Q0, 1), length(t)); % 系统噪声
R0 = 1; v = sqrt(R0) * randn(size(R0, 1), length(t)); % 观测噪声
v(20:50) = 5 * v(20:50); % 模拟变化的观测噪声
w(40:80) = 0.2 * w(40:80); % 模拟变化的系统噪声

P0 = 1; % 状态协方差
P_num = zeros(length(t), size(P0, 1), size(P0, 2)); % 存放每次迭代的P
P_num(1, :, :) = P0; % 记录协方差
X = zeros(1, length(t)); % 给状态真实值X分配空间
X_ekf = zeros(1, length(t)); % 储存滤波后的值
X_aekf = zeros(1, length(t)); % 储存滤波后的值
X(1) = 3; % 初始状态值
X_(1) = X(1) + w(1); % 由真实值加上误差生成未滤波的状态初值

%% 生成数据
for i1 = 2:length(t)
    X(i1) = X(i1-1)^0.5 + X(i1-1); % 真实值生成
    X_(i1) = X_(i1-1)^0.5 + X_(i1-1) + w(i1); % 未滤波的状态生成
    Z(i1) = X(i1)^0.5 + v(i1); % 观测量生成
end