距离与AoA辅助的三维定位方法，可自定义基站数量，MATLAB代码交流

本MATLAB代码实现了一个基于距离与到达角（AoA）的三维测距系统，主要用于在动态环境中估计目标物体的位置。提供本算法与仅侧角（AoA）的定位误差对比

代码运行结果

定位结果如下：

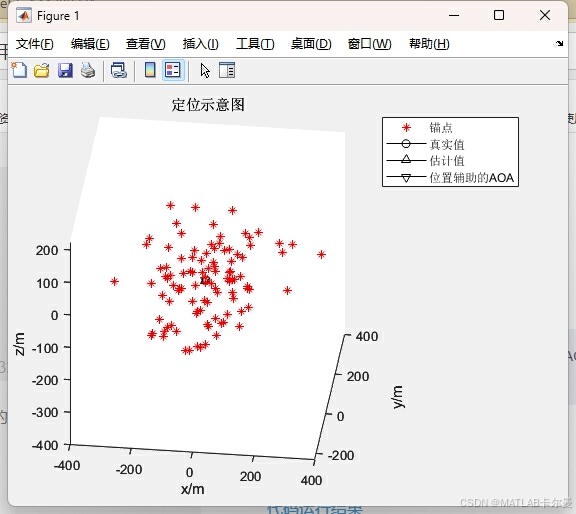
命令行的坐标和误差输出：

部分代码截图：

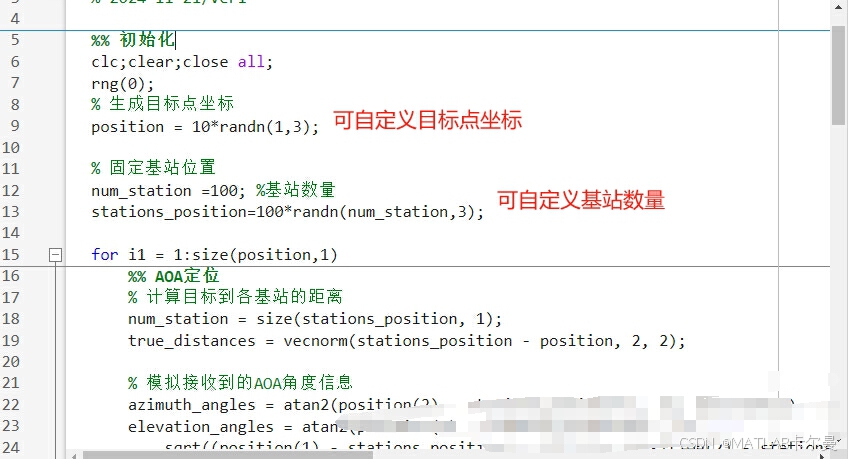
源代码

部分源代码如下：

% 距离与AOA辅助的三维测距，自适应基站数量
% 2024-11-21/Ver1

%% 初始化
clc;clear;close all;
rng(0);
% 生成目标点坐标
position = 10*randn(1,3);

% 固定基站位置
num_station =100; %基站数量
stations_position=100*randn(num_station,3);

for i1 = 1:size(position,1)
    %% AOA定位
    % 计算目标到各基站的距离
    num_station = size(stations_position, 1);
    true_distances = vecnorm(stations_position - position, 2, 2);
    
    % 模拟接收到的AOA角度信息
    azimuth_angles = atan2(position(2) - stations_position(:, 2), position(1) - stations_position(:, 1));
    elevation_angles = atan2(position(3) - stations_position(:, 3), ...
        sqrt((position(1) - stations_position(:, 1)).^2 + (position(2) - stations_position(:, 2)).^2));
    
    % 假设测量的AOA角度和距离上加一些噪声
    AOA_noise = 1e-1; % AOA 角度噪声
    distance_noise = 1; %辅助AOA的距离噪声
    azimuth_angles = azimuth_angles + AOA_noise * randn(num_station, 1);
    elevation_angles = elevation_angles + AOA_noise * randn(num_station, 1);
    distances = true_distances  + distance_noise * randn(num_station, 1);
    % 使用最小二乘法进行定位估计
    % 定义目标位置的初始猜测
    A = zeros(num_station , 3); % 2 行 per anchor, 4 列 (x, y, z, 1)
    b = zeros(num_station , 1);

代码功能概述

• 目标：在三维空间中通过固定基站的位置和目标点的位置，结合到达角（AOA）和距离信息，进行目标位置的估计。
• 方法：使用最小二乘法来估计目标位置，并比较普通AoA方法下的估计效果。

主要步骤分析

初始化部分

• clc; clear; close all;：清空命令行、变量和关闭所有图形窗口。
• rng(0);：设置随机数生成器的种子，以确保结果可重复。
• 生成目标点坐标：在三维空间中随机生成一个目标点的位置。
• 固定基站位置：生成多个随机位置的基站。

AOA定位

1. 计算真实距离：使用 vecnorm 函数计算目标与各基站之间的真实距离。

2. 模拟AOA角度信息：

   • 计算目标相对于基站的方位角（azimuth）和俯仰角（elevation）。
   • 为模拟的角度和距离添加噪声，以模拟实际测量中的不确定性。

3. 构建线性方程：

   • 初始化矩阵 A 和向量 b，用以存储线性方程组的数据。
   • 对每个基站，计算单位向量，并构建线性方程。

4. 最小二乘法求解：

   • 使用最小二乘法估计目标位置，分别计算不带距离辅助和带距离辅助的AOA估计。

绘图与输出

• 通过 plot3 函数绘制基站位置、真实目标位置和估计位置，以可视化估计效果。
• 输出真实位置、估计位置及其误差，便于分析定位精度。

总结

总体而言，这段代码展示了一种有效的三维定位方法，通过结合距离和AOA信息，利用噪声模型进行数据模拟，并通过最小二乘法进行位置估计。它为研究和开发更复杂的定位算法提供了基础，可以在实际应用中进行进一步优化和扩展。

如有需要，可通过下方卡片联系作者（代码咨询、定制等）