3-PRRS并联机械手几何与逆运动学

3‐PRRS型并联机械手的几何结构 与逆运动学

1 引言

与六支链并联机构相比，具有六自由度和三支链或三脚架机构的并联机构具有较大的工作空间和较简单的奇异构型。已知的三脚架机构包括URS [1], ESR [2], RRPS [3], RES [4–6], PPSP [7], PRPS [8], CRS [9], CCC [10]。

本文提出了确定3‐PRRS型六自由度三脚架机构几何结构并求解其逆运动学的方法。根据并联机构的构型原理[11]，所研究的并联机构通过三个零自由度的PRRS型被动闭合运动链将动平台与固定基座连接而成。为了描述该并联机构的几何结构并研究其运动学特性，采用两个固定在每个运动副两个构件上的笛卡尔坐标系UVW和XYZ[12]。这些坐标系的W轴和Z轴沿运动副构件旋转和平移运动的轴线方向，U轴和X轴则沿从W轴到Z轴所作垂线t的方向。

坐标系Uj VjWj和XkYkZk之间的变换矩阵具有如下形式

$$
T_{jk} =
\begin{bmatrix}
c_\gamma c_\beta & -s_\gamma c_\alpha + c_\gamma s_\beta s_\alpha & s_\gamma s_\alpha + c_\gamma s_\beta c_\alpha & a_{jk} \
s_\gamma c_\beta & c_\gamma c_\alpha + s_\gamma s_\beta s_\alpha & -c_\gamma s_\alpha + s_\gamma s_\beta c_\alpha & b_{jk} \
-s_\beta & c_\beta s_\alpha & c_\beta c_\alpha & c_{jk} \
0 & 0 & 0 & 1
\end{bmatrix}
$$

其中，$a_{jk}$：沿Wj与Zk轴之间公垂线tjk的正方向测量的两轴之间的距离；$\alpha_{jk}$：根据右手定则，绕tjk的正方向测量的Wj与Zk轴正方向之间的夹角；$b_{jk}$：沿Zk轴正方向从tjk方向到Xk轴方向的距离；$\beta_{jk}$：根据右手定则，测量的tjk与Xk轴正方向之间的夹角；$c_{jk}$：沿Wj轴正方向从Uj轴正方向到tjk方向的距离；$\gamma_{jk}$：根据右手定则，测量的Uj轴与tjk正方向之间的夹角。

具有上述形式的二元连杆两端固定坐标系之间的变换矩阵包含常数参数，称为二元连杆矩阵。运动副两个构件上固定坐标系之间的变换矩阵称为运动副矩阵，其中包含表征运动副构件相对位置的可变参数。

2 并联机构的几何结构

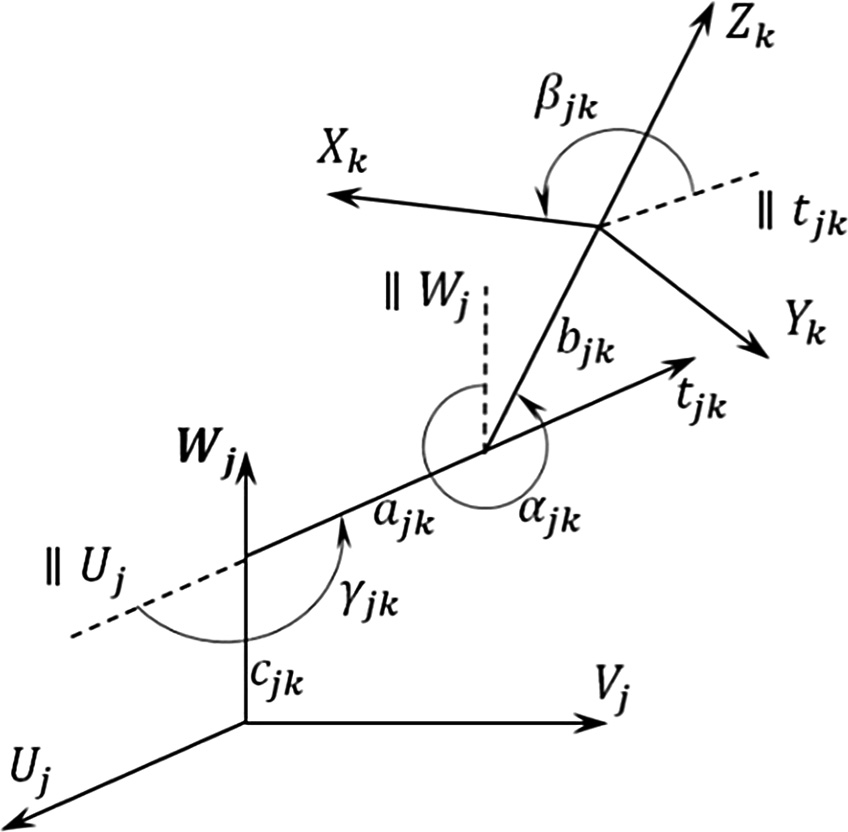
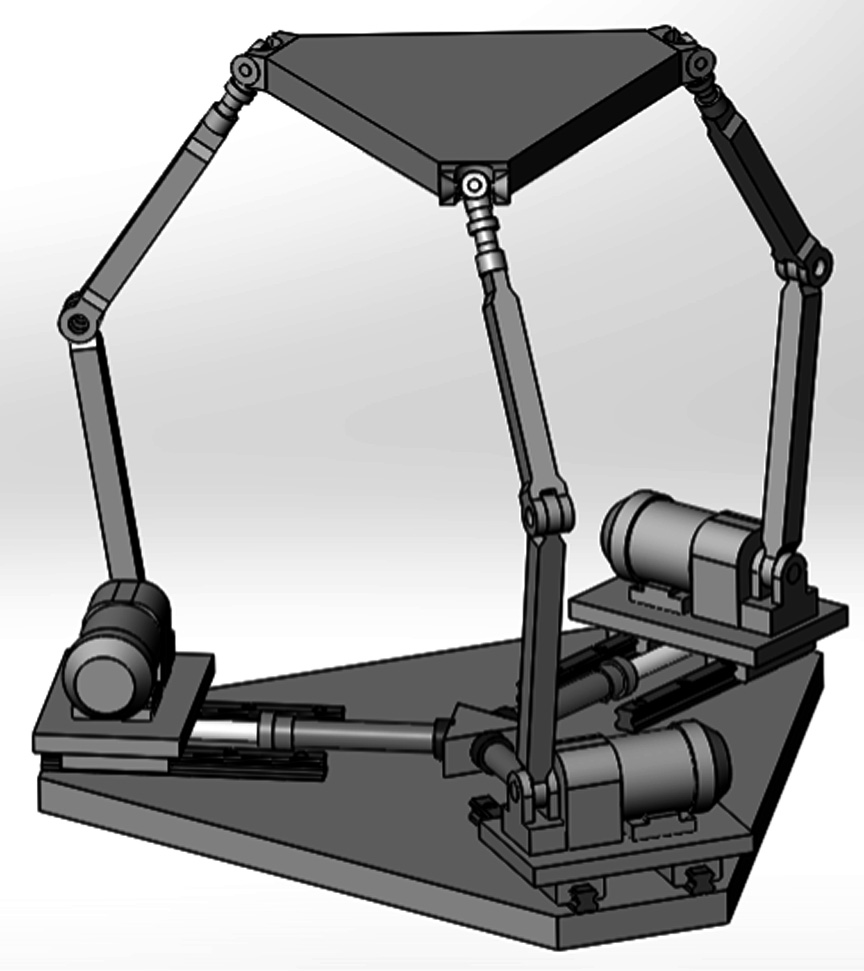
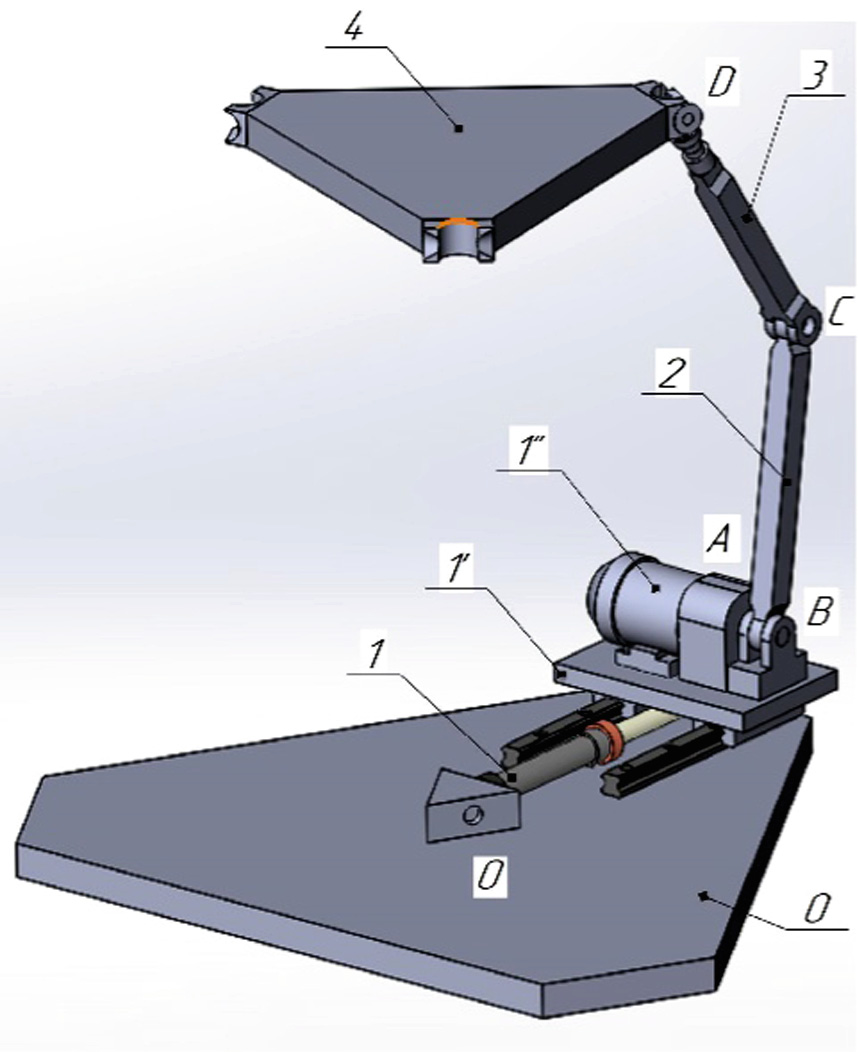
图2显示了该并联机构的三维模型，其中动平台4通过三条相同的PRRS型支链与固定基座0相连。考虑该并联机构的一条支链OABCD（图3），其中液压缸的活塞杆与安装有电机10的移动滑块100（电机带有齿轮箱）一起相对于固定基座0作平移运动，形成移动运动副A。连杆2通过转动运动副B与齿轮箱的轴连接，并通过转动运动副C与连杆3连接。连杆3通过球面运动副D与动平台4连接。

液压缸活塞杆和齿轮箱轴为输入连杆，运动副A和B为主动运动副。

将绝对坐标系U0V0W0与固定基座连接，并将坐标系XPYPZP与动平台连接，其中W0轴和ZP轴分别垂直于固定基座和动平台的平面。坐标系UjVjWj和XkYkZk固定在运动副的构件上，其中j; k = 1; 2; 3; 4：此处运动副A、B、C、D用数字1、2、3、4分别表示。由图4可以看出，连杆1、2、3以及运动副A、B、C的矩阵具有以下元素：

• $T_{01} = T_{01}(0, a_{01}, 0, 0, c_{01}, \gamma_{01})$
• $PP_1 = PP_1(0, 0, 0, 0, c_1, 0)$
• $T_{12} = T_{12}(a_{12}, \alpha_{12}, b_{12}, \beta_{12}, 0, 0)$
• $PR_2 = PR_2(0, 0, 0, b_{22}, 0, 0)$
• $T_{23} = T_{23}(a_{23}, 0, 0, 0, 0, 0)$
• $PR_3 = PR_3(0, 0, 0, b_{33}, 0, 0)$
• $T_{34} = T_{34}(a_{34}, 0, 0, 0, 0, 0)$

其中，

• $a_{01} = 900$
• $c_{01} = OO_1$
• $c_1 = O_1O’_1 = s_1$
• $a_{12} = O’_1O_2$
• $\alpha_{12} = -90^\circ$
• $b_{12} = O_2O’_2$
• $\beta_{12} = 90^\circ$
• $b_{22} = h_2$
• $a_{23} = O_2O_3$
• $b_{33} = h_3$
• $a_{34} = O’_3O_4$

其中，参数$a_{01}$；$c_{01}$；$\gamma_{01}$；$a_{12}$；$\alpha_{12}$；$b_{12}$；$\beta_{12}$；$a_{23}$；$a_{34}$为常数，用于表征支链的几何结构，而参数$c_1 = s_1$和$b_{22} = h_2$为变量，用于表征运动副各元件之间的相对运动，其中可变参数$s_1$和$h_2$为输入参数，$h_3$为输出参数。

所讨论的并联机构其余两条支链具有类似的参数。

3 并联机构的逆运动学

固定在动平台4上的坐标系XP YPZP相对于绝对坐标系U0 V0W0的位置由变换矩阵T04确定，该变换矩阵具有以下常数参数$T_{04} = T_{04}(a_{04}, \alpha_{04}, b_{04}, \beta_{04}, c_{04}, \gamma_{04})$，如图4所示。已知坐标系XPYP ZP的位置，需要确定输入的可变参数$s_1$和$h_2$。球面副中心D的坐标可以通过坐标系XP YPZP确定

$$
[U_D, V_D, W_D]^T = T_{0P} \cdot T_{P4} \cdot [1, 0, 0, 0]^T \tag{2}
$$

从图4可以看出，矩阵$T_{P4}$具有以下常数参数$T_{P4} = T_{P4}(a_{P4}, 0, 0, 0, c_{P4}, \gamma_{P4})$；其中$a_{P4} = O_P D$, $c_{P4} = P O_P$。点D的坐标也可以通过支链OABCD确定

$$
[U_D, V_D, W_D]^T = T_{01} \cdot PP_1 \cdot T_{12} \cdot PR_2 \cdot T_{23} \cdot PR_3 \cdot T_{34} \cdot [1, 0, 0, 0]^T \tag{3}
$$

令公式(2)和(3)的右侧相等，得到

$$
\begin{cases}
-b_{12}\cos c_{01} + s_1\sin c_{01} - a_{23}\sin c_{01}\sin h_2 - a_{34}\sin c_{01}\sin(h_2 + h_3) = U_D \
-b_{12}\sin c_{01} - s_1\cos c_{01} + a_{23}\cos c_{01}\sin h_2 + a_{34}\cos c_{01}\sin(h_2 + h_3) = V_D \
c_{01} + a_{12} + a_{23}\cos h_2 + a_{34}\cos(h_2 + h_3) = W_D
\end{cases} \tag{4}
$$

其中$U_D$；$V_D$；$W_D$为已知值，由矩阵$T_{0P}$和$T_{P4}$在公式(2)中的元素确定。

对方程组（4）的分析表明，前两个方程是线性相关的。因此，参数$s_1$、$h_2$和$h_3$中有一个可以作为自由参数选择。事实上，从图4可以看出，动平台4上点D的位置在液压缸1的活塞杆处于不同位置时保持不变，即$s_1$是一个自由参数。其取值区间需满足条件$l_{O_2D}^{\text{max}} \leq a_{23} + a_{34}$。

在变换方程组(4)的第一和第三个方程以及以下符号之后

$$
K = \frac{U_D + b_{12} \cos c_{01}}{\sin c_{01}}, \quad M = W_D - c_{01} - a_{12}
$$

产生

$$
E \cdot \sin^2 h_2 - F \cdot \sin h_2 + G = 0 \tag{5}
$$

其中

$$
\begin{aligned}
E &= (s_1 - K)^2 + M^2 \
F &= 2 \cdot (a_{23} + a_{34} \cdot \cos h_3) \cdot (s_1 - K) \
G &= (a_{23} + a_{34} \cdot \cos h_3)^2 - M^2 \
\cos h_3 &= \frac{(s_1 - K)^2 + M^2 - a_{23}^2 - a_{34}^2}{2 \cdot a_{23} \cdot a_{34}}
\end{aligned}
$$

由公式(5)可得

$$
h_2 = \arcsin\left( \frac{F \pm \sqrt{F^2 - 4EG}}{2E} \right) \tag{6}
$$

对应于二连杆机构BCD的两个解。

4 结论

3‐PRRS型并联机构通过三条具有零自由度的PRRS型被动闭链运动链（CKC）将动平台与固定基座连接而成。这些被动闭链运动链不对动平台的运动施加几何约束，从而保留了其6个自由度。为了描述该并联机构的几何结构并研究其运动学特性，采用在每个运动副的两个构件上分别固定一个笛卡尔坐标系的方法。

这些坐标系之间的变换矩阵包含六个参数，可用于完整表征该并联机构的几何结构。事实上，空间中刚体的位置由六个独立参数确定。固定在二元连杆末端的坐标系的变换矩阵具有常数参数，称为二元连杆矩阵；固定在运动副两个构件上的坐标系之间的变换矩阵称为运动副矩阵，其中包含表征运动副构件相对位置的可变参数。文中确定了3‐PRRS型并联机构的常数参数和可变参数。基于支链的闭环矩阵方程求解该并联机构的逆运动学问题。分析结果表明，输入棱柱副的可变参数是自由的。