【AI概念】协方差（covariance）与相关系数（correlation）是什麽？有什么区别？在机器学习中担任什么角色？|协方差矩阵、马氏距离、归一化|主成分分析PCA、代码实现与可视化、实际应用

人工智能AI酱

于 2025-06-22 18:16:22 发布

阅读量888

点赞数 28

CC 4.0 BY-SA版权

分类专栏：【AI概念】专栏系列文章标签：人工智能机器学习 python 协方差相关系数协方差矩阵 ai

本文链接：https://blog.youkuaiyun.com/ai_aijiang/article/details/148829993

【AI概念】专栏系列专栏收录该内容

25 篇文章

订阅专栏

大家好，我是爱酱。本篇將會系统讲解协方差（covariance，又称共变异数）与相关系数（correlation coefficient，或简称correlation）的定义、公式、几何意义、实际案例和应用场景。内容适合初学者和进阶读者，分步解释，配合公式和可视化示例。

注：本文章含大量数学算式、详细例子说明及大量代码演示，大量干货，建议先收藏再慢慢观看理解。新频道发展不易，你们的每个赞、收藏跟转发都是我继续分享的动力！

一、协方差（Covariance）与相关系数（Correlation）简单介紹

名称定义

协方差：同時亦被称為“共变异数”，英文为covariance，常用符号为 $\mathrm{cov}(X, Y)$ 或 $\sigma(X, Y)$ 。
相关系数：常被称为“相关系数”，英文为correlation coefficient，简称 correlation，常用符号为 $r$ 或 $\rho$ 。

协方差与相关系数在机器学习中的作用

要学习这两概念，最好先了解他们在机器学习中担任什么样的角色，有什么用途。

特征关系分析与特征选择
- 协方差和相关系数用于衡量特征之间的线性关系。
- 在特征选择阶段，相关系数常用于筛除高度相关（冗余）的特征，减少多重共线性，提高模型泛化能力。例如，若两个特征相关系数 $r > 0.9$ ，通常只保留一个。
降维与特征提取
- 主成分分析（PCA）等降维算法核心就是对协方差矩阵（Covariance Matrix）做特征值分解，找到数据方差最大的方向，实现信息压缩和特征提取。
  爱酱之前也做过主成分分析（PCA）的深入介绍文章，有兴趣的同学可以去看看！
  主成分分析（PCA）文章传送门：
  【AI深究】主成分分析（PCA）全网最详细全流程详解与案例（附大量Python代码演示）|数学原理、案例流程、代码演示及结果解读|几何意义与主成分选择、与LDA的对比、实际应用场景、工程建议与优缺点-优快云博客
- 协方差矩阵的特征向量即为主成分方向，特征值表示该方向上的方差大小。
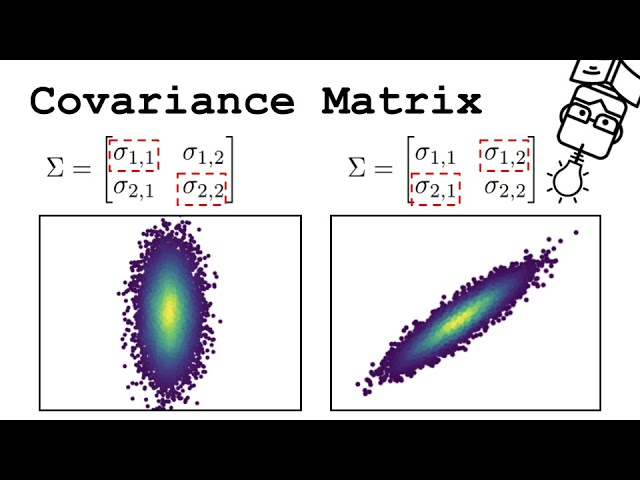
异常检测与数据探索
- 通过分析协方差和相关系数，可以发现异常点或异常关系，辅助异常检测、数据清洗等。
- 例如，利用协方差矩阵计算马氏距离（Mahalanobis Distance），可检测多变量异常点。
回归与建模
- 在线性回归中，协方差用于衡量自变量与因变量的线性关系强度，相关系数越高，线性模型拟合效果通常越好。
- 在高维数据建模时，相关系数也用于判断特征之间的独立性，防止模型过拟合。
深度学习中的应用
- 在卷积神经网络（CNN）、循环神经网络（RNN）等结构中，协方差和相关性用于捕捉空间或时序特征间的依赖关系。
- 注意力机制（Attention）本质上也是对相关性的一种建模。
简单例子
- 特征选择：假设有两个特征“身高”和“腿长”，相关系数高达0.95，说明它们高度冗余，建模时可以只保留一个。
- PCA降维：用协方差矩阵分解得到的主成分，可以将高维图像数据压缩到低维，提升计算效率和可视化效果。
- 异常检测：利用协方差矩阵和马氏距离，可以发现与其他样本差异极大的异常点。

二、协方差的定义与直观意义

1. 协方差的数学定义

协方差衡量两个随机变量之间的线性相关程度，定义如下：

$E[X]$ 、 $E[Y]$ 分别是 $X$ 和 $Y$ 的期望值（均值）。
如果是样本协方差，常用无偏估计：

2. 协方差的几何/统计意义

正协方差： $X$ 大于均值时 $Y$ 也倾向于大于均值， $X$ 和 $Y$ 同向变化（正相关）（Possitive Correlation）。
负协方差： $X$ 大于均值时 $Y$ 倾向于小于均值， $X$ 和 $Y$ 反向变化（负相关）（Negative Correlation）。
协方差为零： $X$ 和 $Y$ 之间没有线性关系（不相关）。

协方差值的大小受变量单位和尺度影响，不便于直接比较不同变量间的相关性。

三、相关系数的定义与归一化

1. 相关系数的数学定义

相关系数是对协方差的归一化（Normalization）处理，消除了单位影响，取值范围为 $[-1, 1]$ ：

$\sigma_X$ 、 $\sigma_Y$ 分别为 $X$ 和 $Y$ 的标准差。
$r_{XY}=1$ 表示完全正相关， $r_{XY}=-1$ 表示完全负相关， $r_{XY}=0$ 表示不相关。

2. 相关系数的几何意义

相关系数实际上等价于两个中心化向量的余弦相似度（cosine similarity）：
反映了两个变量的“方向一致性”，与变量的绝对大小无关。

四、实际案例与可视化

1. 案例说明

假设有甲、乙两人对6本书的评分如下：

	A	B	C	D	E	F
甲	4	3	3	0	5	3
乙	4	2	4	0	4	4

甲的评分向量 $\vec{x} = (4,3,3,0,5,3)$
乙的评分向量 $\vec{y} = (4,2,4,0,4,4)$

协方差计算：

五、协方差矩阵与多变量相关性

1. 协方差矩阵的定义

对于 $d$ 维特征的多变量数据，协方差矩阵（Covariance Matrix）是一个 $d \times d$ 的对称矩阵，定义如下：

对角线元素是各变量的方差，非对角线元素是变量间的协方差。

2. 协方差矩阵的意义

协方差矩阵描述了多维数据各特征之间的线性相关性结构。
在PCA（主成分分析）等算法中，协方差矩阵的特征向量就是主成分方向，特征值表示这些方向上的方差大小。

六、Python代码实现与可视化

1. 协方差与相关系数的计算

import numpy as np

# 甲、乙评分
x = np.array([4, 3, 3, 0, 5, 3])
y = np.array([4, 2, 4, 0, 4, 4])

# 协方差
cov = np.cov(x, y, ddof=1)[0, 1]
print("协方差:", cov)

# 相关系数
corr = np.corrcoef(x, y)[0, 1]
print("相关系数:", corr)

2. 协方差矩阵的计算与可视化

假设有三维特征数据：

import matplotlib.pyplot as plt
import numpy as np

# 甲、乙评分
x = np.array([4, 3, 3, 0, 5, 3])
y = np.array([4, 2, 4, 0, 4, 4])

# 协方差
cov = np.cov(x, y, ddof=1)[0, 1]
print("协方差:", cov)

# 相关系数
corr = np.corrcoef(x, y)[0, 1]
print("相关系数:", corr)

# 三维数据
data = np.array([
    [4, 3, 5],
    [3, 2, 4],
    [3, 4, 3],
    [0, 0, 2],
    [5, 4, 5],
    [3, 4, 4]
])
# 协方差矩阵
cov_matrix = np.cov(data.T)
print("协方差矩阵:\n", cov_matrix)

# 可视化热力图
plt.imshow(cov_matrix, cmap='coolwarm', interpolation='nearest')
plt.colorbar()
plt.title("Covariance Matrix Heatmap")
plt.xlabel("Feature")
plt.ylabel("Feature")
plt.show()