【AI深究】朴素贝叶斯（Naive Bayes）全网最详细全流程详解与案例（附大量Python代码演示）| 数学原理、案例流程、代码演示及结果解读 | 工程启示、如何用真实数据集做类似可视化？

人工智能AI酱

于 2025-06-21 03:28:36 发布

阅读量857

点赞数 17

CC 4.0 BY-SA版权

分类专栏：【AI深究】专栏系列文章标签：人工智能 python 机器学习朴素贝叶斯 ai Naive Bayes PCA

本文链接：https://blog.youkuaiyun.com/ai_aijiang/article/details/148802726

【AI深究】专栏系列专栏收录该内容

36 篇文章

订阅专栏

大家好，我是爱酱。本篇将会系统讲解朴素贝叶斯（Naive Bayes）的原理、公式推导、案例流程、代码实现与工程建议。内容适合初学者和进阶读者，分步解释，配合公式和具体例子。

注：本文章含大量数学算式、详细例子说明及大量代码演示，大量干货，建议先收藏再慢慢观看理解。新频道发展不易，你们的每个赞、收藏跟转发都是我继续分享的动力！

一、朴素贝叶斯简介

朴素贝叶斯（Naive Bayes）是一类基于贝叶斯定理与特征条件独立假设的概率分类算法。它以简单、高效、易于实现著称，广泛应用于文本分类、垃圾邮件过滤、情感分析等领域。

核心思想：假设各特征之间相互独立，通过贝叶斯定理计算后验概率，选择概率最大的类别作为预测结果。
常见类型：高斯朴素贝叶斯、伯努利朴素贝叶斯、多项式朴素贝叶斯。

二、朴素贝叶斯的数学原理

1. 贝叶斯定理

朴素贝叶斯的基础是贝叶斯定理：

相信大多数都对这公式都不陌生，因为高中应该都学过。但应用在机器学习的时候，他代表的东西就有一点变化了。

其中：

$y$ ：类别标签
$x$ ：特征向量
$P(y|x)$ ：在已知 $x$ 时属于类别 $y$ 的后验概率
$P(x|y)$ ：在类别 $y$ 下观测到 $x$ 的概率（似然）
$P(y)$ ：类别 $y$ 的先验概率
$P(x)$ ：观测到 $x$ 的概率（归一化常数）

2. 条件独立假设

朴素贝叶斯假设各特征在类别已知的情况下相互独立，即：

这样极大地简化了多特征联合概率的计算。

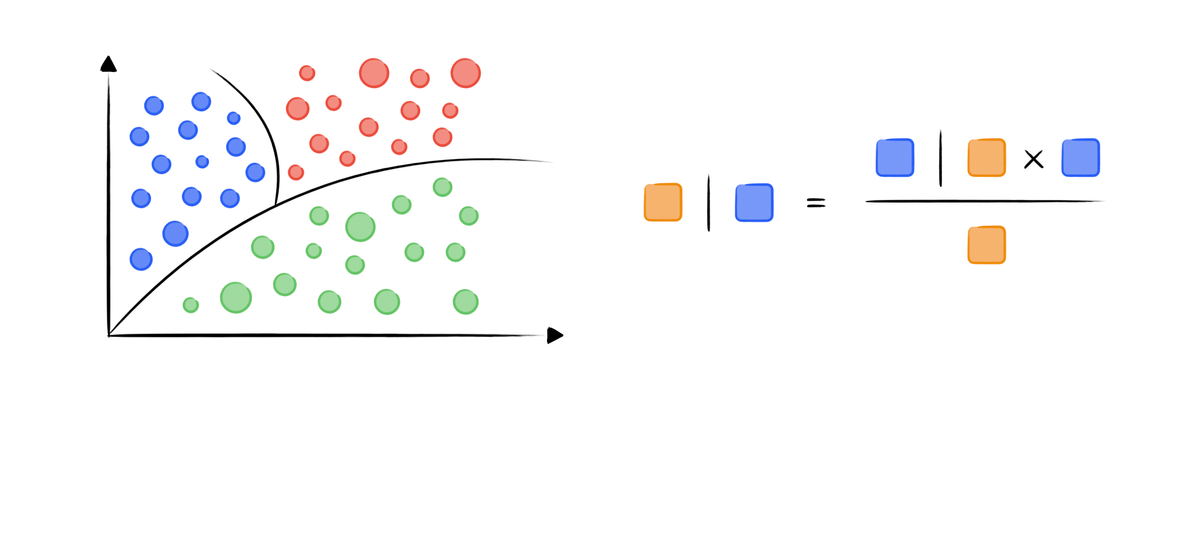
3. 分类决策规则

对于给定样本 $x$ ，预测类别为：

通常用对数化简为：

三、朴素贝叶斯案例流程

Step 1：准备数据

收集特征和类别标签，常见于文本、二值、计数等数据。
可选：对文本数据进行分词、向量化等预处理。

Step 2：计算先验概率

统计每个类别在训练集中的频率，得到 $P(y)$ 。

Step 3：计算条件概率

对每个特征 $x_i$ 和类别 $y$ ，统计 $P(x_i|y)$ 。
不同类型的朴素贝叶斯有不同的条件概率建模方法（见下文）。

Step 4：预测新样本

对于新样本 $x$ ，用上述公式计算每个类别的后验概率。
选择概率最大的类别作为预测结果。

Step 5：模型评估

用测试集评估准确率、混淆矩阵等指标。
可绘制ROC曲线、学习曲线等。

四、朴素贝叶斯代码演示（文本分类案例）

import numpy as np
import matplotlib.pyplot as plt
from sklearn.naive_bayes import MultinomialNB
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.decomposition import PCA

# 1. Create a synthetic, clearly separable dataset
positive_words = ["good", "excellent", "fantastic", "amazing", "wonderful", "love", "great", "awesome", "nice", "pleasant"]
negative_words = ["bad", "terrible", "awful", "horrible", "hate", "worst", "boring", "poor", "dull", "disappointing"]

np.random.seed(0)

# 20 positive and 20 negative samples
texts = []
labels = []
for _ in range(20):
    sample = " ".join(np.random.choice(positive_words, size=3, replace=True))
    texts.append(sample)
    labels.append(1)
for _ in range(20):
    sample = " ".join(np.random.choice(negative_words, size=3, replace=True))
    texts.append(sample)
    labels.append(0)

# 2. Vectorize
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(texts)

# 3. Train Naive Bayes
nb = MultinomialNB()
nb.fit(X, labels)

# 4. Prepare test samples
test_texts = [
    "good excellent fantastic",   # positive
    "bad terrible awful",         # negative
    "amazing wonderful love",     # positive
    "boring dull disappointing",  # negative
    "awesome awesome bad",        # mixed
    "worst pleasant horrible",    # mixed
]
X_test = vectorizer.transform(test_texts)
y_pred = nb.predict(X_test)

# 5. Project to 2D for visualization
pca = PCA(n_components=2, random_state=42)
X_all = np.vstack([X.toarray(), X_test.toarray()])
X_all_2d = pca.fit_transform(X_all)
X_2d = X_all_2d[:len(X.toarray())]
X_test_2d = X_all_2d[len(X.toarray()):]

# 6. Plot training data
plt.figure(figsize=(8, 6))
colors = ['red' if label == 1 else 'blue' for label in labels]
plt.scatter(X_2d[:, 0], X_2d[:, 1], c=colors, alpha=0.6, label='Training data')

# 7. Plot test data
test_colors = ['green' if pred == 1 else 'purple' for pred in y_pred]
plt.scatter(X_test_2d[:, 0], X_test_2d[:, 1], c=test_colors, marker='*', s=200, edgecolor='k', label='Test data')
for i, txt in enumerate(test_texts):
    plt.annotate(f"{txt}\n(pred={y_pred[i]})", (X_test_2d[i, 0]+0.2, X_test_2d[i, 1]), fontsize=8, color=test_colors[i])

plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.title('Naive Bayes Text Classification Visualization (Synthetic Data)')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

# 8. Output predictions
for text, pred in zip(test_texts, y_pred):
    print(f'"{text}": predicted class {pred}')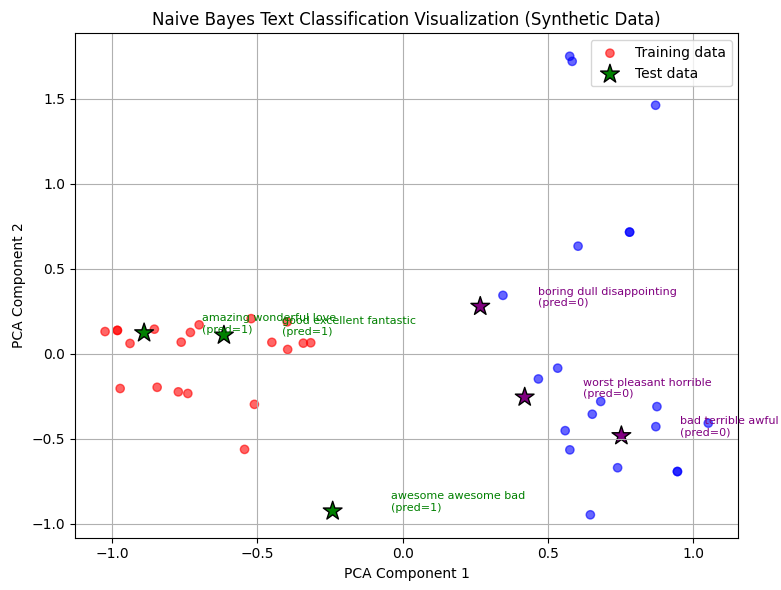

五、代码流程与结果解读

这段代码演示了一个清晰且合成的文本分类示例，结合了多项式朴素贝叶斯算法和PCA降维可视化，具体解释如下：

数据构造：
- 定义了两组词汇：正面情感词和负面情感词。
- 通过随机从每组词汇中选取3个词，生成了20个正面样本和20个负面样本，确保数据类别明显可分。
文本向量化：
- 使用CountVectorizer将文本转换为高维稀疏的词频矩阵，适合朴素贝叶斯模型处理。
模型训练：
- 用多项式朴素贝叶斯模型训练上述向量化数据及其对应标签。
测试样本准备：
- 准备了6个测试句子，包含明显的正面、负面以及混合情感表达。
- 用同一向量化器转换测试文本。
降维处理：
- 使用PCA将训练和测试的高维词频向量降到二维，方便后续可视化。
可视化：
- 训练数据点在二维空间中绘制，正面样本用红色，负面用蓝色。
- 测试数据点用绿色星号（预测正面）和紫色星号（预测负面）标记，并注释对应文本和预测类别。
输出结果：
- 打印每个测试文本的预测类别。

直观现象：

由于合成数据中正负词汇完全区分，朴素贝叶斯模型能够轻松学习词汇与类别的对应关系。
PCA可视化显示训练样本清晰聚类，正负样本分布明显。
测试样本中，词汇主要来自正面或负面集合的点聚集在对应类别附近。
混合情感的测试样本分布在两类之间，预测结果也体现出一定的不确定性。

这段代码有效地展示了朴素贝叶斯如何利用词汇分布进行文本分类，以及PCA如何帮助我们在二维空间中可视化高维文本数据的结构。

爱酱也发过LDA、PCA等降为方法的仔细文章介绍，有兴趣的伙伴可以去看看哦～
线性判别分析（LDA）文章传送门：
【AI深究】线性判别分析（LDA）全网最详细全流程详解与案例（附大量Python代码演示）|数学原理、案例流程、代码演示及结果解读|LDA与PCA的区别、实际业务中应用、正则化与扩展、多类别决策边界-优快云博客

主成分分析（PCA）文章传送门：
https://blog.youkuaiyun.com/ai_aijiang/article/details/148799217?spm=1011.2415.3001.5331

六、进一步分析与工程启示

为什么这种构造的数据效果特别好？

词汇完全分离：正面和负面样本各自只用“自家”词汇，训练集中没有任何词汇重叠。朴素贝叶斯模型在这种条件下几乎不会混淆类别。
样本数量均衡且足够：每类20个样本，模型能充分学习每个词和类别的对应关系。
测试样本分布清晰：测试文本要么全用正面词，要么全用负面词，或两者混合，模型的预测和可视化都很直观。

七、可视化结果的进一步解读

PCA降维后，红蓝点（训练样本）形成明显的两个聚类，正面和负面样本在二维空间中分区清楚。
绿色星号（测试样本）落在对应类别的聚类附近，说明模型判断与数据结构高度一致。
混合情感的测试样本（如“awesome awesome bad”）位置靠近两类之间，模型预测可能受主导词影响，体现了朴素贝叶斯的“加权投票”机制。
注释文本和预测标签，让观众可以一眼看出模型的判断过程和依据。