大家好,我是爱酱。本篇将系统讲解主成分分析(PCA, Principal Component Analysis)的原理、数学推导、案例流程、代码实现和工程建议。内容适合初学者和进阶读者,分步解释,配合公式和具体例子。
注:本文章含大量数学算式、详细例子说明及大量代码演示,大量干货,建议先收藏再慢慢观看理解。新频道发展不易,你们的每个赞、收藏跟转发都是我继续分享的动力!
开始前,爱酱之前也介绍过另外一种分析方法——线性判别分析(LDA)。有兴趣的伙伴可以在看完PCA之后去去看看喔~
传送门:【AI深究】线性判别分析(LDA)全网最详细全流程详解与案例(附大量Python代码演示)|数学原理、案例流程、代码演示及结果解读|LDA与PCA的区别、实际业务中应用、正则化与扩展、多类别决策边界-优快云博客
学习PCA的过程中会用到特征向量(Eigenvector)与特征值(Eigenvalue)的概念。如果看不懂,爱酱也有仔细介绍这两概念的文章哦~
传送门:
【AI概念】特征向量(Eigenvector)与特征值(Eigenvalue)是什麽?他们有什么区别?各自在机器学习中担任什么样的角色?| 求解方法、具体例子、几何动画与代码直观演示、实际工程应用场合-优快云博客
我们正式开始吧!
一、PCA算法简介
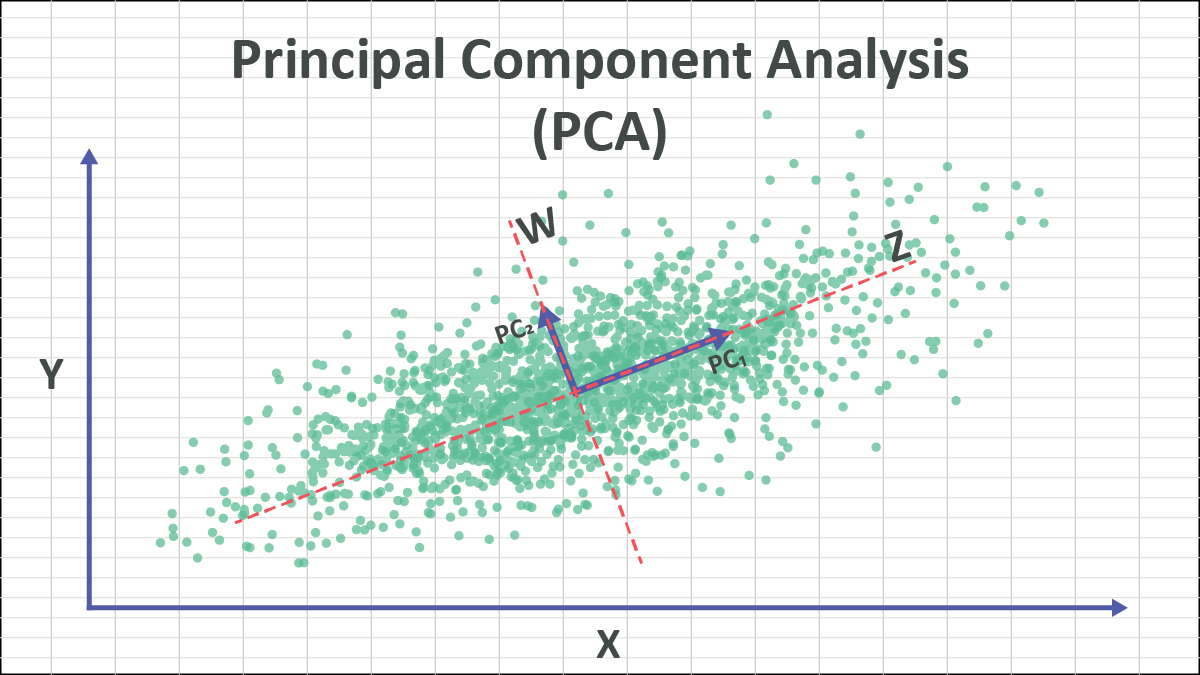
主成分分析(PCA)是一种经典的无监督降维方法,广泛应用于数据压缩、特征提取、可视化等领域。PCA的核心思想是:找到数据方差最大的方向,将高维数据投影到这些主方向上,从而达到降维和去冗余的目的。
二、PCA的数学原理
1. 目标与思想
PCA希望在保留数据主要信息的前提下,把原始高维数据投影到低维空间。其目标是:
-
最大化投影后数据的方差(信息量最大)
-
不同主成分之间相互正交(无关)
2. 协方差矩阵
假设有个样本,每个样本
维,记为
,先对每个特征做中心化(减去均值),然后计算协方差矩阵:
3. 特征值分解
PCA的核心是对协方差矩阵做特征值分解:
其中为特征向量(主成分方向),
为特征值(该方向上的方差大小)。
4. 主成分选择与降维
-
取最大的
个特征值对应的特征向量
,组成投影矩阵
。
-
将原始数据
投影到
上,得到降维后的数据
:
三、PCA案例流程
Step 1:准备数据
-
收集原始高维数据,常见于图像、文本、传感器等领域。
-
对每个特征做中心化(减去均值)。
Step 2:计算协方差矩阵
-
用中心化后的数据计算协方差矩阵
。
Step 3:特征值分解
-
对
做特征值分解,得到特征值和特征向量。
Step 4:选择主成分
-
选取最大的
个特征值对应的特征向量,作为主成分方向。
Step 5:数据投影与降维
-
用主成分方向将原始数据投影到低维空间,得到降维结果。
四、PCA代码演示(二维可视化案例)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
# 1. 加载Iris数据集(4维特征)
data = load_iris()
X = data.data
y = data.target
# 2. 用PCA降到2维
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
# 3. 可视化降维结果
plt.figure(figsize=(8,6))
for label, color in zip(np.unique(y), ['red', 'green', 'blue']):
plt.scatter(X_pca[y==label, 0], X_pca[y==label, 1], label=data.target_names[label], color=color)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('PCA of Iris Dataset')
plt.legend()
plt.show()
# 4. 查看主成分方差贡献率
print("Explained variance ratio:", pca.explained_variance_ratio_)
五、代码流程与结果解读
-
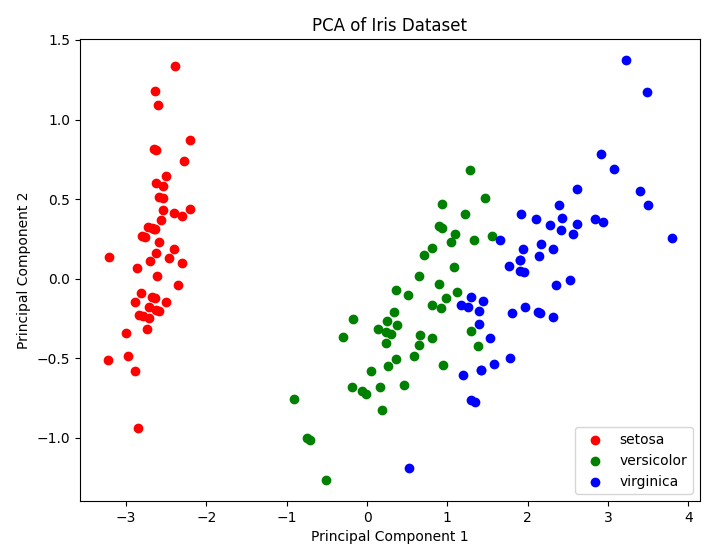
用Iris数据集(4维)演示PCA降维到2维,便于可视化。
-
降维后不同类别的花在主成分空间中分布较开,便于后续分类或聚类。
-
explained_variance_ratio_显示每个主成分方向解释的方差信息量,反映降维后信息保留程度。
六、PCA的几何意义与主成分选择
1. 几何意义
-
PCA实质上是在高维空间中,选择一组新的正交坐标轴(主成分方向),这些轴按照数据方差从大到小排序。
-
第一个主成分方向(PC1)是数据方差最大的方向,第二个主成分方向(PC2)与PC1正交,且方差次大,以此类推。
-
数据在主成分方向上的投影,保留了原始数据中最“有用”的信息(即最大方差)。
2. 主成分选择标准
-
常用累计方差贡献率(cumulative variance contribution rate)来决定保留多少主成分。比如累计贡献率达到95%时,说明降维后数据保留了95%的信息。
-
数学表达:
其中
为第
个特征值,
为主成分数,
为原始特征数。
七、PCA与LDA的对比
| 方法 | 类型 | 是否有监督 | 目标 | 投影方向依据 | 适用场景 |
|---|---|---|---|---|---|
| PCA | 无监督 | 否 | 最大化投影后方差 | 整体数据方差 | 数据压缩、可视化 |
| LDA | 有监督 | 是 | 最大化类间距离/最小化类内距离 | 类别分离 | 分类、降维 |
-
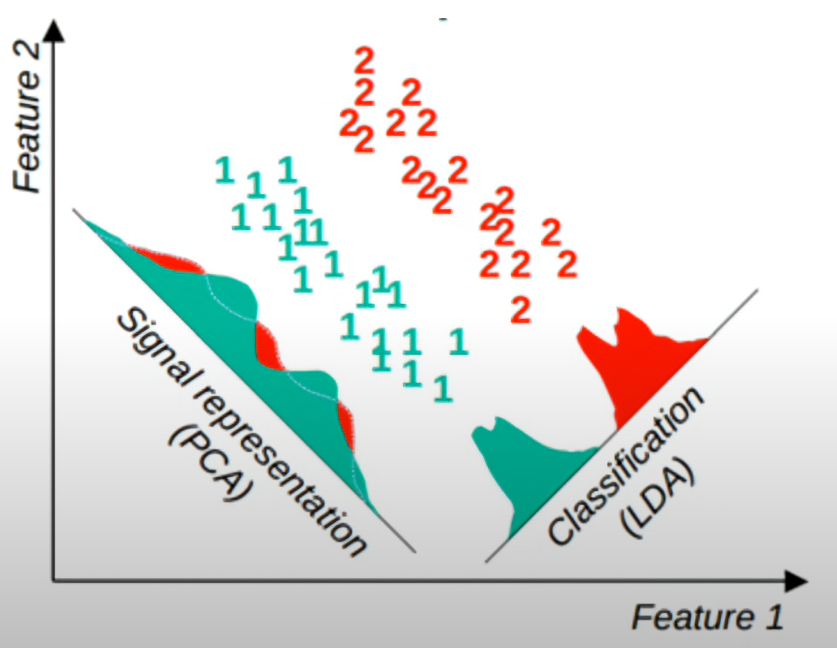
PCA只考虑数据的整体分布,不利用类别信息,适合数据预处理、降噪、可视化。
-
LDA利用类别标签,优化类别分离,适合分类任务的降维。
详细可以阅读爱酱在LDA文章的描述,有对两个方法更仔细的描述。由于部分对比内容重复(在LDA文章已经覆盖了),这里就不详细讲了。LDA文章的传送门在一开始给了大家。
八、PCA的实际应用场景
PCA在各类工程和科学领域有广泛应用:
-
数据压缩:如图像压缩,保留最重要的主成分,大幅减少存储空间。
-
特征提取:在机器学习前用PCA提取主成分,提升模型性能。
-
数据可视化:高维数据降到2维或3维,便于可视化和聚类分析。
-
去噪:去除主成分方差很小的噪声维度,提升信号质量。
-
金融分析:用PCA分析股票收益的主因子,风险管理。
-
基因数据分析:PCA用于基因表达数据降维,发现主要变异方向。
九、PCA工程建议与优缺点
工程建议
-
特征需标准化或归一化,避免尺度影响主成分方向。
-
合理选择主成分数,兼顾信息保留和降维效果。
-
可结合可视化和累计方差贡献率,判断降维效果。
-
对于非线性数据结构,可考虑核PCA等扩展方法。
优点
-
算法简单高效,易于实现。
-
能有效压缩数据,去除冗余和噪声。
-
有助于可视化和理解高维数据结构。
缺点
-
只保留线性关系,无法处理复杂非线性结构。
-
主成分难以直接解释原始特征的实际意义。
-
对异常值敏感。
十、总结
PCA作为最经典的无监督降维方法,通过特征值分解协方差矩阵,提取数据最主要的变异方向,广泛应用于数据压缩、特征提取、可视化等领域。理解PCA的原理和几何意义,对深入掌握数据分析和机器学习算法具有重要意义。实际工程中,建议结合特征预处理、主成分选择和可视化,提升数据建模和分析能力。
如需讲解核PCA、PCA与SVD的关系、PCA在图像处理/推荐系统/信号处理等领域的案例,欢迎继续提问!
谢谢你看到这里,你们的每个赞、收藏跟转发都是我继续分享的动力。
如需进一步案例、代码实现或与其他聚类算法对比,欢迎留言交流!我是爱酱,我们下次再见,谢谢收看!
























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








