详细解释为什么局部坐标系下的变换矩阵需要右乘，全局坐标系下的变换矩阵需要左乘，绝对能看懂！（计算机图形学）

详细解释为什么局部坐标系下的变换矩阵需要右乘，全局坐标系下的变换矩阵需要左乘（计算机图形学）

矩阵变换的过程，实际上就是一个从局部坐标逐步地转化为相对坐标的一个过程。
假设一开始的坐标是(x,y,z)，这是平移、缩放、旋转等任何操作发生之前，模型在绝对坐标系中的位置。

但我们也可以将(x,y,z)理解为在局部坐标系中的坐标。我们要做的就是通过一系列的变换矩阵，将其转化为模型在绝对坐标系中的位置

但是这里存在一个问题，变换可以是局部变换也可以是绝对变换。

局部变换，是在局部坐标系上考虑问题，所有的坐标都是相对坐标，还没有被转化为绝对坐标
绝对变换，是在绝对坐标系上考虑问题，所有的坐标都是绝对坐标。

我们以任意一种矩阵变换为例。
例如平移矩阵：

代表向着x移动2，向着y移动1
1.如果是绝对坐标系中的平移，很自然，我们把它放在累积变换矩阵T的左边就行了。
为什么可以这样做呢?
假设初始时模型在绝对坐标系中的位置为(x,y,z)，累积变化矩阵为M（记一下这个词，后面将反复提到），那么:

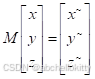
其中

代表了经过一些变化后模型目前所处的位置。如果还想继续移动，再用这个平移矩阵左乘当前坐标就行了，这不难理解

2.如果是局部坐标系中的平移，我们现在将变换矩阵作为考虑的主体。
假设经过一系列变换以后，目前累积到的变换矩阵为

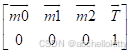
在这里， 实际上是目前局部坐标系中的三个基向量。
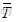代表在绝对坐标系中三个方向上的位移。我们在目前这个局部坐标系中的位置为
。

不难发现，在当前这个局部坐标系中，其上任意位置的坐标都能通过TF映射为在全局坐标系中的相应位置。那很自然地，在局部坐标系中，(x+2,y+1)这一点是(x,y)在x方向移动2，y方向移动1。显然这个点也能通过TF正确地被映射为全局坐标系中的对应位置。并且它是我们施加了平移变换后，在目前这个局部坐标系上的位置。当然一旦平移，当前这个局部坐标系就不再是有效的局部坐标系了（当然这个我们不用关心）。

因此，我们可以先对点(2,1)施加平移变换，然后再通过M映射为绝对坐标系上的点。
也就是说，局部坐标系中的平移操作，需要通过累积变化矩阵来右乘该平移矩阵。

上述的平移操作可以推广至缩放操作和旋转操作，是相同的道理。
综上所述，最终的规律为：
a.如果是局部坐标系下的操作，则让累积变换矩阵在左，此步的变换矩阵在右
b.如果是全局坐标系下的操作，则让累积变换矩阵在右，此步的变换矩阵在左。