为什么在透视投影变换中，z的映射关系不是线性的？

首先我们要理解：
透视投影变换，它实际上所做的事情是将摄像机点，近平面，远平面这三者组成的台体区域中的任意一点，映射成为一个长方体区域中的任意一点。如下图所示

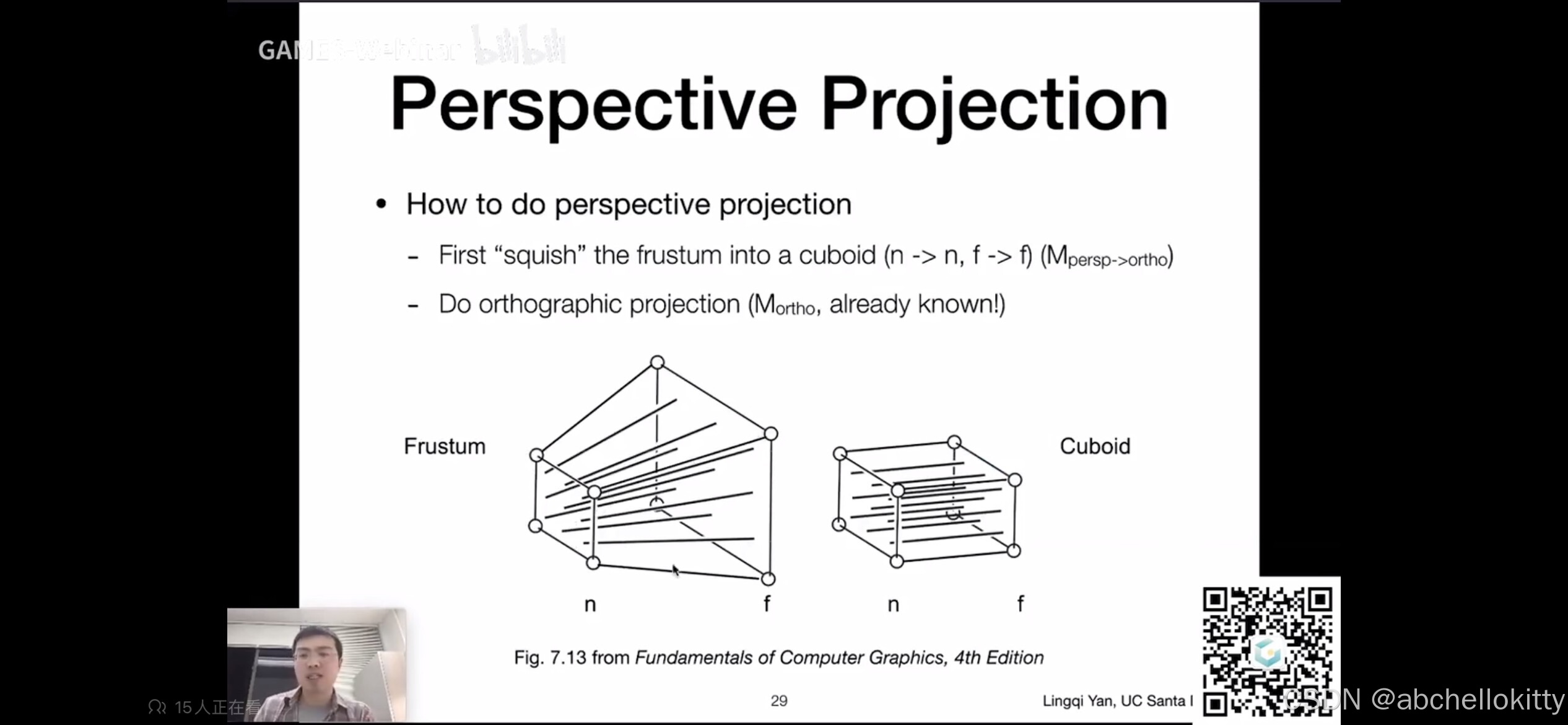
映射成为长方体以后，我们就可以仿照平行投影的做法，进一步将其转化为ndc坐标。

假设映射前和映射后的点分别为
（xe,ye,ze),(xp,yp,zp)
在这里，xp和yp直接反映了原来的那个点在投影面上的位置。所以必须严格遵守相似三角形的比例关系，即xp=-n·xe/ze，yp=-n·ye/ze。
而zp的主要目的是为了表示投影面上同一位置的两个像素点的深度关系。因此它只需要满足ze和zp是正相关的即可。并且边界情况需要对应上，即当ze=-n时，zp=-n；ze=-f时，zp=-f。
一种最容易想到的做法是让zp=ze，这样做达到了正相关的目的，并且满足边界情况。但是不能落地实现。具体的原因后面会讲。

但是直接求（xe，ye，ze，1)到(-n·xe/ze，-n·ye/ze，zp，1）的关系是困难的，因为矩阵只能表示线性关系，不能做除法，需要消掉ze对x和y结果的影响。

我们需要明白，在三维空间上，点的齐次坐标（x，y，z，1）与（x·w，y·w，z·w，w）是等价的。
为了消除x和y对于ze的依赖，可以让w=-ze。
于是我们引入了剪裁坐标（n•xe，n•ye，-zp·ze，-ze）。
我们设这样的剪裁坐标为(xc，yc，zc，wc）

那么我们现在要求取的关系就变成了到(xe，ye，ze，1）到 (xc，yc，zc，wc）的关系。

这里就可以解释为什么zp不等于ze，因为如果zp等于ze，那么zc=-ze^2，这样的关系是不能通过矩阵表示的。

但是如果zc和ze的是线性相关的，并且当ze=-n时，zp=-n；ze=-f时，zp=-f。这样的矩阵是实际存在并且能被求出来的，并且此时zp和ze仍然是正相关的，且符合边界条件。这样的变换矩阵就达到了 我们一开始所说的目的：
1.xp和yp严格遵守相似三角形比例。以确保透视投影的正确性。
2.zp和ze正相关，并且符合边界条件。以确保像素之间的深度关系。

我们已经知道：zp和ze并不是呈线性关系，接下来，我们尝试认识一下zp和ze应该是什么样的变化关系。
首先我们求取原坐标到剪裁坐标的变换矩阵M：
显然M是一个4乘4的矩阵，并且满足

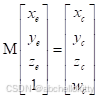
由于xc=nxe,yc=nye,wc=-ze
所以我们可以先求出第1行的元素为(n,0,0,0)，第2行的元素为(0,n,0,0)，第4行的元素为(0,0,-1,0)
而第3行的前两个元素应该为0，因为zc和xe、ye无关。
于是我们初步得到下面的矩阵

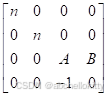
于是A·ze+B=-zp·ze
又因为当ze=-n时，zp=-n，zc=-zp·ze=-n^2
当ze=-f时，zp=-f，zc=-zp·ze=-n^2
代入得

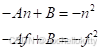
解得A=n+f，B=n·f
所以变换矩阵为

所以zc=-ze·zp=(n+f)·ze+n·f
可以得出zp和ze的关系为

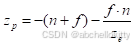
于是

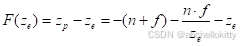
我们尝试探究F(ze)关于ze的单调性，可以对ze进行求导

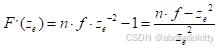
我们按不同区间对其进行分析：

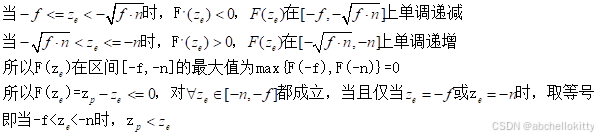
综上所示，我们得出最终结论：
在远平面和近平面中间的任意一点，其所投影的z值相比原来的z值更加趋近于远平面，远离近平面。