【电机控制】开环全正弦无感FOC

　　从７月初开始调试全正弦的无感FOC，因为前期的准备工作已经做了许多，前面使用有霍尔的BLDC电机，测试了状态观测器的角度估计波形，速度检测等等，模拟无感BLDC的条件，虽然经历了波折，在有霍尔BLDC电机上还算是比较顺利，关于状态观测器的调试也有了一些经验。

       调试有霍尔电机时，测试了方波切换正弦波，使用霍尔传感器来反馈电角度，然后程序中加入观测器，来对比估计电角度与实际电角度，具体的实验结果请看上一篇博客，不过那时的博客是快两个月前的，后面调试的波形会比那个好很多。

       在对比估计电角度差不多之后，在程序流程中便加入一个新流程，状态观测器正弦波流程，使用状态观测器的估计角度来替代霍尔传感器的测量电角度，也一切顺利，后面便开始调试抛弃方波，全正弦波的无感FOC。

                                                                        

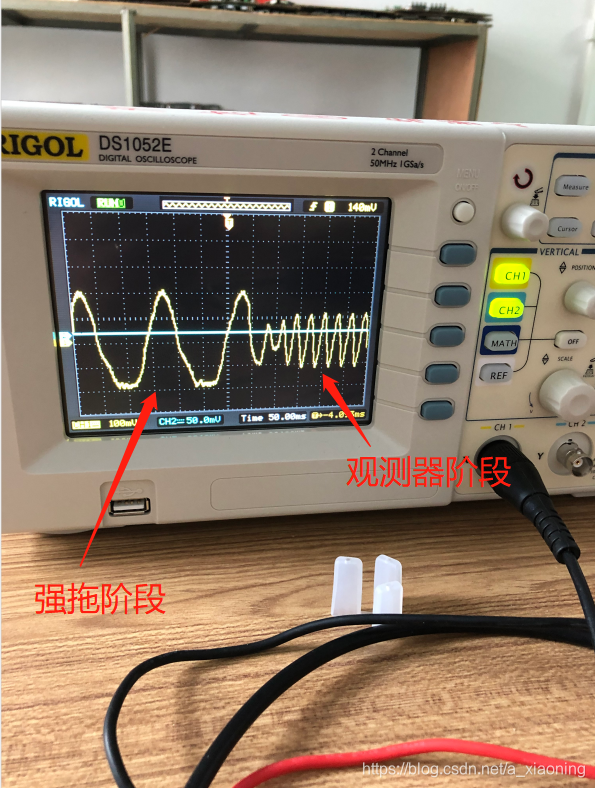
        流程也是类似，强拖+观测器，最开始使用的是功率小的电机，参数也不是很好调，大概搞了一周，可以转了，整理了一波调试心得笔记。于是乎，准备动真格的，调试目标电机，目标电机功率就比测试电机大了，当然，也是低压电机，24V，空载正常转就有1A左右了，换了电机也就换了一波电机参数。怀着对未来的期盼与担忧，我开干了。

        果然，刚开始基本完全不能运行，包括强拖阶段也是一样。额，这就极度尴尬，虽然我已经做好了迎接困难的准备，没想到这么难，自信心被轻微打击。

                                                                  

       整理思路，从启动状态开始更改，然后更改观测器，启动状态还是比较好改的，毕竟就是个强拖，观测器就难受了，活活被卡了三个星期，最后还是跟微芯工程师交流了一下，给了他们一个电机，老工程师果然是老工程师啊，他一天就搞完了，在他的启发之下，卡了三个星期的观测器，终于让电机转起来了。果然我这新人，在老工程师面前还是相当稚嫩啊。

       在没有调出来的三个星期内，甚至怀疑过强拖+观测器这种控制模式是不是可行，如果方案有问题，那怎么调都白瞎啊。在后面的几天，我还去看了一下高频注入，了解了一下ST是怎么做的。简单来说，只要是强拖，就免不了有反转的问题，这是这种启动方案的固有弊端，高频注入可以在零速状态下就检测到初始电角度，然后ST是在零速以及低速状态下使用高频注入，在中速时，高频注入与观测器配合使用，在高速时使用观测器。这样乍一看，是看不出什么猫腻，但是仔细一想，为什么ST在低速时要使用高频注入呢？初始电角度已经检测出来，那么直接使用观测器不好吗？当然，ST这样做肯定有这样做的道理，唯一的解释就是观测器并不适合低速使用。

        带着这个猜测去验证了一下，似乎真的是这样的原因，后来看到微芯工程师说了有一个最低转速的参数，因为他们也是用强拖+观测器这种方案。证明猜想正确，不过我暂时还没空去深入学习高频注入了，因为稍微看了一下，高频注入的C代码，一看就不好写，单带通，低通，高通滤波器就得写一阵子，还不说单独设计滤波器，就是直接采用现有的几个滤波器，C程序也并不好写，此外还要考虑单片机运算能力，我用的32F103，当然，ST的库都已经出来了，说明32的运算能力还是可以运行，只是我要再重新撸代码的话，一开始肯定会有计算时间的问题，然后优化代码，这些等后面调完力矩什么的，再考虑吧。真的是，电机控制的东西，越搞越多，越搞越深。

       总结来说，按照老工程师的启发，观测器本身一般是没什么问题的，因为我之前怀疑过是不是观测器本身模型建的不对什么的，主要还是针对这种电机的阻感参数，以及最低转速要注意。刚开始不知道有最低转速，稍微吃了点亏。

       目前，整个程序还是一个开环系统，因为我现在使用的电路板并不适合现在用的电机，所以闭环要等一段时间再调了，现在准备先把撸代码的工作放一放，先针对现在的电机设计一款测试板，现在的板子也有很多地方想要加功能什么的。

        加油吧，回首看一下自己写的FOC代码，FOC文件夹都已经180kb了，而且很多保护性的程序还没开始写，已经稍微有点大了。为了转这个电机，撸了这么多代码，要我现在看，我自己都感觉有点不可思议，虽然还有很多bug有待解决，一步一步来吧，现在的目标已经越来越清晰了。