本文探讨了现代控制理论在机器人轨迹控制中的应用，利用Matlab和OctaveOnline解决复杂控制问题。通过调整机器人左右轮速度，实现了直线、圆周及曲线等多种运动轨迹。文章深入分析了正弦曲线轨迹的实现方法，以及高等数学理论在路径规划中的作用。
大部分现代控制理论习题都可以通过计算机辅助解决，如Matlab或Octave Online。
这里，重点推荐Octave Online，如下图所示，无需安装，直接打开网页使用：
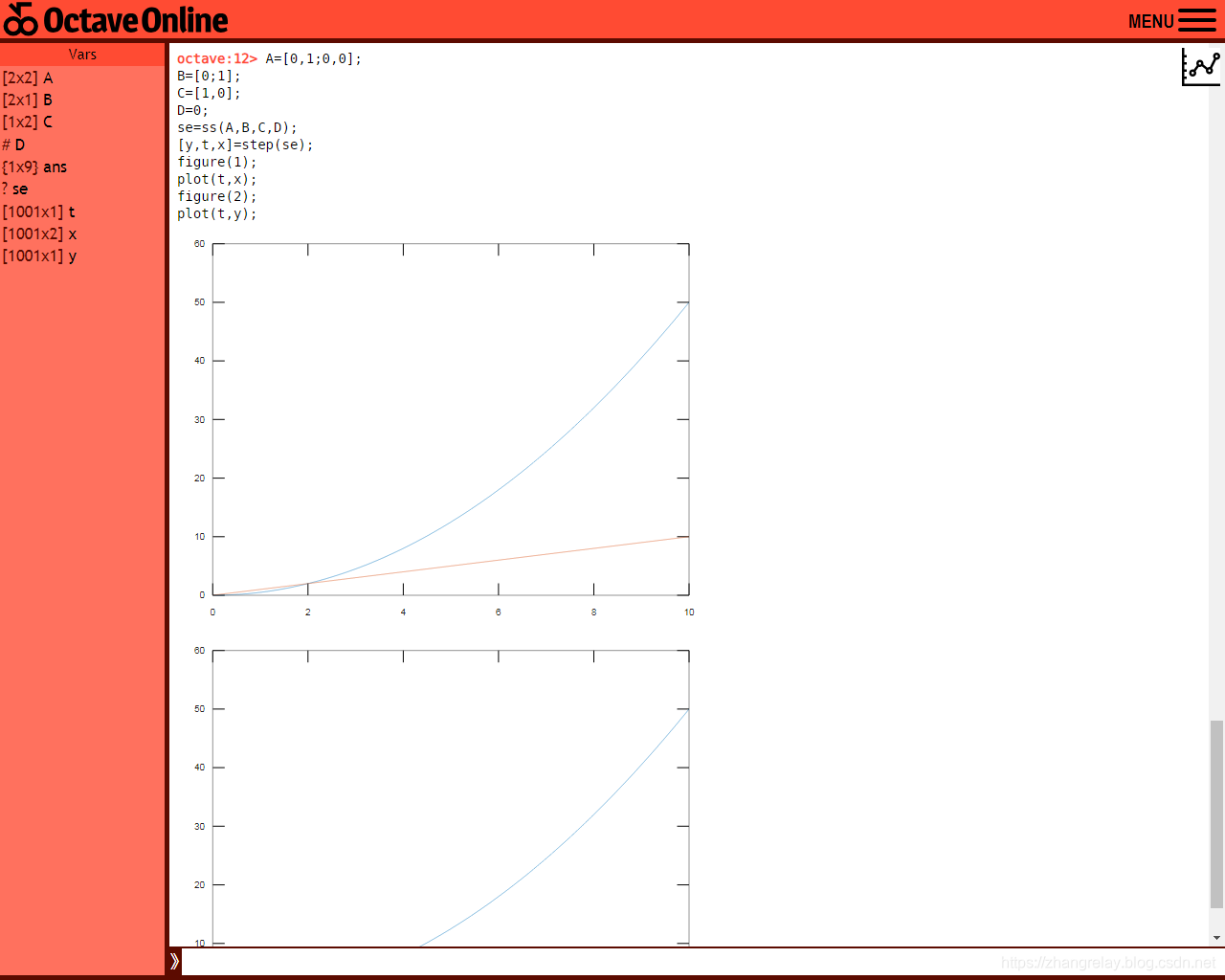
在上一篇中讲述了最常见的地面差动机器人的状态方程，那么其解是什么形式呢？
https://blog.youkuaiyun.com/ZhangRelay/article/details/88033016
给定初始位置和左右轮的速度，机器人就可以绘制出在二维平面空间运动轨迹。
依据左右轮速度得到轨迹为正解，依据轨迹求左右轮速度为逆解。
观察下面图示，并编写程序控制机器人左右轮速度实现如下二维空间运动轨迹，直线，圆，曲线等。
思考题：机器人轨迹为正弦曲线，如何实现？（此部分为移动机器人运动控制路径规划方向的基础）
烧脑题（无需完全一致的路径图案，相似即可）：
需给出数学推导公式和对应实现的代码，思考高等数学中，连续，一致连续与上述路径曲线的关系？
扩展阅读：系统稳定性之barbalat引理
扫一扫
3208
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
