Matlab simulink建模与仿真第三章（连续模块库）

Zevalin爱灰灰

已于 2024-09-05 00:54:25 修改

阅读量4.6k

点赞数 14

分类专栏： MATLAB使用速成文章标签： matlab 开发语言

于 2024-08-24 23:54:48 首次发布

本文链接：https://blog.youkuaiyun.com/Zevalin/article/details/141507510

版权

MATLAB使用速成专栏收录该内容

31 篇文章

订阅专栏

参考视频：simulink1.1simulink简介_哔哩哔哩_bilibili

一、连续模块库中的模块概览

1、连续时间线性系统模块

注：积分模块在第二章中有介绍，本章不再赘述；二阶积分模块相当于两个积分模块串联（可以设置两个初始条件），本章也不会对二阶积分模块进行详细介绍；带上下限的积分模块和带上下限的二阶积分模块默认激活“Limit output”选项，本章也不会对它们进行详细介绍。

2、连续时间延迟模块

二、连续微分模块

1、Derivative连续微分模块的使用

（1）当输入信号为连续信号时，可以使用Derivative连续微分模块对信号求微分，而当输入信号为非连续信号时，只能使用Difference离散微分模块对信号求微分，否则结果可能是不准确的。

（2）连续微分模块是用数值算法求微分，所以其微分结果仅仅是理想结果的一个近似，具体精度取决于仿真的步长，步长越小，仿真的结果越精确。

（3）连续微分模块在初始时刻t=0的输出为0。

2、Derivative连续微分模块的缺陷与解决办法

连续微分模块会将系统中的噪声放大，在实际搭建系统时是不推荐使用该模块的。其实微分模块就相当于一个s算子，其传递关系的拉氏变换如下所示，可以将这个s算子和受控信号合并，也就是和其它模块合并，这样就不用使用连续微分模块了，当然，解决办法并不止这一种，只要通过数学推导能将微分环节去除，都可以避免使用该模块。

三、状态空间模块

1、状态空间方法

（1）当一个系统有多个输入或者多个输出时，用传统的传递函数进行分析是很困难的，这时可以使用状态空间法建立系统的数学模型，如下所示，其中u是输入信号，x是状态变量，y是输出信号，当输入/输出信号为向量时，表示有多个输入/输出，相应的微分方程也应该不止一条。

（2）要想建立状态空间模型，首先需要选择合适的状态变量，其次需要求解矩阵A、B、C、D，下面以一个四阶常系数线性微分方程为例，演示如何求解A、B、C、D四个状态矩阵。

①首先寻找状态向量和状态矩阵，一般情况下选择的状态变量都等于需要求解的原函数本身或者其导数（总之选取方式不唯一，求出的状态矩阵也不唯一）。

②根据选取的状态变量，可以得到如下关系，需要说明的是， $\dot{x}$ 表示 $x$ 的一阶导数。

③根据上面列出的关系，可以写出第一个方程，从而求出矩阵A、B。

④根据 $x_{1}=y\left (t \right )$ ，可以写出第二个方程，从而求出矩阵C、D。

2、State Space状态空间模块

使用状态空间法求出四个矩阵后，可以直接将输入信号接进状态空间模块，该模块将会输出求解结果。

3、利用linmod函数提取状态矩阵

（1）注意事项：

①linmod函数适用于连续系统，对离散系统需要使用dlinmod函数。

②使用linmod函数时系统中不应包含连续微分模块，若存在微分环节，可以使用Switched derivative模块代替连续微分模块。

（2）linmod的可选参数较多，一般常用的形式有以下两种：

①linmod(‘sys’)：’sys’是要从中提取线性模型的Simulink系统名称；MATLAB自行识别状态向量和输入信号向量。

②linmod(‘sys’,x,u)：’sys’是要从中提取线性模型的Simulink系统名称；x用于指出状态向量，u用于指出输入信号向量。

（3）沿用上例的四阶常系数线性微分方程，演示使用linmod函数提取状态矩阵：

①首先根据微分方程将系统搭建，这里可以使用微分模块搭建，也可以使用传递函数模块搭建，这里以传递函数模块为例，传递函数是不关心输入和输出的，只关心它们之间的关系，所以其输入端口和输出端口用输入输出模块堵死即可，然后保存该模型文件至当前工作目录。

②在命令窗口输入“a = linmod(‘eg3_3’)”（“eg3_3”是刚刚保存文件的文件名），linmod会以结构体的形式返回四个矩阵给变量a。

四、传递函数模块

1、传递函数简介

（1）传递函数是指零初始条件下线性系统响应（即输出）量的拉普拉斯变换（或z变换）与激励（即输入）量的拉普拉斯变换（或z变换）之比，连续传递函数记作G(s)=Y(s)/U(s)，其中Y(s)、U(s)分别是输出量和输入量的拉普拉斯变换。

（2）以一个二阶低通滤波器电路为例，如下图所示。

①电容写成复数阻抗的形式，借助电路相关理论进行计算，可以得出传递函数G(s)。

②为简单起见，设电阻大小均为1Ω，电容大小均为1F，则有

2、Transfer Fcn传递函数模块

（1）传递函数模块只有一个输入端口和一个输出端口，双击模块可以设置传递函数分子和分母的多项式系数（非最高次项若系数为0，切记不要省略）。

（2）上例二阶低通滤波器的仿真结果如下图所示。

五、零极点增益模块

1、Zero-Pole零极点增益模块

（1）零极点增益也是用来描述传递函数的，它可以和传递函数互相转换，用零极点增益表示时能很方便地看出其对应传递函数的零点、极点和增益。

（2）双击零极点增益模块，可以直接编辑对应传递函数的零点、极点和增益。

2、tf、zpk、ss函数

（1）tf、zpk、ss这三个函数可以实现传递函数在一般形式、零极点增益形式和状态空间形式（含四个矩阵的结构体表示）之间互相切换。

（2）tf函数构造一般形式传递函数：只要在第一个参数输入传递函数分子多项式系数矩阵，在第二个参数输入传递函数分母多项式系数矩阵，即可构造出一般形式传递函数。

（3）zpk函数构造零极点增益形式传递函数：该函数的第一个参数是零点集，第二个参数是极点集，第三个参数是增益，zpk函数根据这三个参数构造出零极点增益形式传递函数。

（4）ss函数构状态空间形式传递函数：将A、B、C、D四个矩阵依次作为ss函数的参数，ss函数会根据四个参数构造出状态空间形式传递函数，以含四个矩阵的结构体形式返回。

（5）tf函数、zpk函数和ss函数，它们的参数还可以是一般形式、状态空间形式（含四个矩阵的结构体表示）或者零极点增益形式的传递函数，执行的功能是将传递函数转化为另一种表现形式，比如将含四个矩阵的结构体作为tf函数的参数，tf函数会根据这个结构体构造出一般形式的传递函数。（下图中的传递函数f与上图相同）

六、PID控制模块

1、PID Controller模块

（1）PID控制模块实现了连续和离散时间 PID 控制算法，并具有防倒转、外部复位和信号跟踪等高级功能。

（2）双击PID控制模块，可打开其配置窗口。

①如下所示，可以配置比例参数（Proportional）、积分参数（Integral）和微分参数（Derivative），并且可以设置初始条件（Initial conditions）、外部重置功能（External reset），后两个设置在积分模块中曾介绍过，和PID控制模块大同小异，这里不再赘述。

②点击“Tune...”按钮，可以打开PID调节器以调节PID参数。

③在高级选项中，可以激活“Limit output”选项，以设置饱和上下限以及抗饱和方法（Anti-windup method），另外还可使能追踪模式（勾选“Enable tracking mode”），并配置追踪系数。

④PID控制器的类型可以是理想的（Ideal），也可以是并行的（Parallel）。

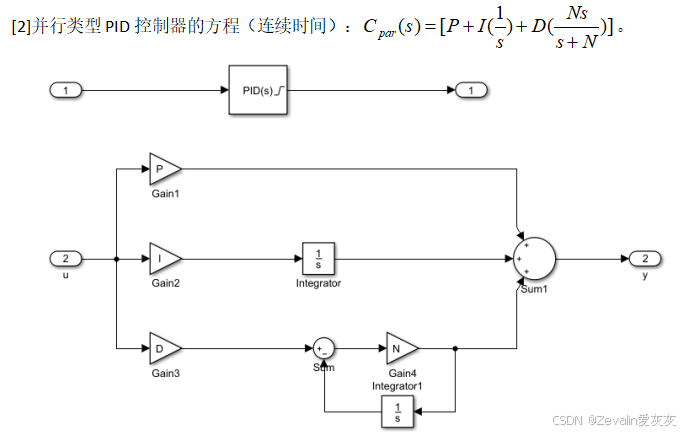
⑤PID控制器有PID、PI、PD、P、I五种形式可选，下面以PI形式为例搭建其等效模型。

2、PID Controller(2DOF)二自由度PID控制器模块

（1）二自由度PID控制器模块与PID控制器模块不同的是，二自由度PID控制器模块增加了一个参考输入端口，可以双击二自由度PID控制器模块，设置参考点（Setpoint）。

（2）二自由度PID控制器模块允许使用参考点作为加权，以实现平稳的设定点跟踪和良好的干扰抑制。

七、几种延迟模块

1、Transport Delay传输延迟模块

（1）传输延迟模块的传输延迟固定，延迟时间可通过双击模块进行设置（延迟时间建议大于仿真步长，否则仿真结果可能不精确）。

（2）因为时延的存在，MATLAB每仿真一步，都要将数据先记录在事先划分好的缓存区中，当延迟时间过长时，事先划分好的缓冲区将会被数据填满，这时MATLAB会自动为该延迟模块划分更多的缓冲区，不过这无疑降低了仿真效率，为了解决这个问题，可以在仿真前就给延迟模块事先划分更大的缓冲区，具体办法为增加延迟模块初始缓冲区的大小。