图的深度优先遍历和广度优先遍历-优快云博客

1、深度优先遍历：简称DFS,从图的某个结点V出发，访问此顶点，然后从V未被访问的邻接点出发深度优先遍历图，直到图中所有与V有路径相通的顶点都被访问到
（1）邻接矩阵的深度优先遍历：

#include<iostream>
#include<vector>
using namespace std; 
struct MGraph{
	vector<char>vex;
	vector<vector<int> >arc;
    vector<bool>visited;
	MGraph(int n){
		vex.resize(n);
		arc.resize(n);
		visited.resize(n);
		int i;
		for(i=0;i<n;i++){
			arc[i].resize(n);
		}
	}
};
void mDFS(MGraph&m,int i){
	int n=m.vex.size();

	cout<<i<<"-"; 
	m.visited[i]=true;
	int j; 
	for(j=0;j<n;j++){
		if(m.arc[i][j]==1&&!m.visited[j]){
			mDFS(m,j);
		}
	}
} 
void mDFSTravel(MGraph&m){
	int n=m.vex.size();
	int i;
	for(i=0;i<n;i++){
		m.visited[i]=false;	
	}
	for(i=0;i<n;i++){
		if(!m.visited[i]){
			mDFS(m,i);	//对未被访问的顶点调用DFS 
		}		    		    
	}//如果是连通图，此循环只会执行一次 
	cout<<"^"<<endl; 
}

int main()
{
	int t;
	cin>>t;
	while(t--){
		int n,i,j;
		cin>>n;
		MGraph mg(n);
		for(i=0;i<n;i++){
			for(j=0;j<n;j++){
				cin>>mg.arc[i][j];//输入边矩阵的信息 
			}
		}
		mDFSTravel(mg);//对图进行深度优先遍历 
	}
	
	return 0;
}

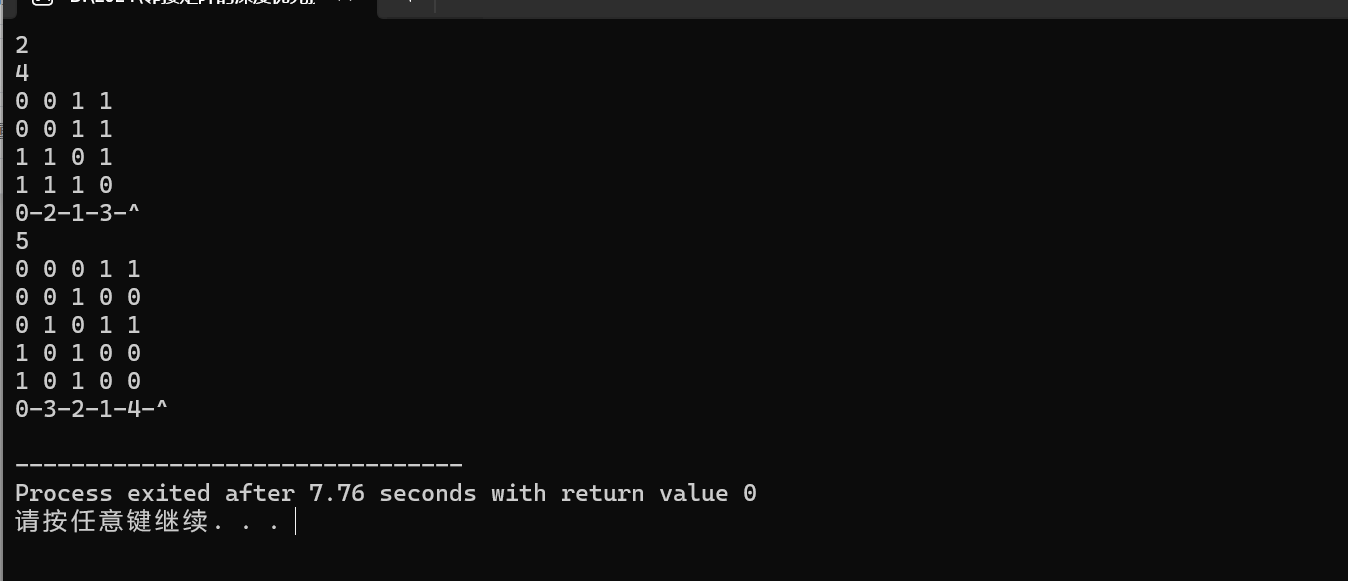
输入输出如下：

(2)邻接表的深度优先遍历：

#include<iostream>
#include<list>
#include<vector>
using namespace std;

struct vertex{
	char vexc;//表示顶点字符 
	list<int>vexl;//表示与顶点相连通的点在顶点数组中的坐标 
};
struct LGraph{//LGraph表示邻接表构成的图(list) 
	vector<vertex>vex;
	vector<bool>visited;
	LGraph(int n){
		vex.resize(n);	
		visited.resize(n);
	}
}; 
int findPos(LGraph lg,char vn){
	int n=lg.vex.size();
	int i;
	for(i=0;i<n;i++){
		if(lg.vex[i].vexc==vn)
		    return i;
	}
	return -1;
}
void creatAdjGraph(LGraph& lg,int n,int k){
	int i;
	for(i=0;i<n;i++){
		cin>>lg.vex[i].vexc;
	}
	for(i=0;i<k;i++){
		char v1,v2;
		cin>>v1>>v2;
		int M=findPos(lg,v1);
		int N=findPos(lg,v2);
		if(M>=0&&N>=0)
		    lg.vex[M].vexl.push_back(N);
	}
}
void lDFS(LGraph&l,int i){
	cout<<i<<"-";
	l.visited[i]=true;
	list<int>::iterator it=l.vex[i].vexl.begin();
	while(it!=l.vex[i].vexl.end()){
		if(!l.visited[*it]){
			lDFS(l,*it);
			break;
		}
		it++;
	}
}
void lDFSTravel(LGraph&l){
	int n=l.vex.size();
	int i;
	
	for(i=0;i<n;i++){
		l.visited[i]=false;	
    }
	for(i=0;i<n;i++){
		if(!l.visited[i]){
			lDFS(l,i);	//对未被访问的顶点调用DFS 
		}		    		    
	}//如果是连通图，此循环只会执行一次 
	cout<<"^"<<endl; 
	
}

int main(){
	int t;
	cin>>t;
	while(t--){
		int n,k;//n表示顶点数,k表示弧数 
		cin>>n>>k;
		LGraph lg(n);
		creatAdjGraph(lg,n,k);
		lDFSTravel(lg);
	}
	return 0;
}

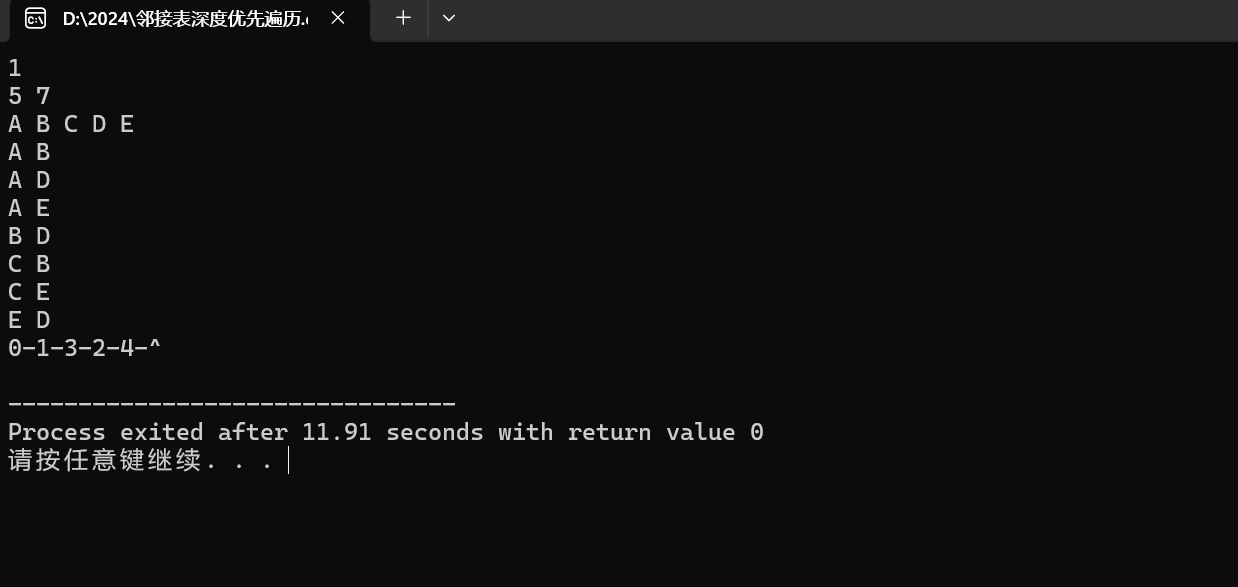
输入输出如下：

2、广度优先遍历：简称BFS,类似于树的层次遍历，即一步步扩大搜索范围，这里可以通过建立一个堆来实现，弹出一个顶点的同时压入其所有相邻而未被访问的顶点

（1）邻接矩阵的广度优先遍历：

#include<iostream>
#include<vector>
#include<queue>
using namespace std; 
struct MGraph{
	vector<char>vex;
	vector<vector<int> >arc;
    vector<bool>visited;
	MGraph(int n){
		vex.resize(n);
		arc.resize(n);
		visited.resize(n);
		int i;
		for(i=0;i<n;i++){
			arc[i].resize(n);
		}
	}
};
void mBFS(MGraph&m, int start) {
    queue<int> q;
    q.push(start);
    m.visited[start] = true;
    
    while (!q.empty()) {
        int i = q.front();
        q.pop();
        cout << i << "-";
        
        int n = m.vex.size();
        for (int j = 0; j < n; j++) {
            if (m.arc[i][j] == 1 && !m.visited[j]) {
                q.push(j);
                m.visited[j] = true;
            }
        }
    }
}

void mBFSTravel(MGraph&m) {
    int n = m.vex.size();
    for (int i = 0; i < n; i++) {
        m.visited[i] = false;    
    } 
    
    for (int i = 0; i < n; i++) {
        if (!m.visited[i]) {
            mBFS(m, i);  
        }               
    }
    
    cout << "^" << endl; 
}
int main()
{
	int t;
	cin>>t;
	while(t--){
		int n,i,j;
		cin>>n;
		MGraph mg(n);
		for(i=0;i<n;i++){
			for(j=0;j<n;j++){
				cin>>mg.arc[i][j];//输入边矩阵的信息 
			}
		}
		mBFSTravel(mg);//对图进行广度优先遍历 
	}
	
	return 0;
}

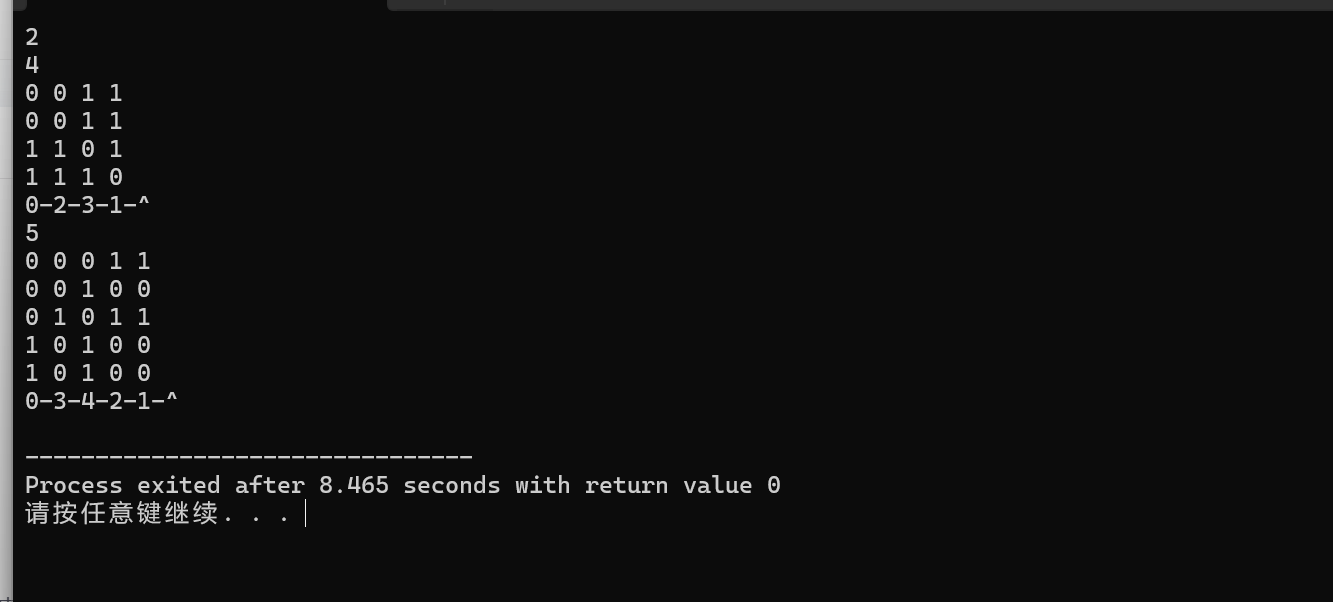
输入输出如下：

（2）邻接表的广度优先遍历：

#include<iostream>
#include<list>
#include<vector>
#include<queue> 
using namespace std;

struct vertex{
	char vexc;//表示顶点字符 
	list<int>vexl;//表示与顶点相连通的点在顶点数组中的坐标 
};
struct LGraph{//LGraph表示邻接表构成的图(list) 
	vector<vertex>vex;
	vector<bool>visited;
	LGraph(int n){
		vex.resize(n);	
		visited.resize(n);
	}
}; 
int findPos(LGraph lg,char vn){
	int n=lg.vex.size();
	int i;
	for(i=0;i<n;i++){
		if(lg.vex[i].vexc==vn)
		    return i;
	}
	return -1;
}
void creatAdjGraph(LGraph& lg,int n,int k){
	int i;
	for(i=0;i<n;i++){
		cin>>lg.vex[i].vexc;
	}
	for(i=0;i<k;i++){
		char v1,v2;
		cin>>v1>>v2;
		int M=findPos(lg,v1);
		int N=findPos(lg,v2);
		if(M>=0&&N>=0)
		    lg.vex[M].vexl.push_back(N);
	}
}
void lBFS(LGraph&l,int start){
	queue<int> q;
    q.push(start);
    l.visited[start] = true;
    
    while (!q.empty()) {
        int i = q.front();
        q.pop();
        cout << i << "-";
        list<int>::iterator it=l.vex[i].vexl.begin();
        while(it!=l.vex[i].vexl.end()){
		if(!l.visited[*it]){
			q.push(*it);
			l.visited[*it]=true;
		}
		it++;
	    }   
    }
}


void lBFSTravel(LGraph&l){
	int n=l.vex.size();
	int i;
	
	for(i=0;i<n;i++){
		l.visited[i]=false;	
    }
	for(i=0;i<n;i++){
		if(!l.visited[i]){
			lBFS(l,i);	//对未被访问的顶点调用DFS 
		}		    		    
	}//如果是连通图，此循环只会执行一次 
	cout<<"^"<<endl; 
}
int main(){
	int t;
	cin>>t;
	while(t--){
		int n,k;//n表示顶点数,k表示弧数 
		cin>>n>>k;
		LGraph lg(n);
		creatAdjGraph(lg,n,k);
		lBFSTravel(lg);
	}
	return 0;
}

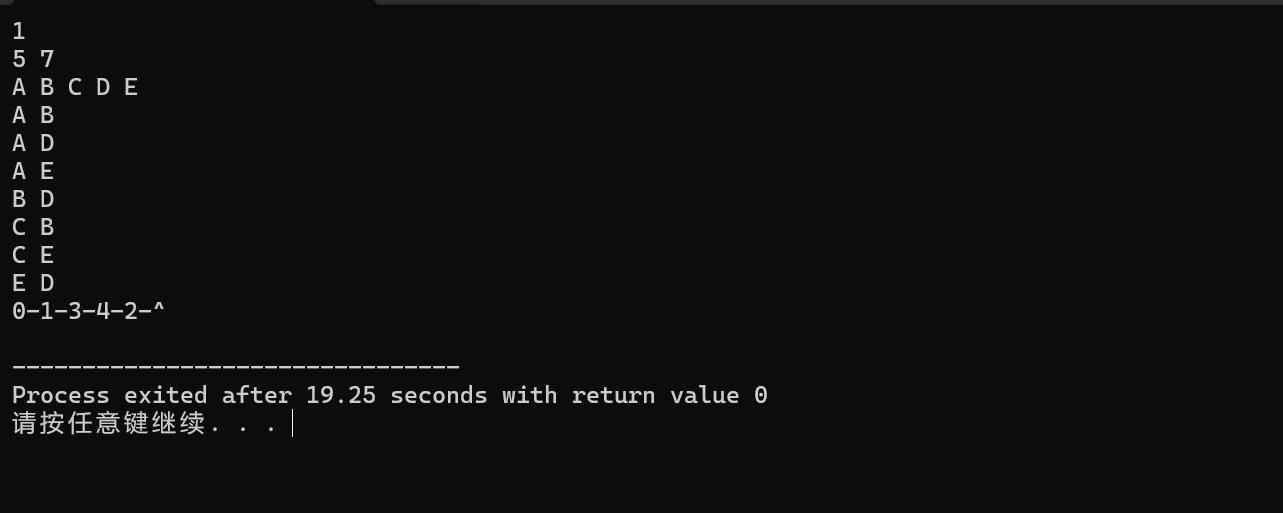
输入输出如下：