一、概念:平衡二叉树是一种高度平衡的二叉排序树,其中每一个结点的左子树和右子树的高度差的绝对值至多为1.
平衡因子(BF):BF=左子树高度-右子树高度
最小不平衡子树:距离插入结点最近,且平衡因子的绝对值大于1的结点的根的子树称为最小不平衡子树
二:平衡二叉树的实现原理:
下面是失衡的四种情况(图片摘自王卓的课程)
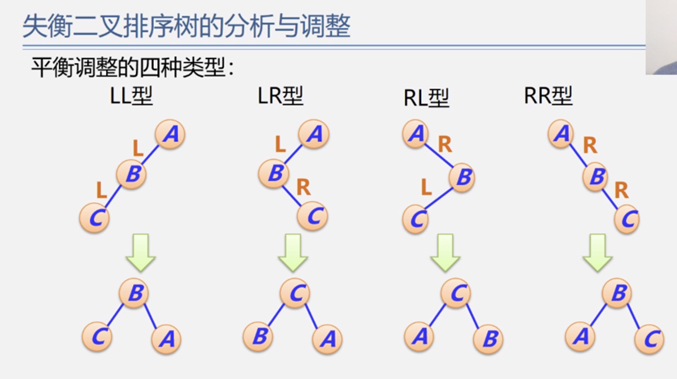
失衡的调整:
1)LL型:
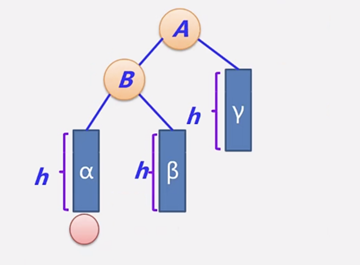
对于LL型失衡需要通过对根结点A进行右旋调整:
- 将 左子节点(B) 提升为新的根节点。
- 原根节点(A)成为 B 的右子节点。
- Y 的原右子树(β)转移到 A 的左子树(保持二叉搜索树的顺序)
调整后:
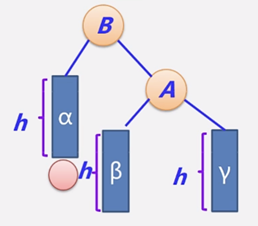
2)RR型:
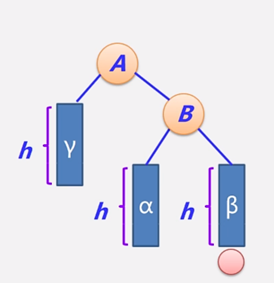
对于RR型失衡需要通过对根结点A进行左旋调整:
- 将 右子节点(B) 提升为新的根节点。
- 原根节点(A)成为 B 的左子节点。
- B 的原左子树(α)转移到 A 的右子树(保持二叉搜索树的顺序)
调整后:
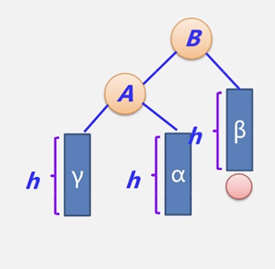
3)LR型:需要对其左子树进行左旋使其变成LL型,然后再进行右旋。
4)RL型:需要对其右子树进行右旋使其变成RR型,然后再进行左旋。
三、算法实现:
构建平衡二叉树的基本思想:在构建二叉排序树的过程中,每插入一个结点,先检查是否因插入而破坏了树的平衡性,若是,则找出最小不平衡树,对其进行调整,使其成为新的平衡子树。
首先是树结点结构:
struct TNode{
int BF; //增加一个平衡因子
int val;
TNode* lc;
TNode* rc;
TNode(int v):val(v),lc(NULL),rc(NULL),BF(0){}
};
接着是左旋和右旋的函数:
void R_Rotate(TNode* &root){ //右旋函数
TNode* x=root->lc;
TNode* y=x->rc;
x->rc=root;
root->lc=y;
root=x; //根结点指向x。
}
void L_Rotate(TNode* &root){ //左旋函数(与右旋相反)
TNode* x=root->rc;
TNode* y=x->lc;
x->lc=root;
root->rc=y;
root=x;
}
然后是处理最小不平衡子树的函数:
这个函数的关键是处理后相关结点的BF的计算,也是最难的一个点。
void LeftBalance(TNode* &root){ //调整左树过高 ,这个函数的关键是BF值的修改
TNode* x=root->lc;
TNode* y=x->rc;
if(x->BF==1){ //LL型
root->BF=0;
x->BF=0; //LL型调整过后root和x的BF都为0
R_Rotate(root);
}
else{ //这里x的BF为-1 (LR型)
switch(y->BF){
case 1:
root->BF = -1;
x->BF = 0;
break;
case 0:
root->BF =0;
x->BF = 0;
break;
case -1:
root->BF = 0;
x->BF = 1;
break;
}
y->BF = 0;
L_Rotate(root->lc);
R_Rotate(root);
}
}
void RightBalance(TNode* &root){ //和LeftBalance函数类似
TNode* x=root->rc;
TNode* y=x->lc;
if(x->BF==-1){
root->BF=0;
x->BF=0;
L_Rotate(root);
}
else{
switch(y->BF){
case 1:
root->BF=0;
x->BF=-1;
break;
case 0:
root->BF=0;
x->BF=0;
break;
case -1:
root->BF=1;
x->BF=0;
break;
}
y->BF=0;
R_Rotate(root->rc);
L_Rotate(root);
}
}
最后是插入函数:
插入函数在插入的同时需要判断其是否长高,如果长高就要判断其是否失衡,若失衡则要调用处理最小不平衡子树的函数来调整。
bool Insert_AVL(TNode* &root,int value,bool &higher){ //插入并构建平衡二叉树 higher:用来判断插入操作是否使树高度增加
if(!root){
root=new TNode(value);
higher=true;
return true;
}
else if(root->val==value)
return false;
else{
bool inserted=false;
if(value<root->val){
inserted=Insert_AVL(root->lc,value,higher);
if(inserted){
if(higher){
switch(root->BF){
case 1:
LeftBalance(root); //进行平衡调整过后higher变为false
higher=false;
break;
case 0:
root->BF=1;
higher=true; //左树长高,整体长高
break;
case -1:
root->BF=0; //原先右树高于左树,整体高度不变
higher=false;
break;
}
}
return true;
}
return false;
}
else{
inserted=Insert_AVL(root->rc,value,higher);
if(inserted){
if(higher){
switch(root->BF){
case 1:
root->BF=0;
higher=false;
break;
case 0:
root->BF=-1;
higher=true;
break;
case -1:
RightBalance(root);
higher=false;
break;
}
}
return true;
}
return false;
}
}
}
整体代码:
#include<iostream>
using namespace std;
struct TNode{
int BF; //增加一个平衡因子
int val;
TNode* lc;
TNode* rc;
TNode(int v):val(v),lc(NULL),rc(NULL),BF(0){}
};
void R_Rotate(TNode* &root){ //右旋函数
TNode* x=root->lc;
TNode* y=x->rc;
x->rc=root;
root->lc=y;
root=x; //根结点指向x。
}
void L_Rotate(TNode* &root){ //左旋函数(与右旋相反)
TNode* x=root->rc;
TNode* y=x->lc;
x->lc=root;
root->rc=y;
root=x;
}
void LeftBalance(TNode* &root){ //调整左树过高 ,这个函数的关键是BF值的修改
TNode* x=root->lc;
TNode* y=x->rc;
if(x->BF==1){
root->BF=0;
x->BF=0; //LL型调整过后root和x的BF都为0
R_Rotate(root);
}
else{ //这里x的BF为-1
switch(y->BF){
case 1:
root->BF = -1;
x->BF = 0;
break;
case 0:
root->BF =0;
x->BF = 0;
break;
case -1:
root->BF = 0;
x->BF = 1;
break;
}
y->BF = 0;
L_Rotate(root->lc);
R_Rotate(root);
}
}
void RightBalance(TNode* &root){ //和LeftBalance函数类似
TNode* x=root->rc;
TNode* y=x->lc;
if(x->BF==-1){
root->BF=0;
x->BF=0;
L_Rotate(root);
}
else{
switch(y->BF){
case 1:
root->BF=0;
x->BF=-1;
break;
case 0:
root->BF=0;
x->BF=0;
break;
case -1:
root->BF=1;
x->BF=0;
break;
}
y->BF=0;
R_Rotate(root->rc);
L_Rotate(root);
}
}
bool Insert_AVL(TNode* &root,int value,bool &higher){ //插入并构建平衡二叉树 higher:用来判断插入操作是否使树高度增加
if(!root){
root=new TNode(value);
higher=true;
return true;
}
else if(root->val==value)
return false;
else{
bool inserted=false;
if(value<root->val){
inserted=Insert_AVL(root->lc,value,higher);
if(inserted){
if(higher){
switch(root->BF){
case 1:
LeftBalance(root); //进行平衡调整过后higher变为false
higher=false;
break;
case 0:
root->BF=1;
higher=true; //左树长高,整体长高
break;
case -1:
root->BF=0; //原先右树高于左树,整体高度不变
higher=false;
break;
}
}
return true;
}
return false;
}
else{
inserted=Insert_AVL(root->rc,value,higher);
if(inserted){
if(higher){
switch(root->BF){
case 1:
root->BF=0;
higher=false;
break;
case 0:
root->BF=-1;
higher=true;
break;
case -1:
RightBalance(root);
higher=false;
break;
}
}
return true;
}
return false;
}
}
}
void preOrder(TNode* root){ //前序遍历
if(!root)
return;
else{
cout<<root->val<<" ";
preOrder(root->lc);
preOrder(root->rc);
}
}
// 释放内存
void DestroyTree(TNode* root) {
if(root) {
DestroyTree(root->lc);
DestroyTree(root->rc);
delete root;
}
}
int main(){
int value;
int n,i;
TNode* root=NULL;
bool higher=false;
cin>>n;
for(i=0;i<n;i++){
cin>>value;
Insert_AVL(root,value,higher);
}
preOrder(root);
DestroyTree(root);
return 0;
}
运行结果:
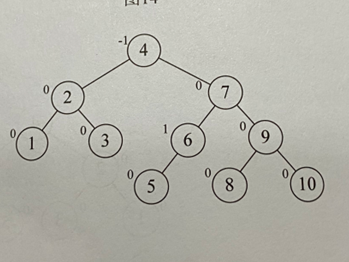
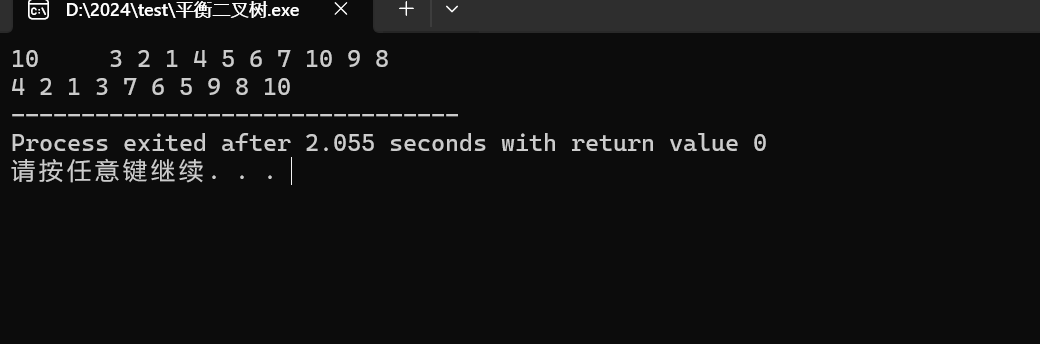




















 4800
4800

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








