一、简单选择排序:每一轮从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
struct SqList{
int *r; //用于存储要排序的数组,大小是数字个数+1,其中r[0]用作哨兵,目的是减小时间复杂度
int length; //记录数字个数
};
void swap(SqList &L,int i,int j){
int temp=L.r[i];
L.r[i]=L.r[j];
L.r[j]=temp;
}
void SelectSort(SqList &L){
int i,j,k;
for(i=1;i<L.length;i++){
k=i;
for(j=i+1;j<=L.length;j++){
if(L.r[j]<L.r[k])
k=j;
}
if(k!=i)
swap(L,i,k);
}
}
二、堆排序
1、堆:1)父结点与子节点存在特定的大小关系
- 大顶堆:每个父节点的值 大于等于 其左右子节点的值
- 小顶堆:每个父节点的值 小于等于 其左右子节点的值
2)是完全二叉树
2、完全二叉树结构
堆的物理存储通常使用数组实现(逻辑上是二叉树),对于数组中索引为 i 的节点
- 左子节点索引为
2*i - 右子节点索引为
2*i + 1 - 父节点索引为
i/2(向下取整)
完全二叉树的最大父节点的索引为n/2。(n为数组元素个数)
3、堆排序算法:
- 1):构建大顶堆
将无序数组转换为大顶堆,此时堆顶元素(根节点)是数组的最大值。 - 2):交换与调整
- 将堆顶元素(最大值)与堆的最后一个元素交换,最大值被放到数组末尾。
- 排除已排序的末尾元素,对剩余元素重新调整为大顶堆,继续选出剩余部分的最大值。
- 重复上述过程,直到整个数组有序。
//已知L.r[s..m]除了关键字L.r[s]其他的均满足堆的定义
//函数作用:将以i为顶,m为末尾的堆变为大顶堆
void HeapAdjust(SqList &L,int s,int m){
int i,temp;
temp=L.r[s];
for(i=2*s;i<=m;i*=2){
if(i<m&&L.r[i]<L.r[i+1])
i++;
if(temp>L.r[i])
break;
L.r[s]=L.r[i];
s=i;
}
L.r[s]=temp;
}
void HeapSort(SqList &L){
int i,j;
for(i=L.length/2;i>=1;i--){ //构建大顶堆
HeapAdjust(L,i,L.length);
}
for(i=L.length;i>1;i--){ //交换与调整
swap(L,1,i);
HeapAdjust(L,1,i-1);
}
}
完整代码:
#include<iostream>
using namespace std;
struct SqList{
int *r; //用于存储要排序的数组,大小是数字个数+1,其中r[0]用作哨兵,目的是减小时间复杂度
int length; //记录数字个数
};
void swap(SqList &L,int i,int j){
int temp=L.r[i];
L.r[i]=L.r[j];
L.r[j]=temp;
}
//已知L.r[s..m]除了关键字L.r[s]其他的均满足堆的定义
//函数作用:将以i为顶,m为末尾的堆变为大顶堆
void HeapAdjust(SqList &L,int s,int m){
int i,temp;
temp=L.r[s];
for(i=2*s;i<=m;i*=2){
if(i<m&&L.r[i]<L.r[i+1])
i++;
if(temp>L.r[i])
break;
L.r[s]=L.r[i];
s=i;
}
L.r[s]=temp;
}
void HeapSort(SqList &L){
int i,j;
for(i=L.length/2;i>=1;i--){ //构建大顶堆
HeapAdjust(L,i,L.length);
}
for(i=L.length;i>1;i--){ //交换与调整
swap(L,1,i);
HeapAdjust(L,1,i-1);
}
}
int main(){
int n,i;
SqList L;
cin>>n;
L.r=new int[n+1];
L.length=n;
for(i=1;i<n+1;i++){
cin>>L.r[i];
}
HeapSort(L);
for(i=1;i<=L.length;i++){
cout<<L.r[i]<<" ";
}
cout<<endl;
delete[] L.r; // 释放动态分配的内存
return 0;
}
三、归并排序:利用分治法的思想实现的排序
下面我们使用非递归的算法来实现归并排序:
基本思路:
-
自底向上的合并策略:
- 初始子数组长度为 1:直接将每个元素视为有序子数组。
- 逐层合并:
- 第一轮:合并相邻的长度为 1 的子数组(如
[5]和[3]→[3,5])。 - 第二轮:合并相邻的长度为 2 的子数组(如
[3,5]和[4,8]→[3,4,5,8])。 - 重复此过程,直到子数组长度覆盖整个数组。
- 第一轮:合并相邻的长度为 1 的子数组(如
-
交替使用原数组和临时数组:
- 通过两次
MergePass交替操作:- 第一次将原数组
L.r的数据归并到临时数组TR。 - 第二次将临时数组
TR的数据归并回原数组L.r。
- 第一次将原数组
- 每次归并后,子数组长度翻倍(
s *= 2),确保覆盖更大的范围。
- 通过两次
参考代码:
void MergeSort(SqList &L){
int s=1;
int *TR=new int[L.length+1];
while(s<L.length){
MergePass(L.r,TR,s,L.length);
s*=2;
MergePass(TR,L.r,s,L.length); //这里使用两次是为了避免在MergePass中重复拷贝
s*=2;
}
}
void MergePass(int *SR,int *TR,int s,int n){ //将SR[]中相邻长度为s的子序列两两归并到TR[]中
int i=1;
int j;
while(i<n-2*s+1){
MSort(SR,TR,i,i+s-1,i+2*s-1);
i+=2*s;
}
if(i<n-s+1){
MSort(SR,TR,i,i+s-1,n);
}
else{
for(j=i;j<=n;j++){
TR[j]=SR[j];
}
}
}
MSort(int *SR,int *TR,int s,int m,int l){ //将SR中起点为s,中点为m,终点为l的子序列进行归并排序
int i=s,j=m+1;
int k=s;
while(i<=m&&j<=l){
if(SR[i]<SR[j]){
TR[k]=SR[i];
i++;
k++;
}
else{
TR[k]=SR[j];
j++;
k++;
}
}
while(i<=m){
TR[k]=SR[i];
i++;
k++;
}
while(j<=l){
TR[k]=SR[j];
j++;
k++;
}
}
四、不同排序算法的比较:
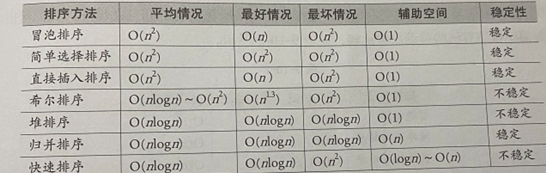
 选择排序、堆排序与归并排序算法解析
选择排序、堆排序与归并排序算法解析





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








