图的存储结构

 1、邻接矩阵：用两个数组来表示图，一个一维数组存储图中顶点信息，一个二维数组（邻接矩阵）存储图中边或弧的信息。

图的邻接矩阵存储及度计算：

#include<iostream>
#include<vector>
using namespace std;
struct MGraph{
	vector<char>vex;
	vector<vector<int> >arc;//存储边的二维数组
	MGraph(int n){
		vex.resize(n);
		arc.resize(n);
		int i;
		for(i=0;i<n;i++){
			arc[i].resize(n);
		}
	}
};
int findPos(vector<char>vex,char v){
	int n=vex.size();
	int i;
	for(i=0;i<n;i++){
		if(vex[i]==v)
		    return i;
	}
	return -1;
}
void creatDGraph(MGraph& gp,int n){//创建有向图 
	int i;
	for(i=0;i<n;i++){
		cin>>gp.vex[i];
	}
	int e;//表示边数
	cin>>e;
	for(i=0;i<e;i++){
		char v1,v2;
		cin>>v1>>v2;
		int M=findPos(gp.vex,v1);
		int N=findPos(gp.vex,v2);
		if(M>=0&&N>=0){
			gp.arc[M][N]=1;
		}
	} 
}
void creatUGraph(MGraph& gp,int n){//创建无向图 
	int i;
	for(i=0;i<n;i++){
		cin>>gp.vex[i];
	}
	int e;//表示边数
	cin>>e;
	for(i=0;i<e;i++){
		char v1,v2;
		cin>>v1>>v2;
		int M=findPos(gp.vex,v1);
		int N=findPos(gp.vex,v2);
		if(M>=0&&N>=0){
			gp.arc[M][N]=1;
			gp.arc[N][M]=1;//对称矩阵 
		}
	} 
}
void getDDegree(MGraph& gp){//获取有向图的度
	int i,j;
	int n=gp.vex.size();
	for(i=0;i<n;i++){
		cout<<gp.vex[i]<<": ";
		int count1=0,count2=0;//count1表示出度，count2表示入度 
		for(j=0;j<n;j++){
			if(gp.arc[i][j]==1)
			    count1++;
			if(gp.arc[j][i]==1)
			    count2++;
		}
		cout<<count1<<" "<<count2<<" "<<count1+count2<<endl;
	}
}
void getUDegree(MGraph& gp){获取无向图的图
	int i,j;
	int n=gp.vex.size();
	for(i=0;i<n;i++){
		cout<<gp.vex[i]<<": ";
		int count=0;
		for(j=0;j<n;j++){
			if(gp.arc[i][j]==1)
			    count++;
			
		}
		cout<<count<<endl;
	}
}
int main(){
	int T;
	cin>>T;
	while(T--){
		char type;//图类型：D—有向图，U—无向图
		int n;//顶点数 
		cin>>type>>n;
		MGraph gp(n);
		if(type=='D'){
			creatDGraph(gp,n);
			getDDegree(gp);
		}
		else if(type=='U'){
			creatUGraph(gp,n);
			getUDegree(gp);
		}    	
	}
	return 0;
} 

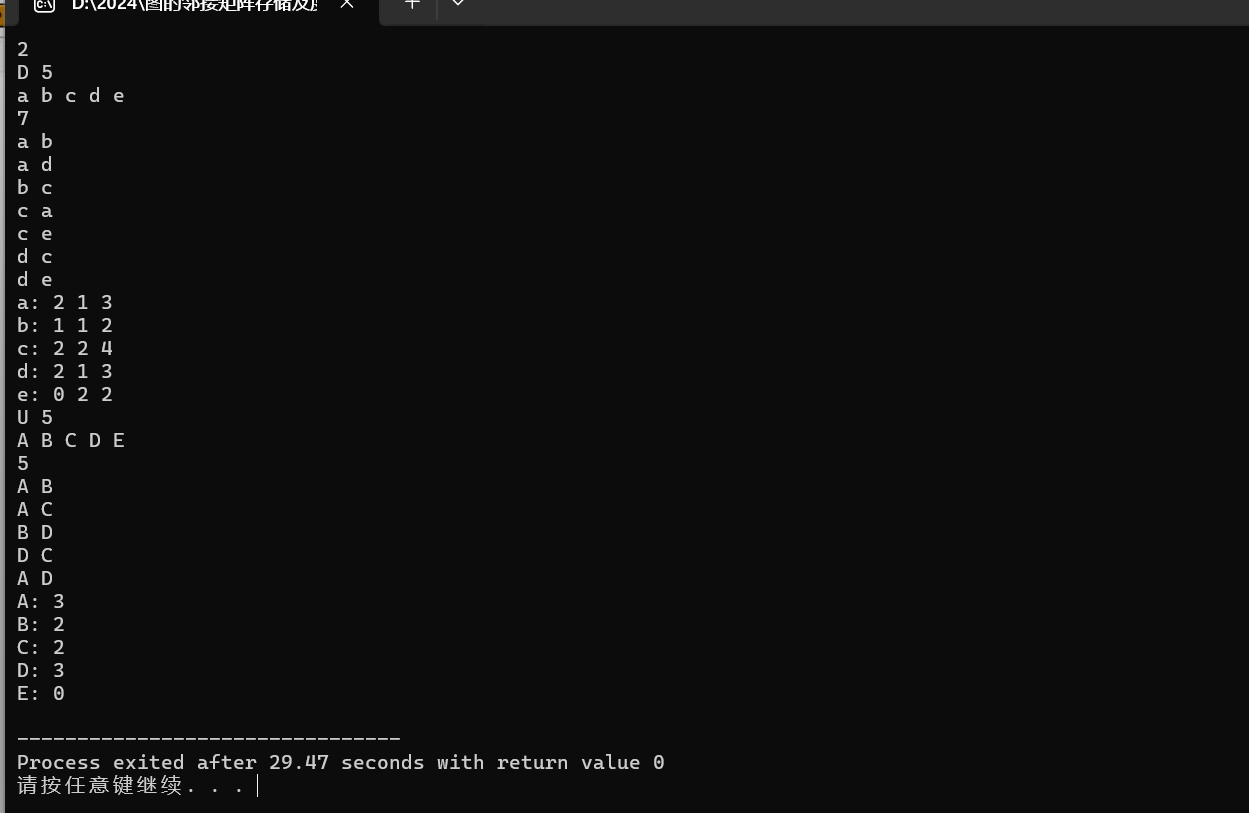
 输入输出案例如下：

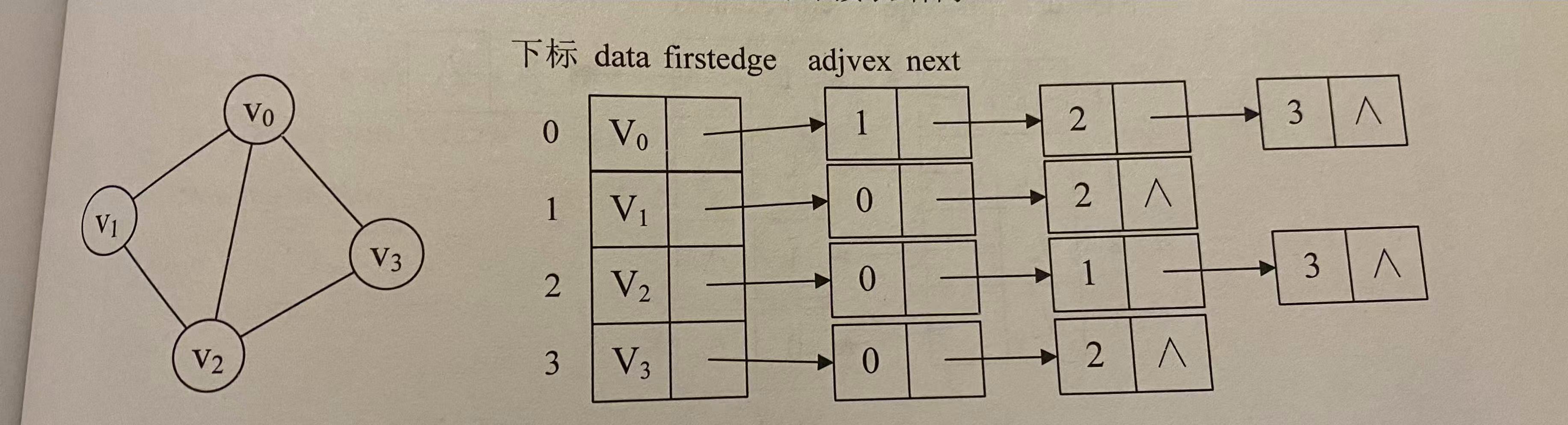
2、邻接表：数组与链表结合的存储方法

eg:下图为无向图的邻接表结构

构建有向邻接表：

​
#include<iostream>
#include<vector>
#include<list>
using namespace std;

struct vertex{
	char vexc;//表示顶点字符 
	list<int>vexl;//表示与顶点相连通的点在顶点数组中的坐标 
};
struct LGraph{//LGraph表示邻接表构成的图(list) 
	vector<vertex>vex;
	LGraph(int n){
		vex.resize(n);	
	}
}; 
int findPos(LGraph lg,char vn){
	int n=lg.vex.size();
	int i;
	for(i=0;i<n;i++){
		if(lg.vex[i].vexc==vn)
		    return i;
	}
	return -1;
}
void creatLGraph(LGraph& lg,int n,int k){
	int i;
	for(i=0;i<n;i++){
		cin>>lg.vex[i].vexc;
	}
	for(i=0;i<k;i++){
		char v1,v2;
		cin>>v1>>v2;
		int M=findPos(lg,v1);
		int N=findPos(lg,v2);
		if(M>=0&&N>=0)
		    lg.vex[M].vexl.push_back(N);
	}
}
void showLGraph(const LGraph&lg){
	int i;
	int n=lg.vex.size();
	for(i=0;i<n;i++){
		cout<<i<<" "<<lg.vex[i].vexc;
		list<int>::const_iterator it=lg.vex[i].vexl.begin();
		while(it != lg.vex[i].vexl.end()){ 
			cout<<'-'<<*it;
			it++;
		}
		cout<<"-^"<<endl;
	}
}
int main(){
	int t;
	cin>>t;
	while(t--){
		int n,k;//n表示顶点数,k表示弧数 
		cin>>n>>k;
		LGraph lg(n);
		creatLGraph(lg,n,k);
		showLGraph(lg);
	}
	
	return 0;
} 

​

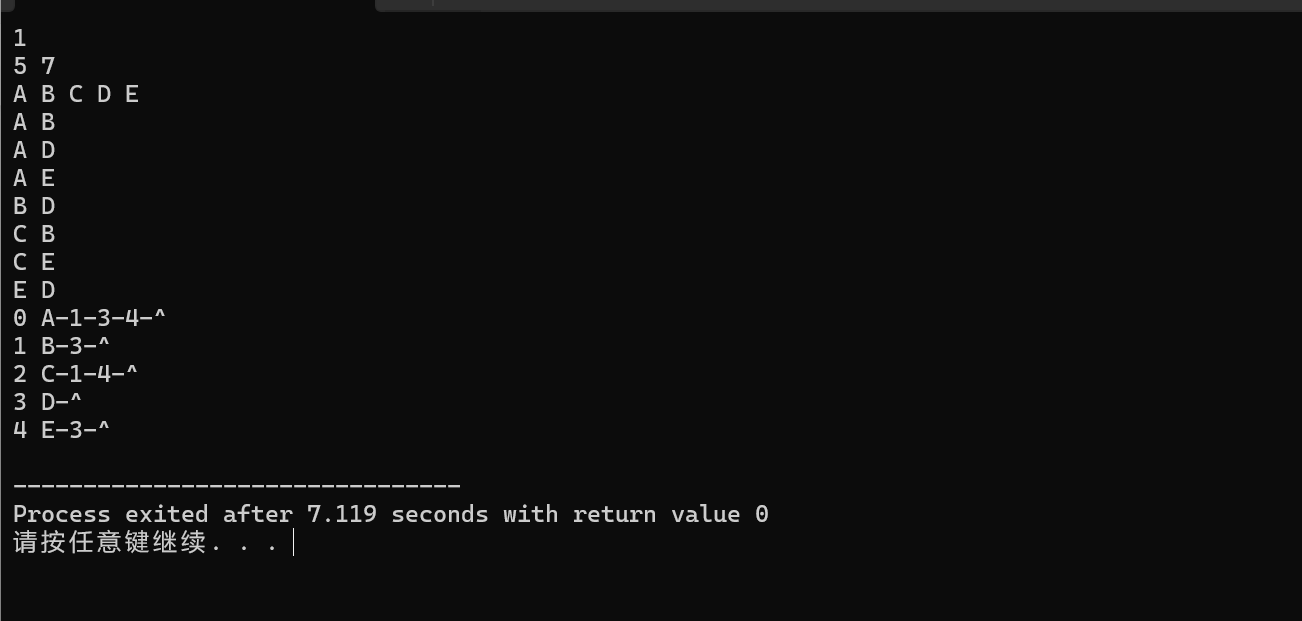
输入输出案例如下