最小生成树（Prim算法和Kruskal算法）-优快云博客

本文链接：https://blog.youkuaiyun.com/Yuking_Go/article/details/148631227

1、生成树：没有回路的图，即一个有n个顶点的生成树只有n-1条通路。

最小生成树：构造连通网的最小代价生成树。

2、Prim算法：构造最小生成树的一种算法，普里姆算法的基本思想是从一个起始顶点开始，逐步扩展生成树，直到包含所有顶点。具体步骤如下：

1. 初始化一个空的生成树。
2. 选择一个起始顶点，将其加入生成树中。
3. 在生成树与非生成树的边中选择权值最小的边，将其加入生成树中。
4. 重复第三步，直到生成树包含所有顶点。

下面以邻接矩阵构成的图进行Prim算法示范：

#include<iostream>
#include<vector>
using namespace std;
struct MGraph{
	vector<char>vex;
	vector<vector<int> >arc;//存储边的二维数组
	MGraph(int n){
		vex.resize(n);
		arc.resize(n);
		int i;
		for(i=0;i<n;i++){
			arc[i].resize(n);
		}
	}
};
struct MCST{//最小生成树结构体 
	vector<pair<char,char> >road;
	vector<int>weight; 
};
int findPos(vector<char>vex,char v){
	int n=vex.size();
	int i;
	for(i=0;i<n;i++){
		if(vex[i]==v)
		    return i;
	}
	return -1;
}

void creatUGraph(MGraph& gp,int n){//创建无向图 
	int i,j;
	for(i=0;i<n;i++){
		cin>>gp.vex[i];
	}
	int e;//表示边数
	cin>>e;
	for(i=0;i<n;i++){
		for(j=0;j<n;j++){
			gp.arc[i][j]=0x7FFFFFFF;
		}
	}
	for(i=0;i<e;i++){
		char v1,v2;
		int w;
		cin>>v1>>v2>>w;
		int M=findPos(gp.vex,v1);
		int N=findPos(gp.vex,v2);
		if(M>=0&&N>=0){
			gp.arc[M][N]=w;
			gp.arc[N][M]=w;//对称矩阵 
		}
	} 
}
MCST creatMCST(const MGraph&gp){
	int n=gp.vex.size();
	vector<bool> visited(n,false);//用来标记顶点是否在最小连通树中 
	MCST mt;
	int i,j,k;
    char start;//选择第一个结点 
    cin>>start;
    if(findPos(gp.vex,start)!=-1)
        visited[findPos(gp.vex,start)]=true;//找到第一个顶点的位置并将该点的visited标记为true 

	for(i=0;i<n-1;i++){
		int min=0x7FFFFFFF;
		int from=-1,to=-1;
		for(j=0;j<n;j++){   //在生成树与非生成树的边中选择权值最小的边
			if(visited[j]){    
				for(k=0;k<n;k++){
					if(!visited[k]&&gp.arc[j][k]<min){
						min=gp.arc[j][k];
						from=j;
						to=k;
					}
				}
			}		
		}
		if(from!=-1&&to!=-1){
			visited[to]=true;
			mt.road.push_back({gp.vex[from],gp.vex[to]});
			mt.weight.push_back(min);
		}
	}
	return mt;
}
void showMCST(const MCST&mt){//输出最小生成树 
	int n=mt.road.size();
	int sum_weight=0;
	int i;
	for(i=0;i<n;i++){
		sum_weight+=mt.weight[i];
	}
	cout<<sum_weight<<endl;
	for(i=0;i<n;i++){
		cout<<mt.road[i].first<<" "<<mt.road[i].second<<" "<<mt.weight[i]<<endl;
	}
}
int main(){
		int n;//顶点数 
		cin>>n;
		MGraph gp(n);
		creatUGraph(gp,n); 
	    MCST mt= creatMCST(gp);
	    showMCST(mt);
	return 0;
}

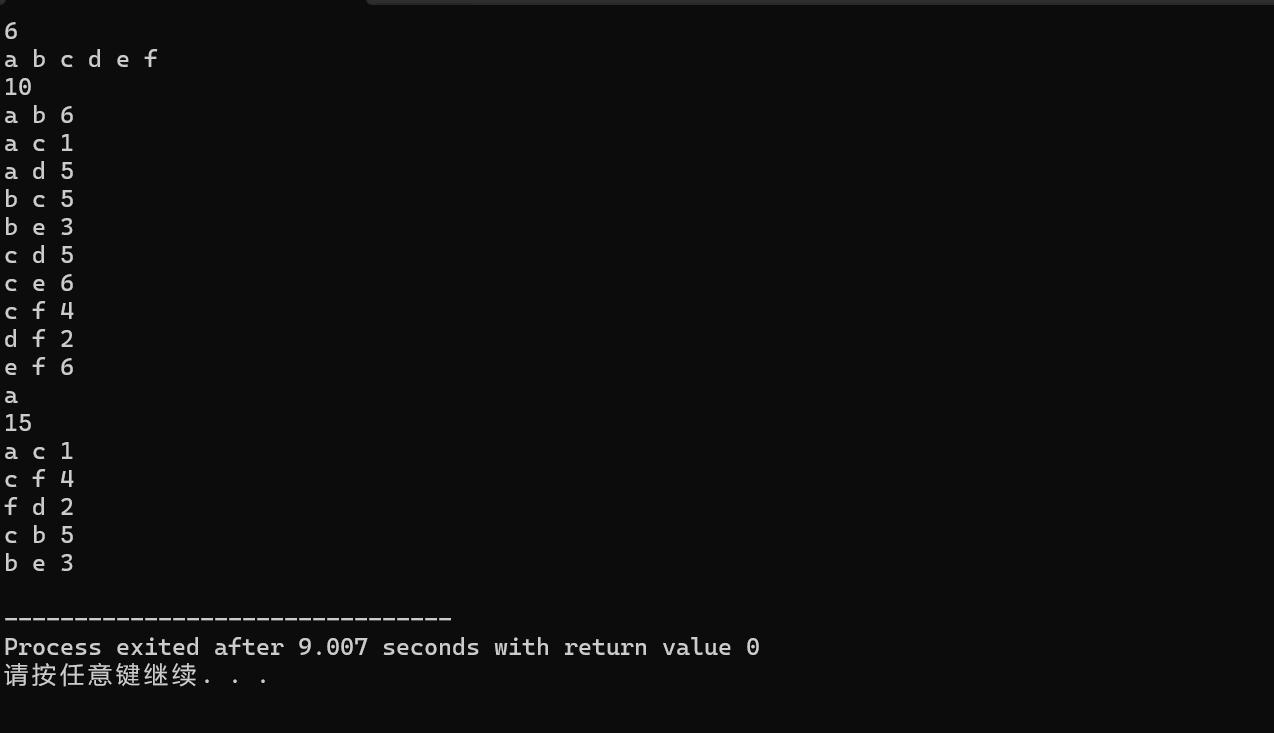
输入输出如下：

3，Kruskal算法：基本思路是：
1将图中所有边按权重从小到大排序
2依次选择权重最小的边，如果该边不会与已选择的边形成环路，则加入最小生成树
3重复步骤 2，直到选择了 n-1 条边

算法的核心是通过parent数组将不连通的图转化为不同的树，通过检查根节点是否相同从而实现连通性检查。

#include<iostream>
#include<vector>
#include<algorithm> 
using namespace std;
struct MGraph{
	vector<char>vex;
	vector<vector<int> >arc;//存储边的二维数组
	MGraph(int n){
		vex.resize(n);
		arc.resize(n);
		int i;
		for(i=0;i<n;i++){
			arc[i].resize(n);
		}
	}
};
struct edge{//用edge结构体来存储边 
	int from;
	int to;
	int weight;
	edge(int f,int t,int w):from(f),to(t),weight(w){
	}
	bool operator<(const edge&other){
		return (weight<other.weight);
	}
};
struct MCST{//最小生成树结构体 
	vector<pair<char,char> >road;
	vector<int>weight; 
};
int findPos(vector<char>vex,char v){
	int n=vex.size();
	int i;
	for(i=0;i<n;i++){
		if(vex[i]==v)
		    return i;
	}
	return -1;
}

void creatUGraph(MGraph& gp,int n){//创建无向图 
	int i,j;
	for(i=0;i<n;i++){
		cin>>gp.vex[i];
	}
	int e;//表示边数
	cin>>e;
	for(i=0;i<n;i++){
		for(j=0;j<n;j++){
			gp.arc[i][j]=0x7FFFFFFF;
		}
	}
	for(i=0;i<e;i++){
		char v1,v2;
		int w;
		cin>>v1>>v2>>w;
		int M=findPos(gp.vex,v1);
		int N=findPos(gp.vex,v2);
		if(M>=0&&N>=0){
			gp.arc[M][N]=w;
			gp.arc[N][M]=w;//对称矩阵 
		}
	} 
}
int find(vector<int>&parent,int x){
	if(parent[x]!=x)
	    parent[x]=find(parent,parent[x]);  //通过递归找到根结点并赋值给 parent[x]
	                                        //路径压缩，方便后续查找
	return parent[x];                       
}

MCST Kruskal_MCST(const MGraph&gp){
	int n=gp.vex.size();
	MCST mt;
	vector<edge>ed;//构造一个edge型的vector容器来存储边 ，方便后续进行排序 
	int i,j;
	for(i=0;i<n;i++){//将边存入ed中 
		for(j=i+1;j<n;j++){
			if(gp.arc[i][j]!=0x7FFFFFFF){
				ed.push_back(edge(i,j,gp.arc[i][j]));	
			}
		}
	}
	sort(ed.begin(),ed.end());//对ed进行排序
	vector<int>parent(n);     //构造parent 
	for(i=0;i<n;i++){
		parent[i]=i;
	} 
	vector<edge>::iterator it=ed.begin();
	for(i=0;i<n-1;i++){
		while(1){
			int x=find(parent,it->from);
			int y=find(parent,it->to);
			if(x!=y){
				mt.road.push_back({gp.vex[it->from],gp.vex[it->to]});
				mt.weight.push_back(gp.arc[it->from][it->to]);
				parent[it->to]=find(parent,it->from);//将两个最小生成树导通 
				it++;
				break;
			}
			if(x==y){
				it++; 
				continue;
			}
		}
	} 
	return mt;	
}
void showMCST(const MCST&mt){//输出最小生成树 
	int n=mt.road.size();
	int sum_weight=0;
	int i;
	for(i=0;i<n;i++){
		sum_weight+=mt.weight[i];
	}
	cout<<sum_weight<<endl;
	for(i=0;i<n;i++){
		cout<<mt.road[i].first<<" "<<mt.road[i].second<<" "<<mt.weight[i]<<endl;
	}
}
int main(){
		int n;//顶点数 
		cin>>n;
		MGraph gp(n);
		creatUGraph(gp,n); 
	    MCST mt= Kruskal_MCST(gp);
	    showMCST(mt);
	return 0;
}

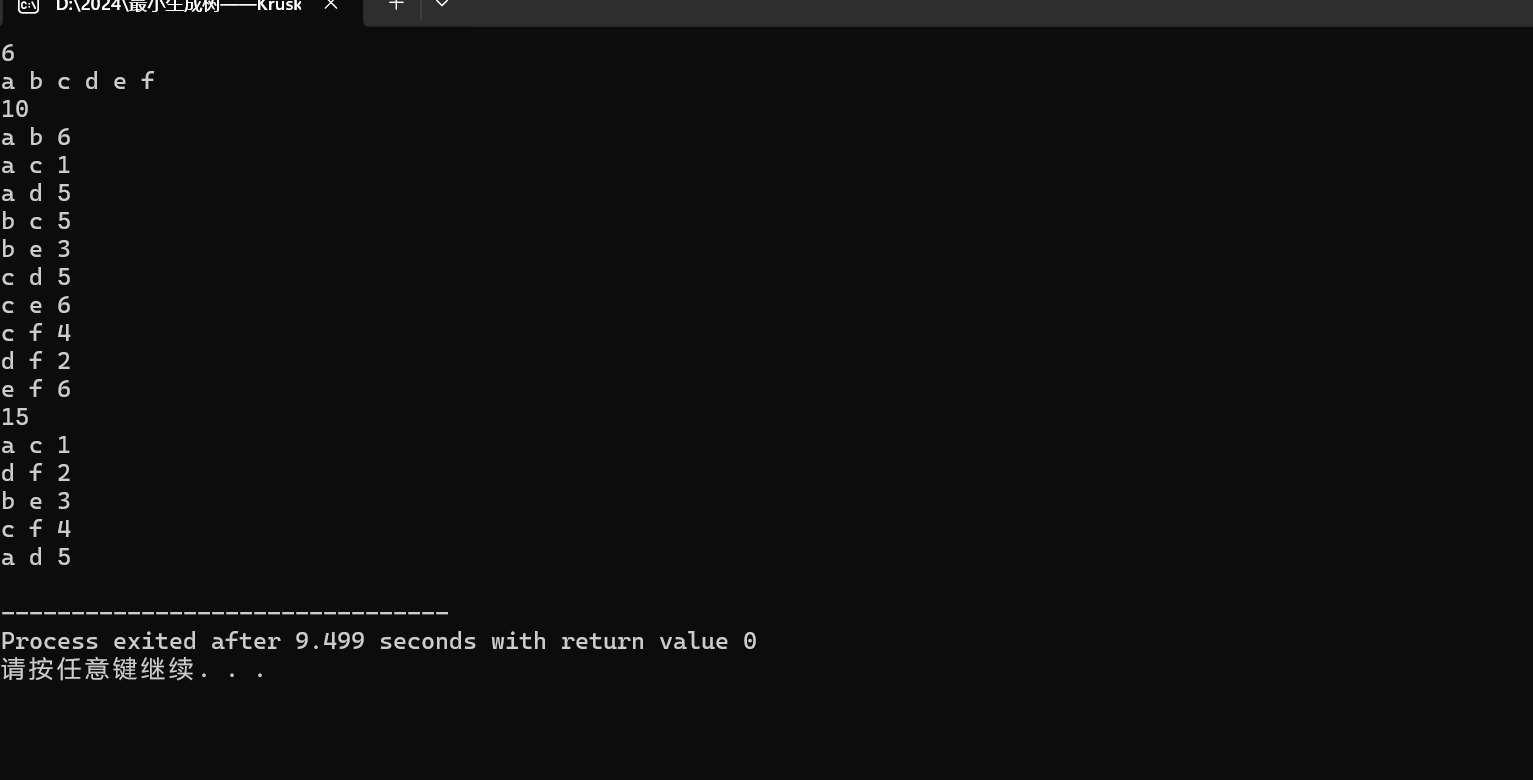
输入输出如下：