一探锁相环：模拟系统与数字系统

说明

本次实验探究的是输入信号与NCO本征频率一致的情况

一、模拟系统仿真结果（SystemView）

数据规格

Fs=8000Hz  样点数14501

Filter

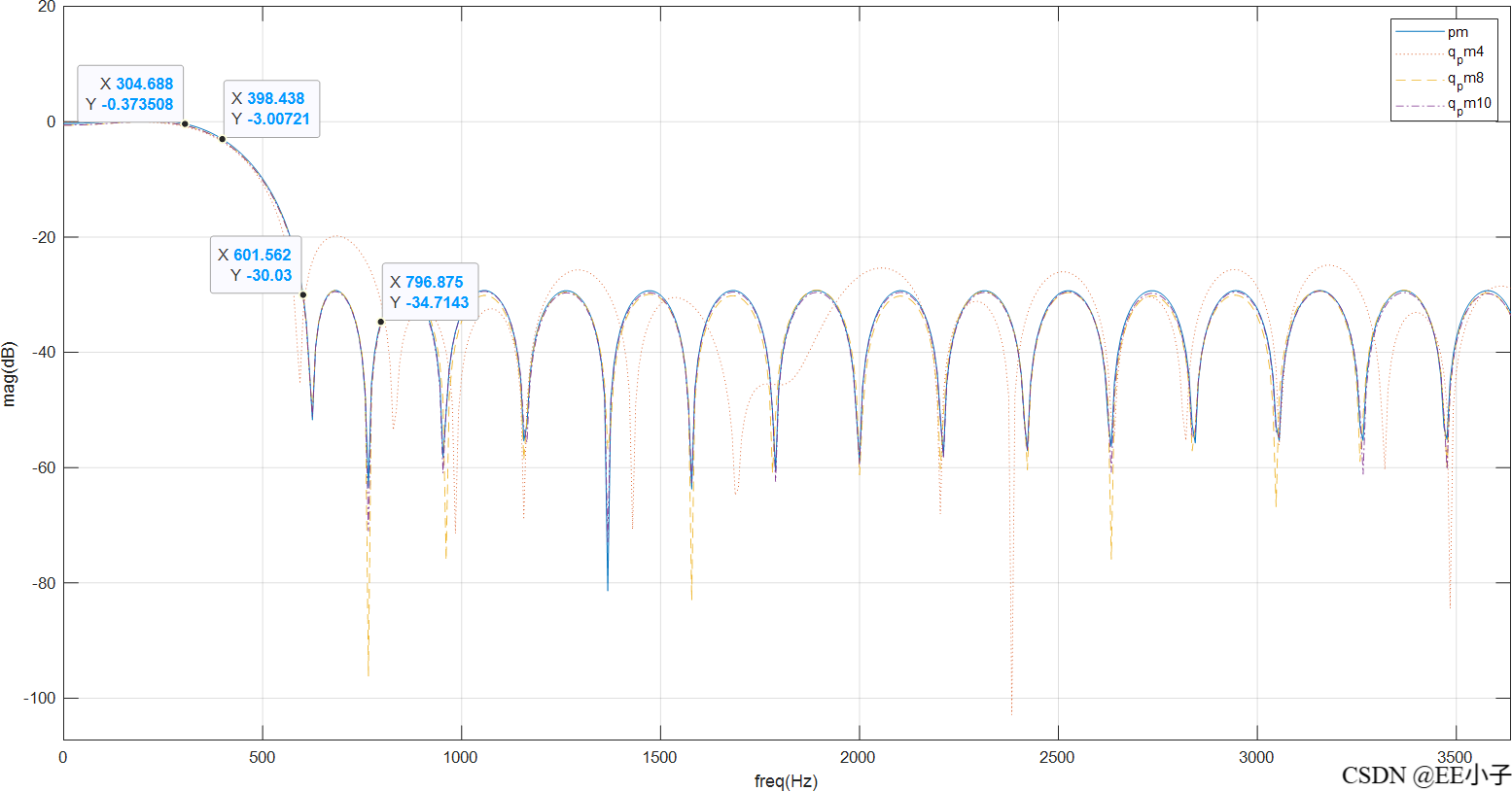
mult_out

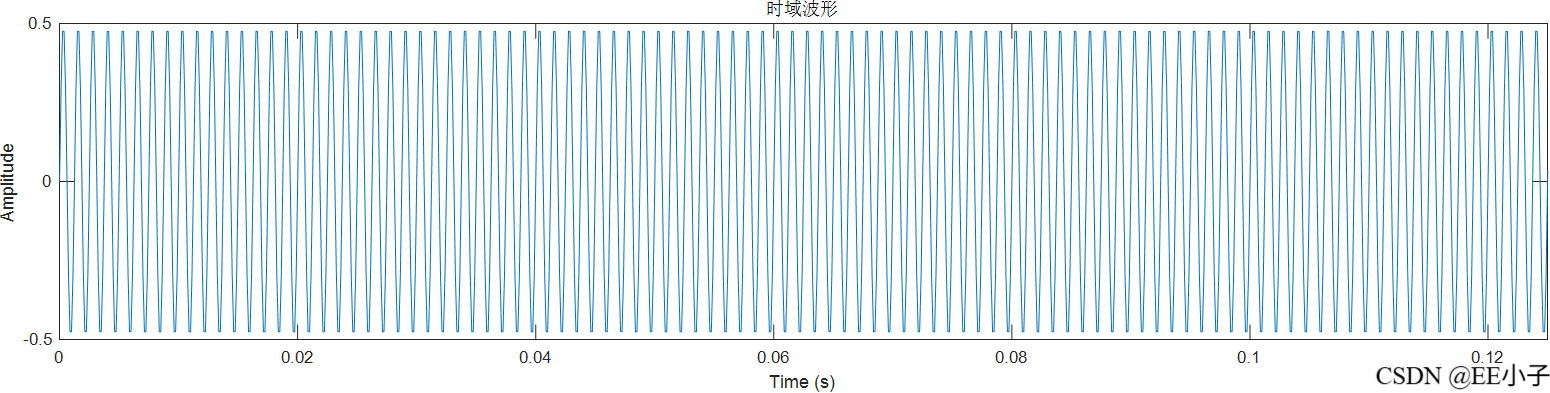
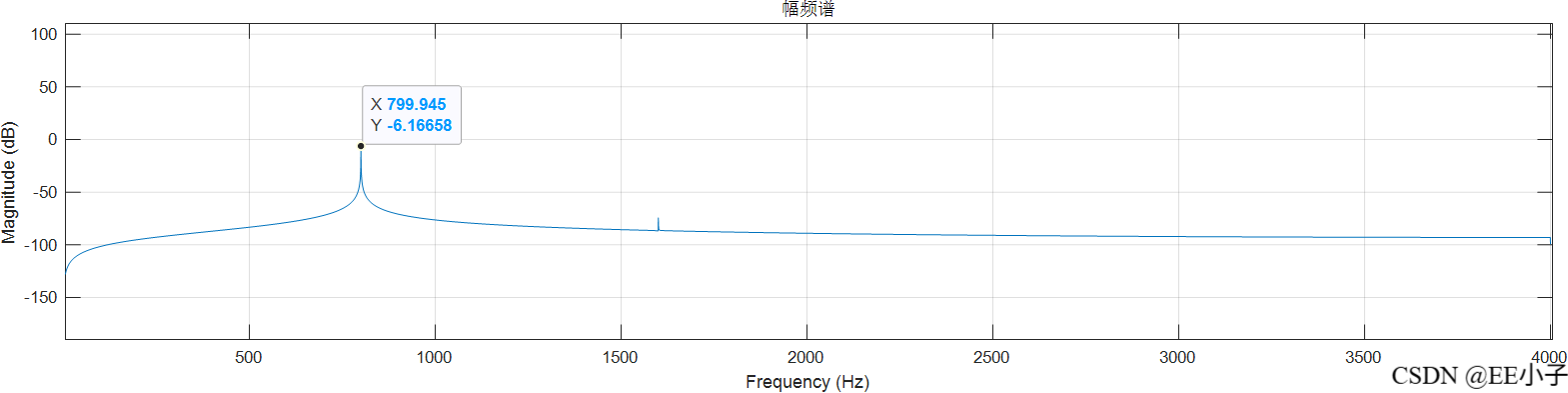
filter_out

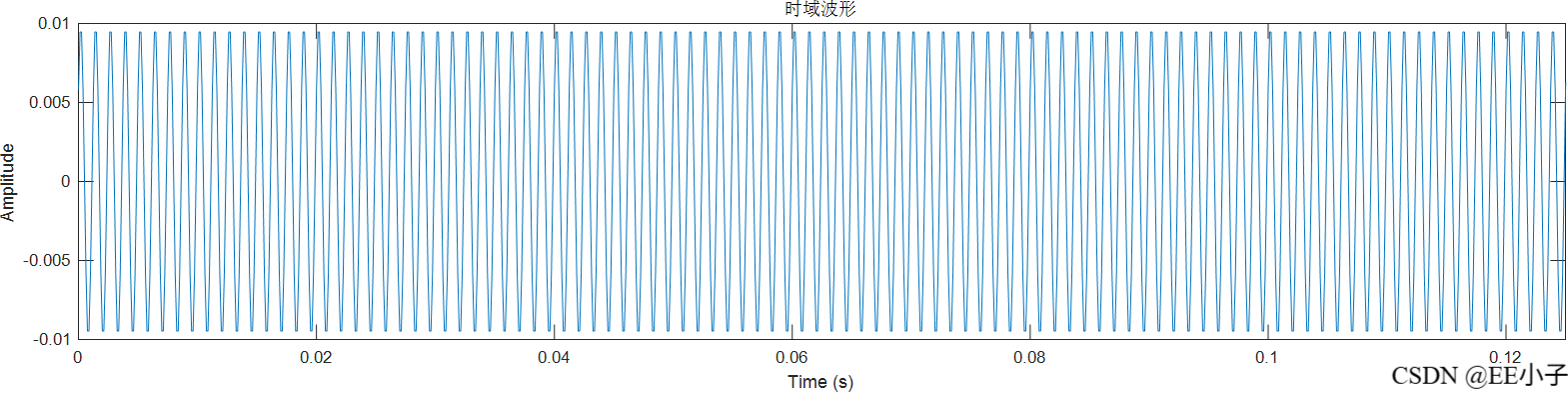
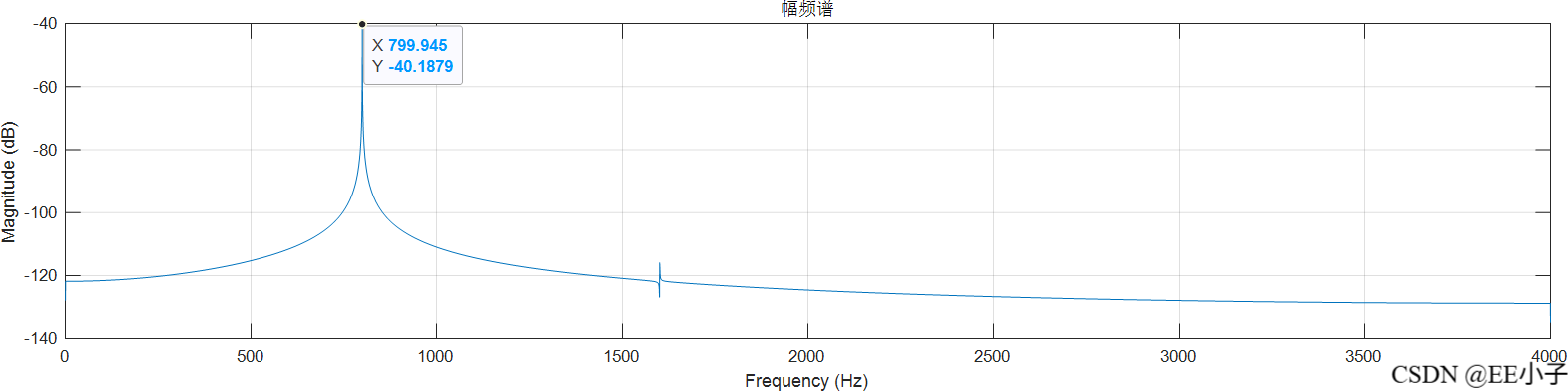
dout

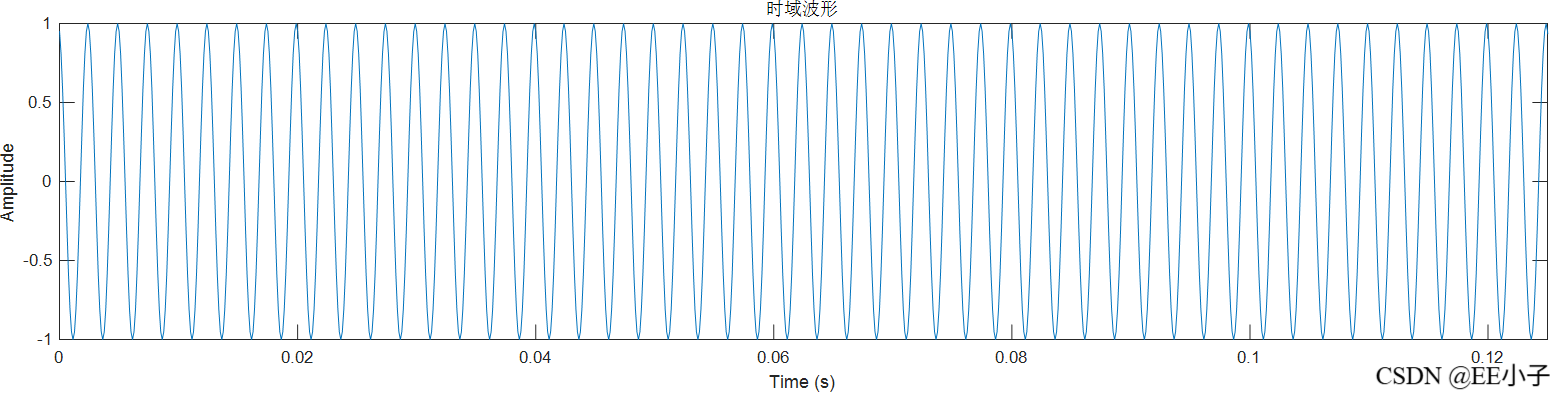
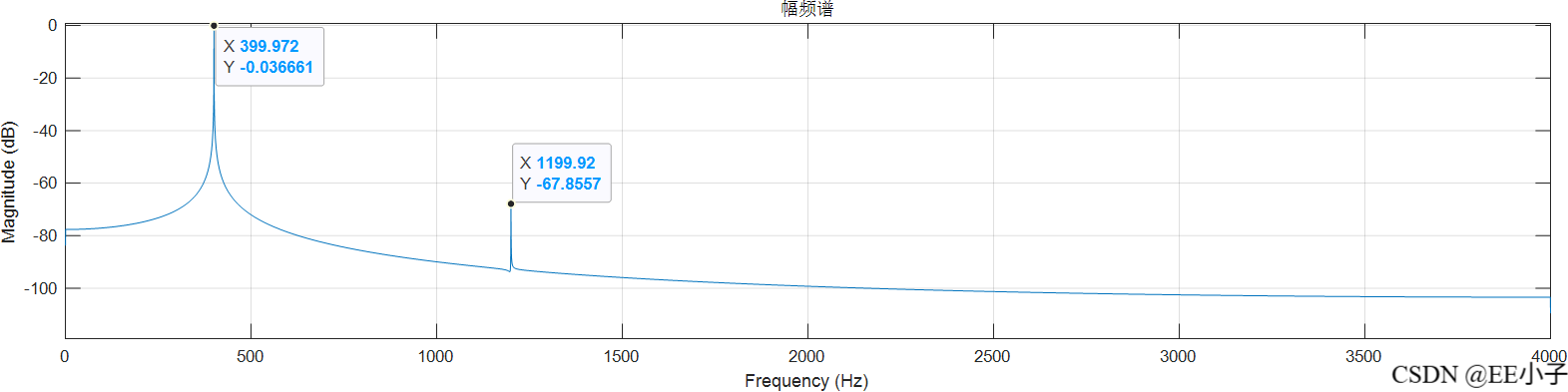
二、数字系统一仿真（Quartus+Modelsim）

实验参数

400Hz输入信号,19bit乘法器

乘法器输入10bits,10bits,输出20bits，pipeline 1

滤波器规格（pipeline=1）

Name	Direction	Width
clk	INPUT	1
reset_n	INPUT	1
ast_sink_data	INPUT	19
ast_source_data	OUTPUT	30
ast_sink_valid	INPUT	1
ast_sink_ready	OUTPUT	1
ast_source_valid	OUTPUT	1
ast_source_ready	INPUT	1
ast_sink_error	INPUT	2
ast_source_error	OUTPUT	2

NCO规格（Generation Algorithm : CORDIC）

Name	Direction	Width
phi_inc_i	INPUT	35
fsin_o	OUTPUT	10
fcos_o	OUTPUT	10
clk	INPUT	1
reset_n	INPUT	1
clken	INPUT	1
out_valid	OUTPUT	1
freq_mod_i	INPUT	30

实验结果

filter

mult_out

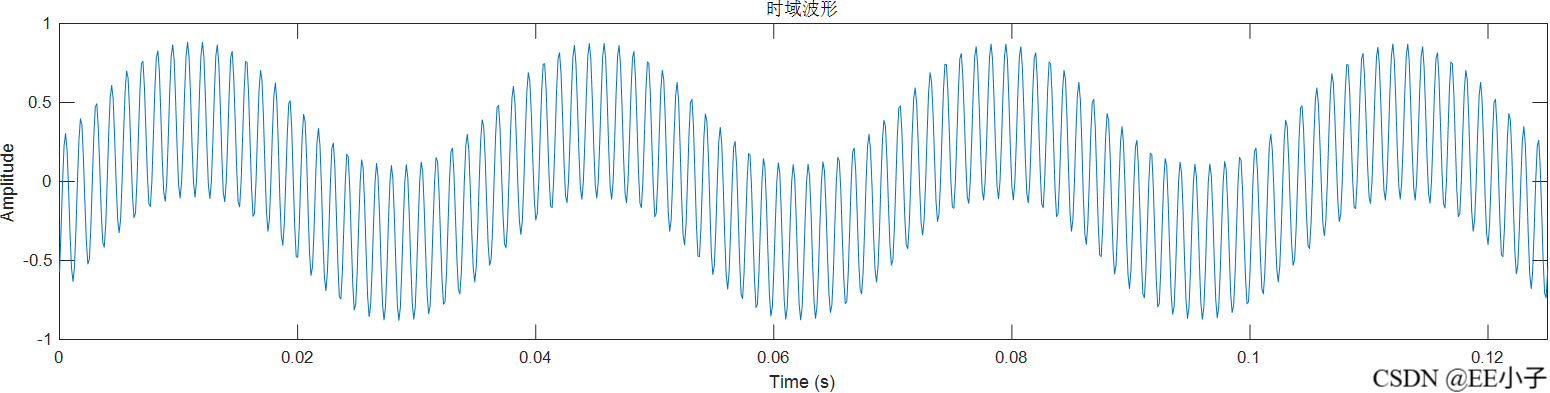
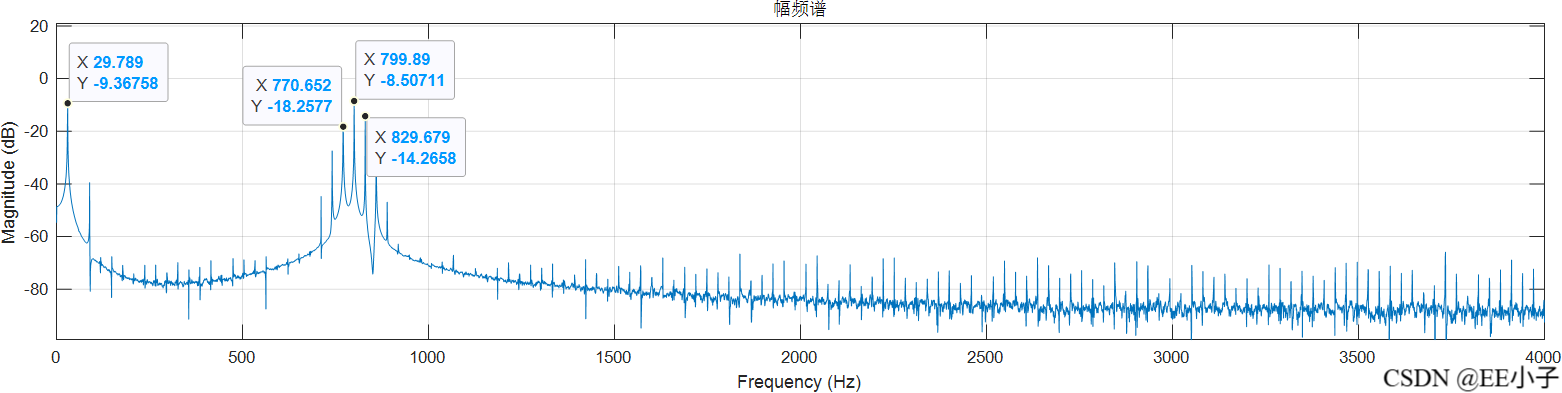
filter_out

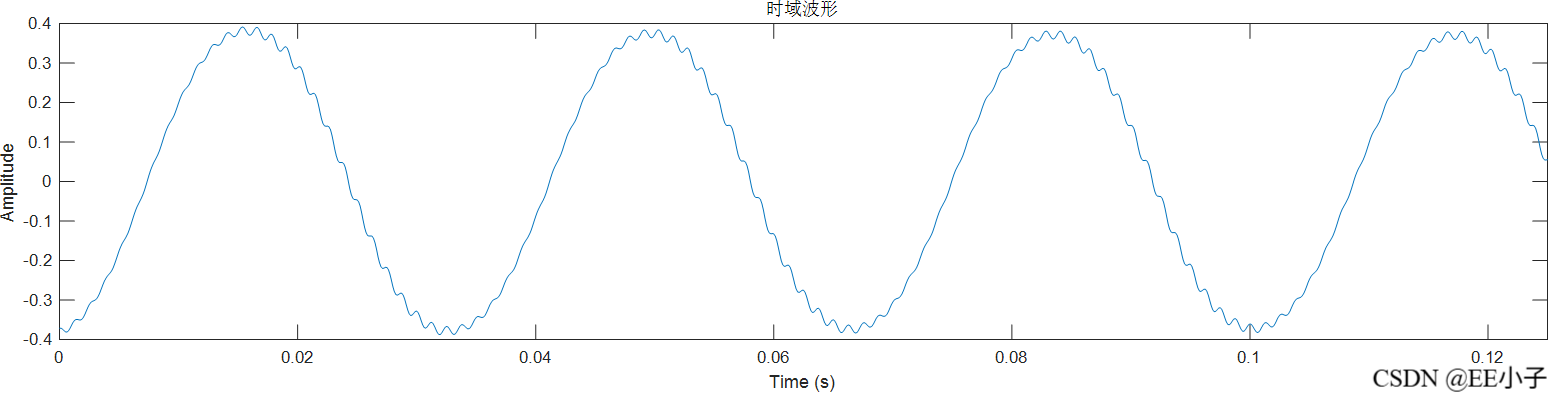
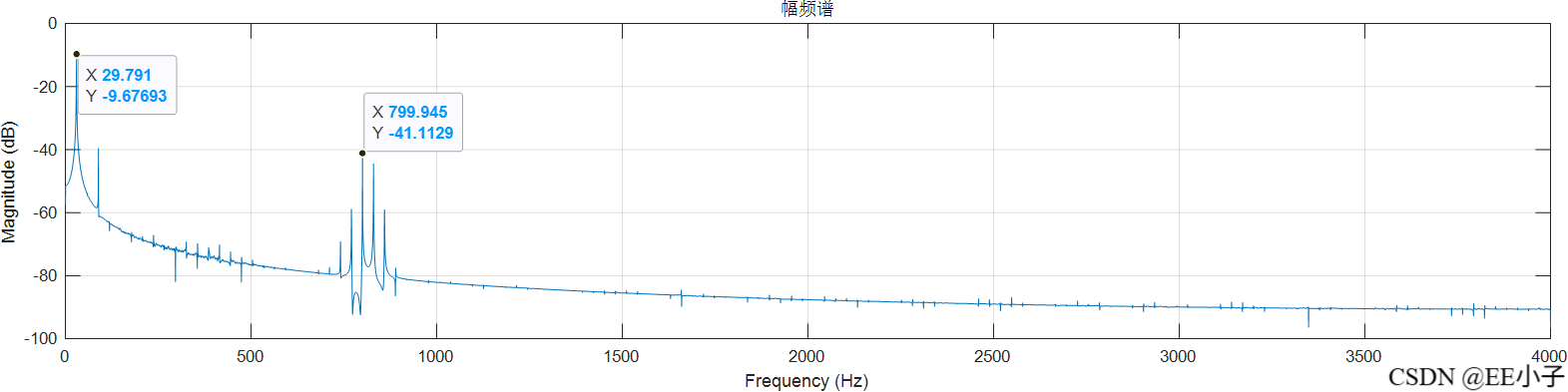
dout

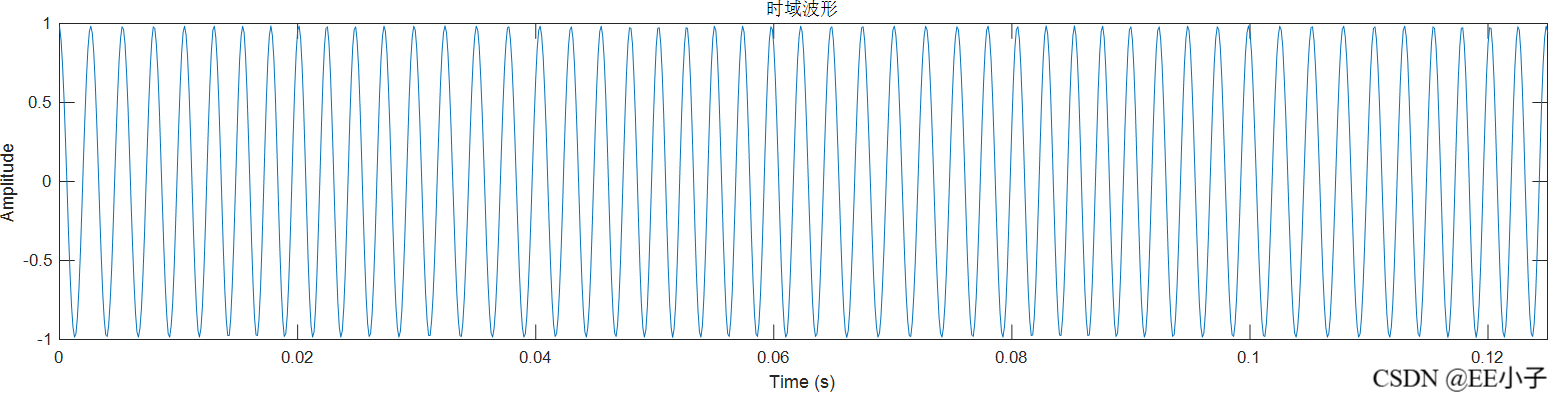
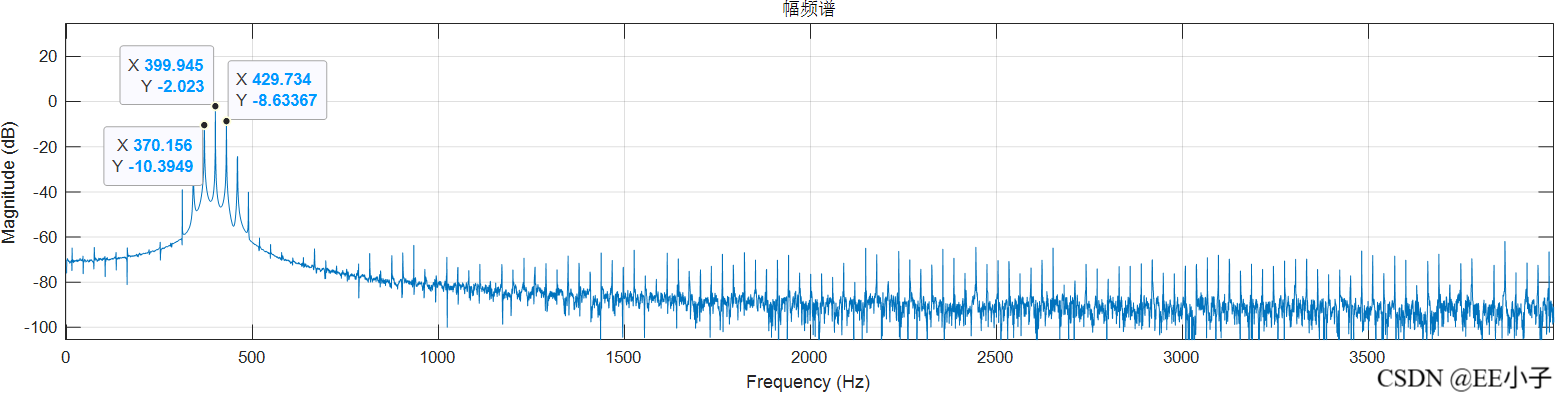
三、数字系统二仿真（Quartus+Modelsim）

300Hz输入信号，其余与数字系统是规格一致。

mult_out

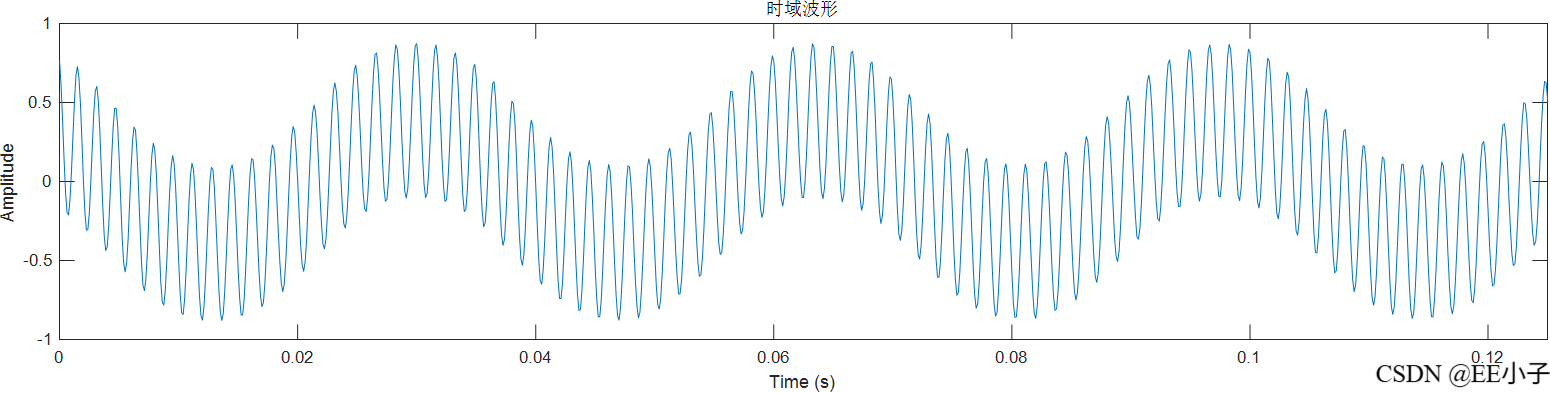
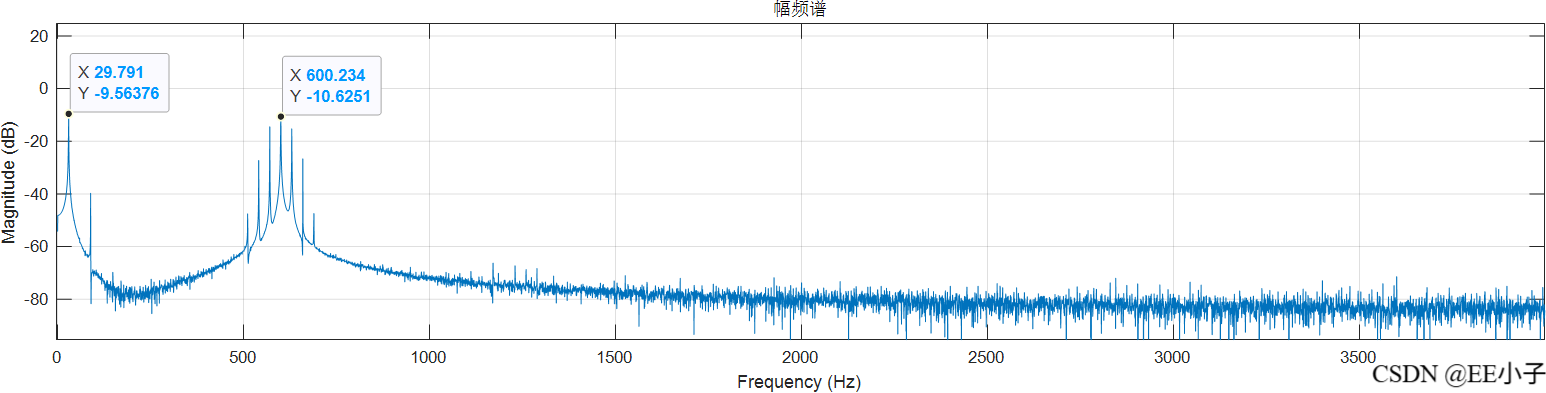
filter_out

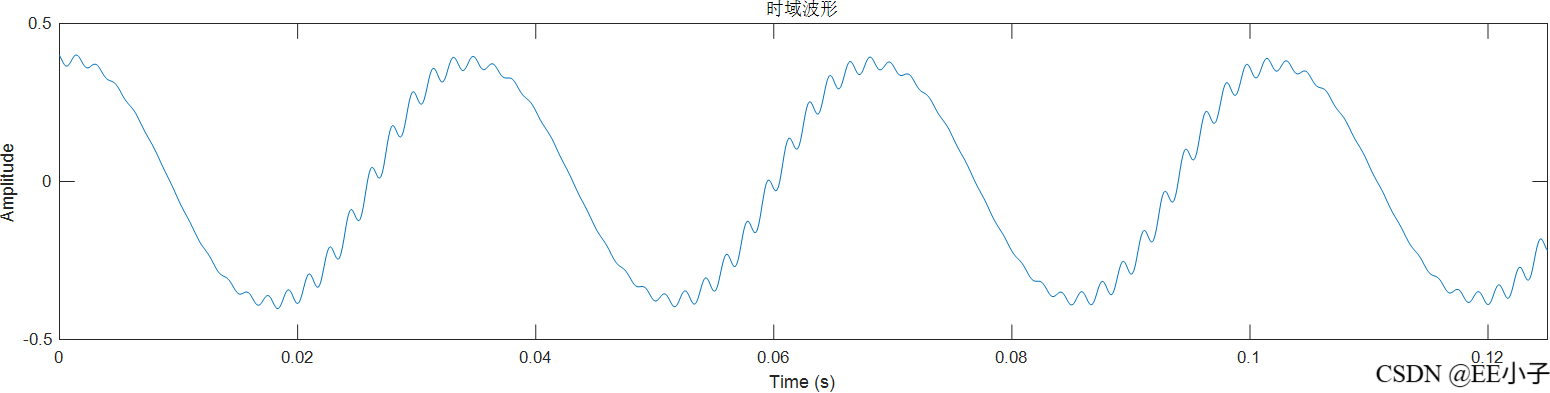
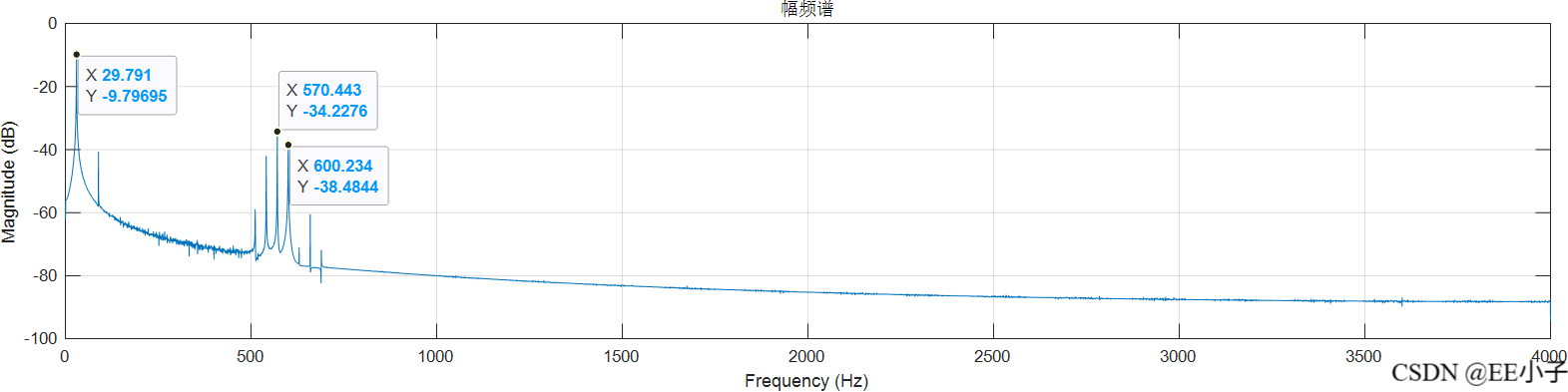
dout

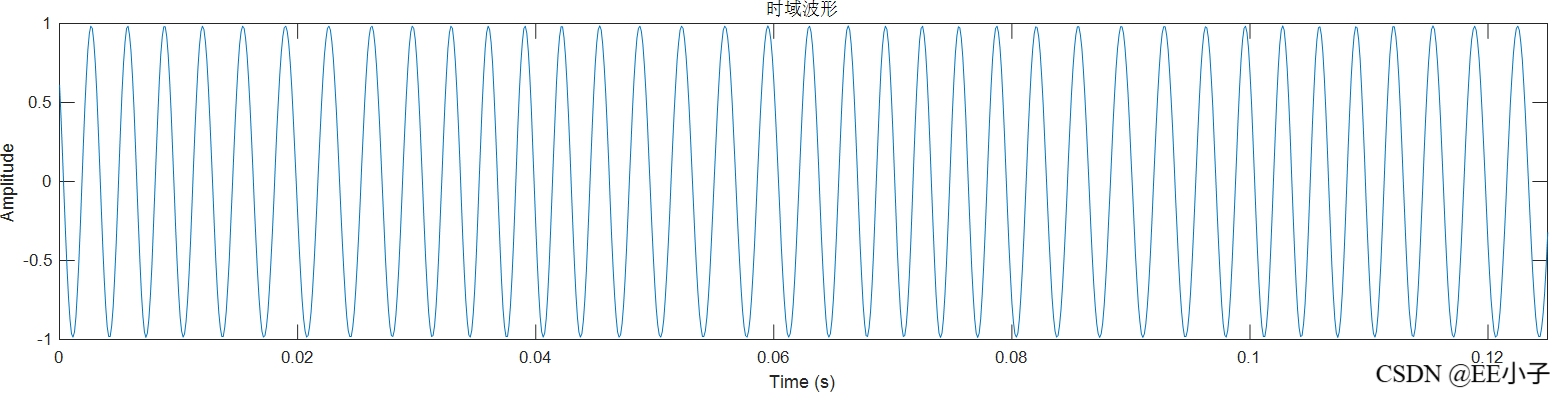
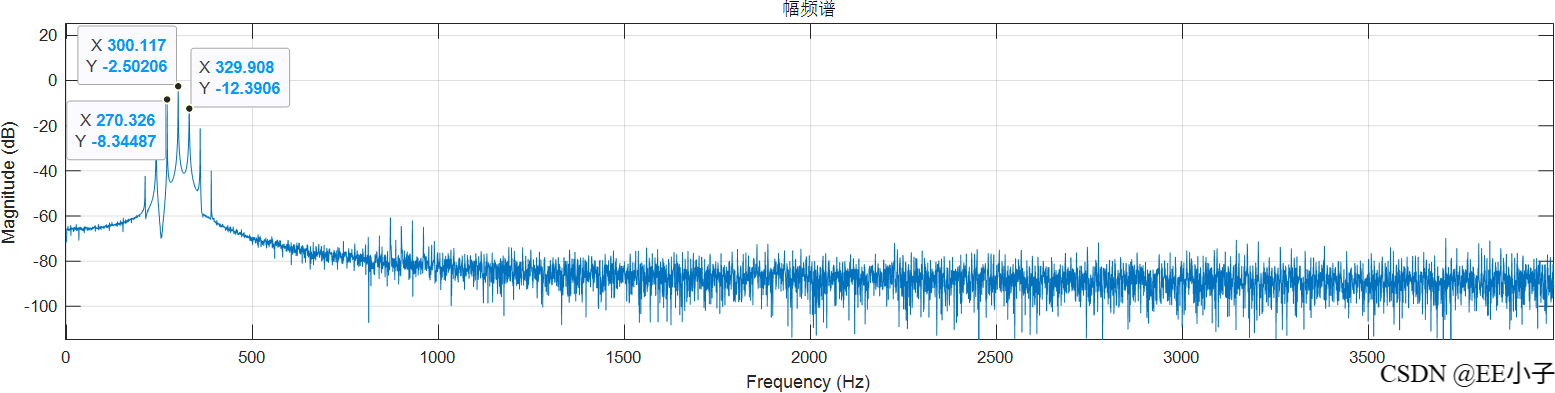
四、数字系统三仿真（Quartus+Modelsim）

NCO Generation Algorithm : small rom,样点数12501,其余与数字系统一规格一致。

mult_out

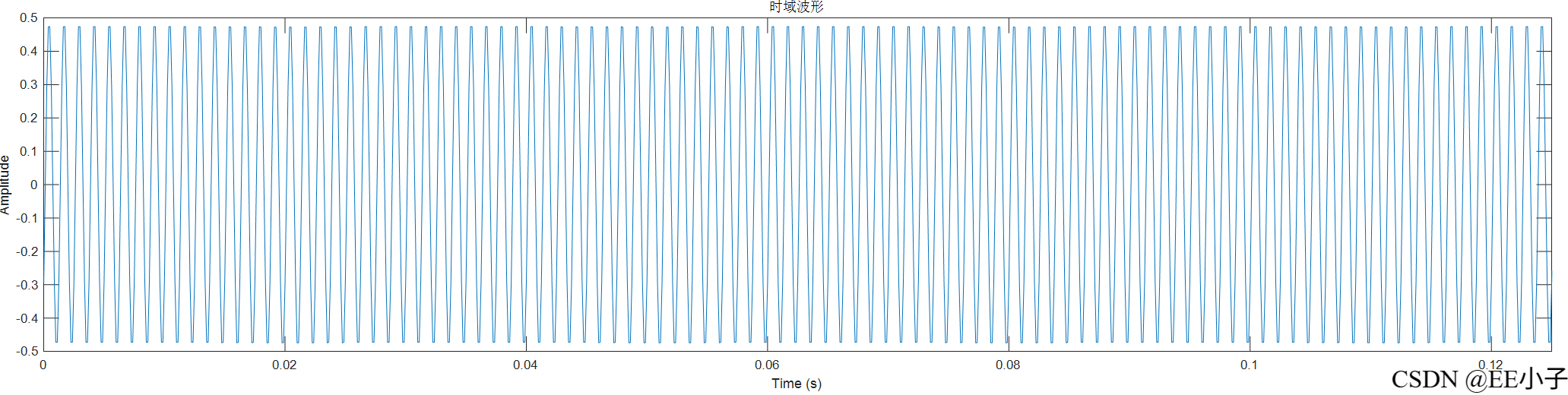
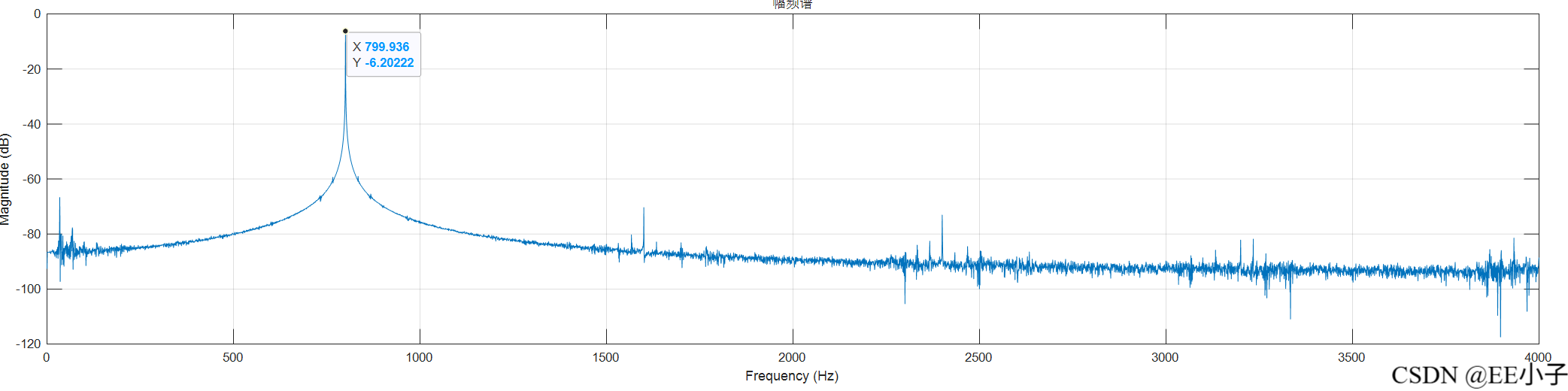
filter_out

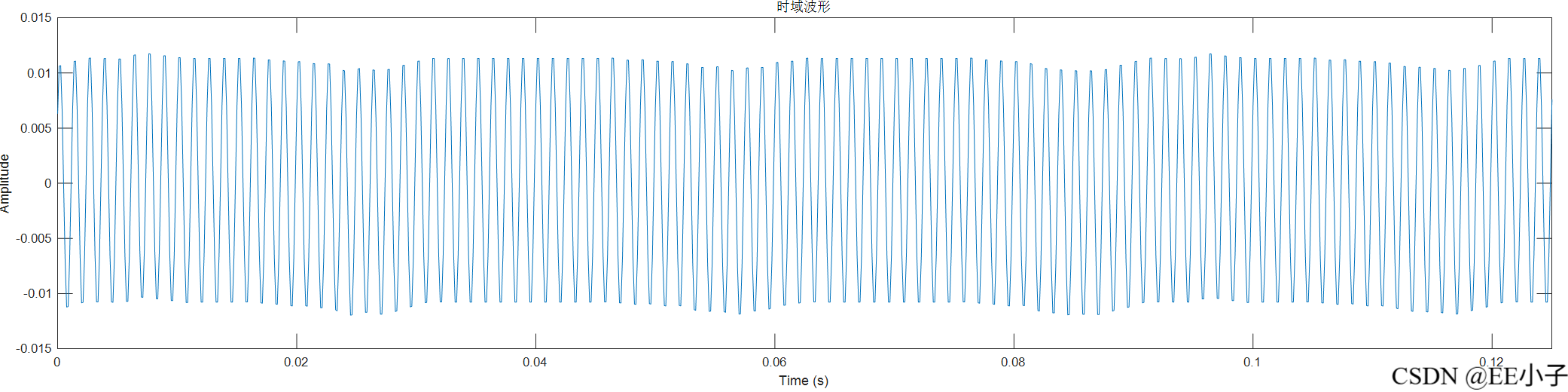
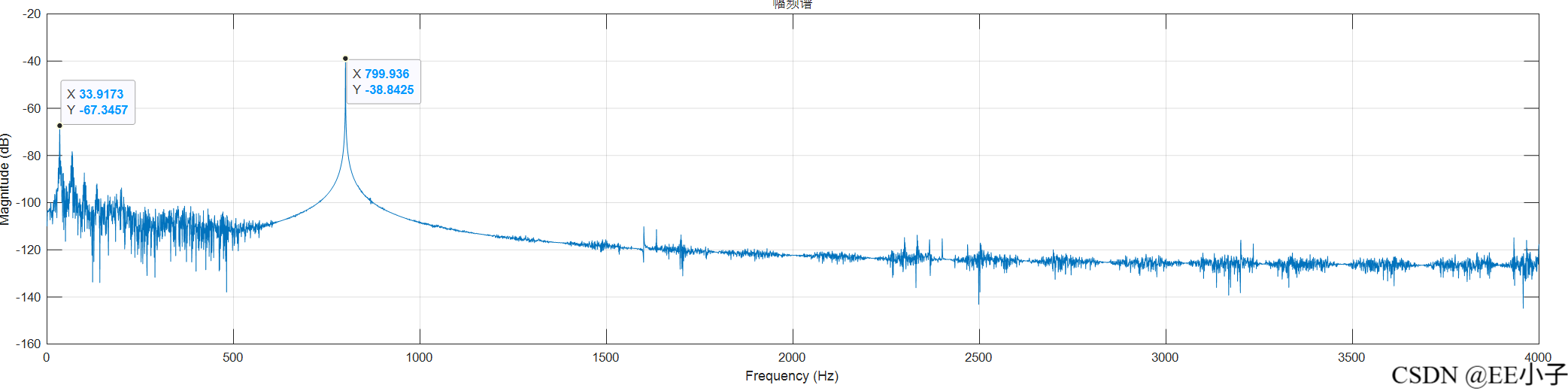
dout

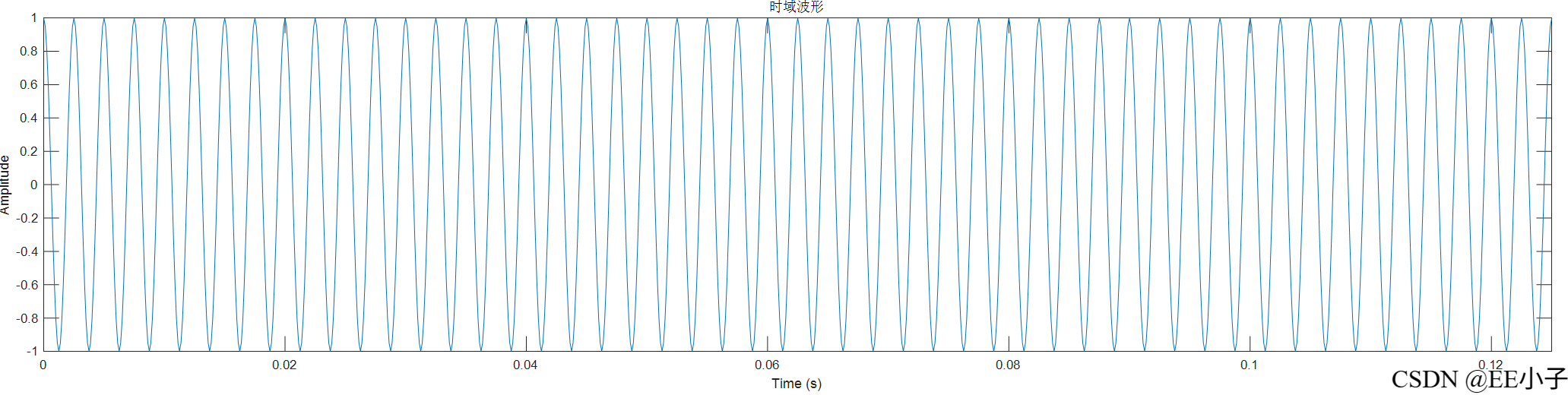
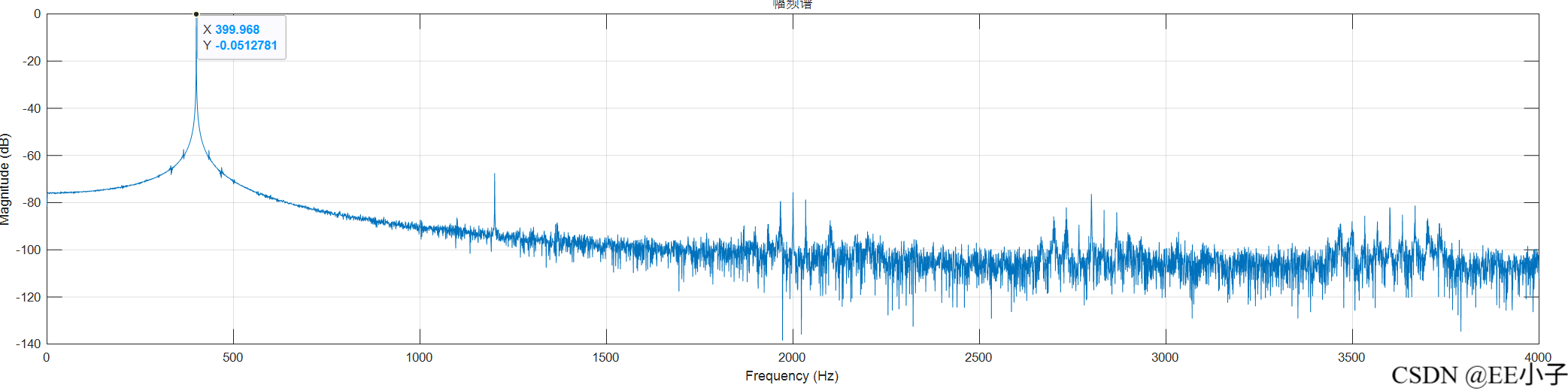
五、现象

可以发现，最开始的模拟系统仿真结果是符合我们的预期的，但是数字系统的仿真结果却出现了类似频率调制的现象。为了确定该现象的原因，又进行了300Hz的仿真实验，发现无影响。所以可以确定该现象是系统造成的。最后对NCO实现架构进行更改，发现结果符合预期。

六、数字PLL系统再分析

为什么会这样呢？先说结论，只是替换了NCO Generation Algorithm，对整个系统的影响只在于数字实现所带来的延时改变了，延时对应影响数字系统的相位响应，不同于幅频特性可以在量化时采用尽可能大的位宽去近似模拟系统的真实量，数字实现必然会带来延时，从而恶化系统相位裕度，要想了解具体细节，我们就要详细分析一下真实的数字系统模型究竟是怎样的。

概念

相位裕度（Phase Margin,PM）

物理含义：开环相移还可以增加，系统才到达临界稳定状态。

增益裕度（Gain Margin,GM）

物理含义：系统的放大能力再增加多少倍（或减少多少 dB），系统才到达临界稳定状态。

 

先来看NCO(离散积分器)建模：

为构造的误差函数，也可以理解为电压控制函数

系统函数

PLL系统分析

建模

其中(为简便公式，忽略微小的舍入误差)，

   ,   ,

,

    ,  ,

，

假设滤波器对和频项抑制情况良好下效果近似为理想低通滤波器

其中Δθ为稳态工作点，Δφn微扰相差。

假定，则时域模型

其中

所以

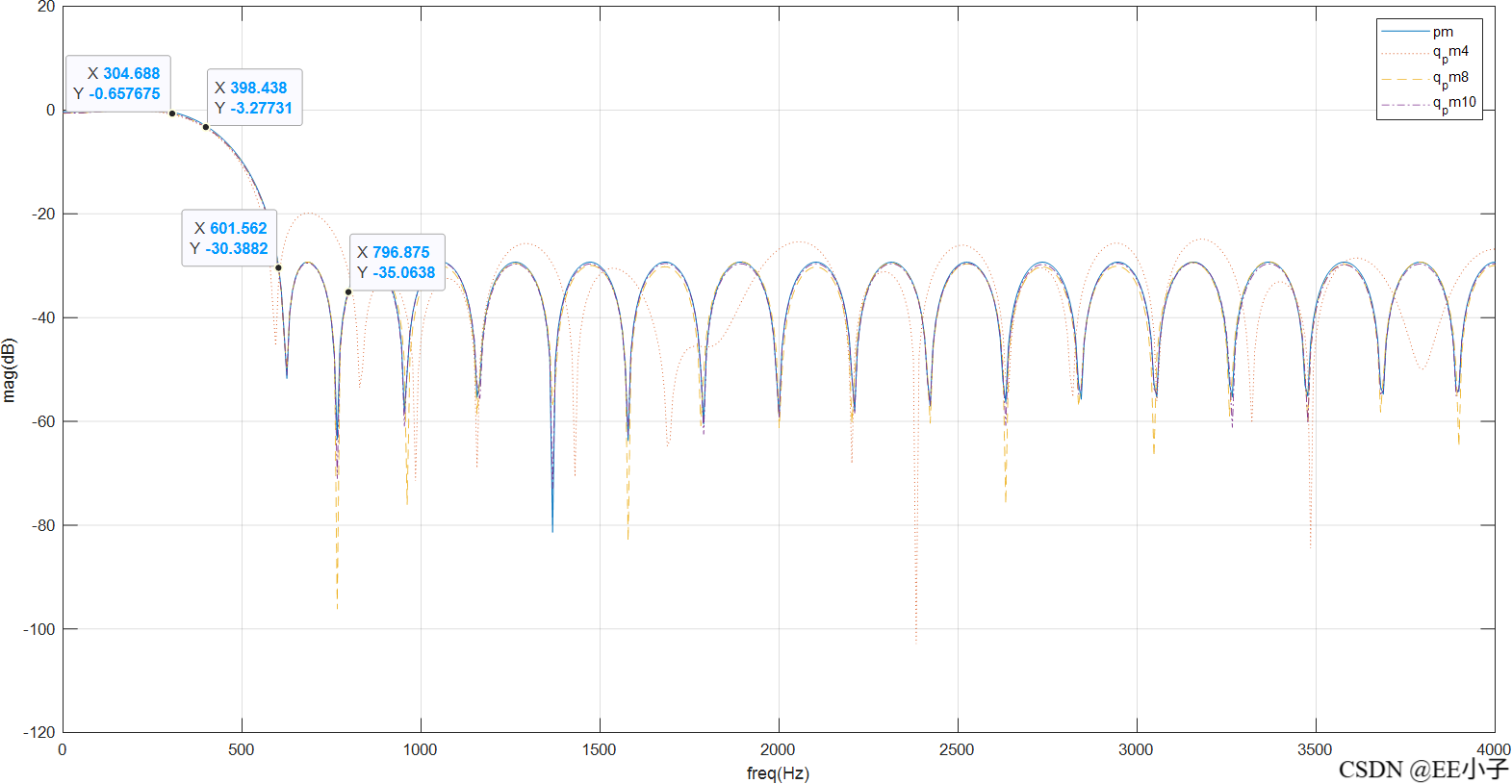
对系统函数进行MATLAB仿真，使用Barkhausen stability criterion和Root Locus Techniques两种方法加强说明。

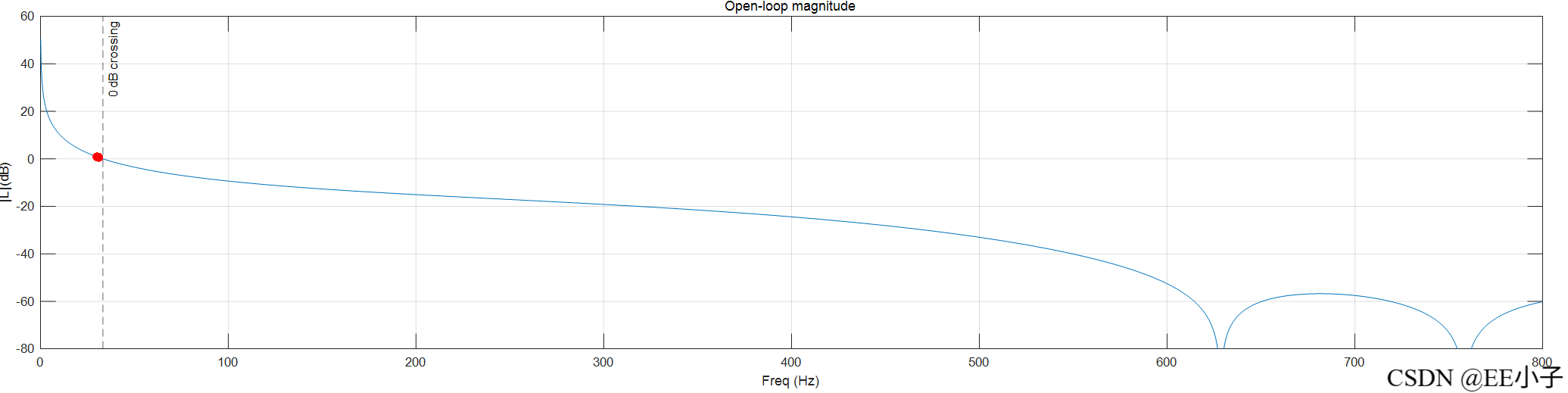
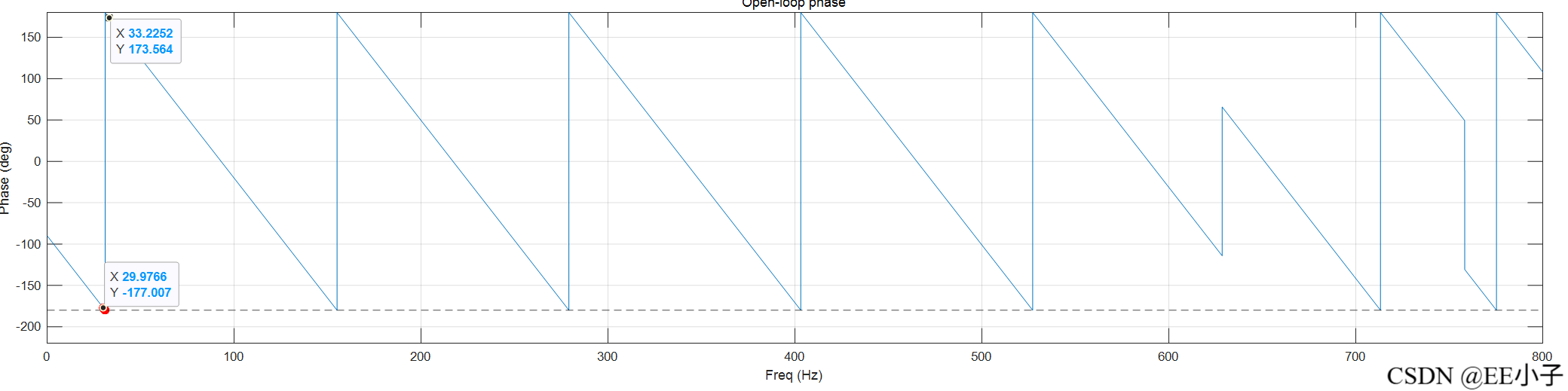
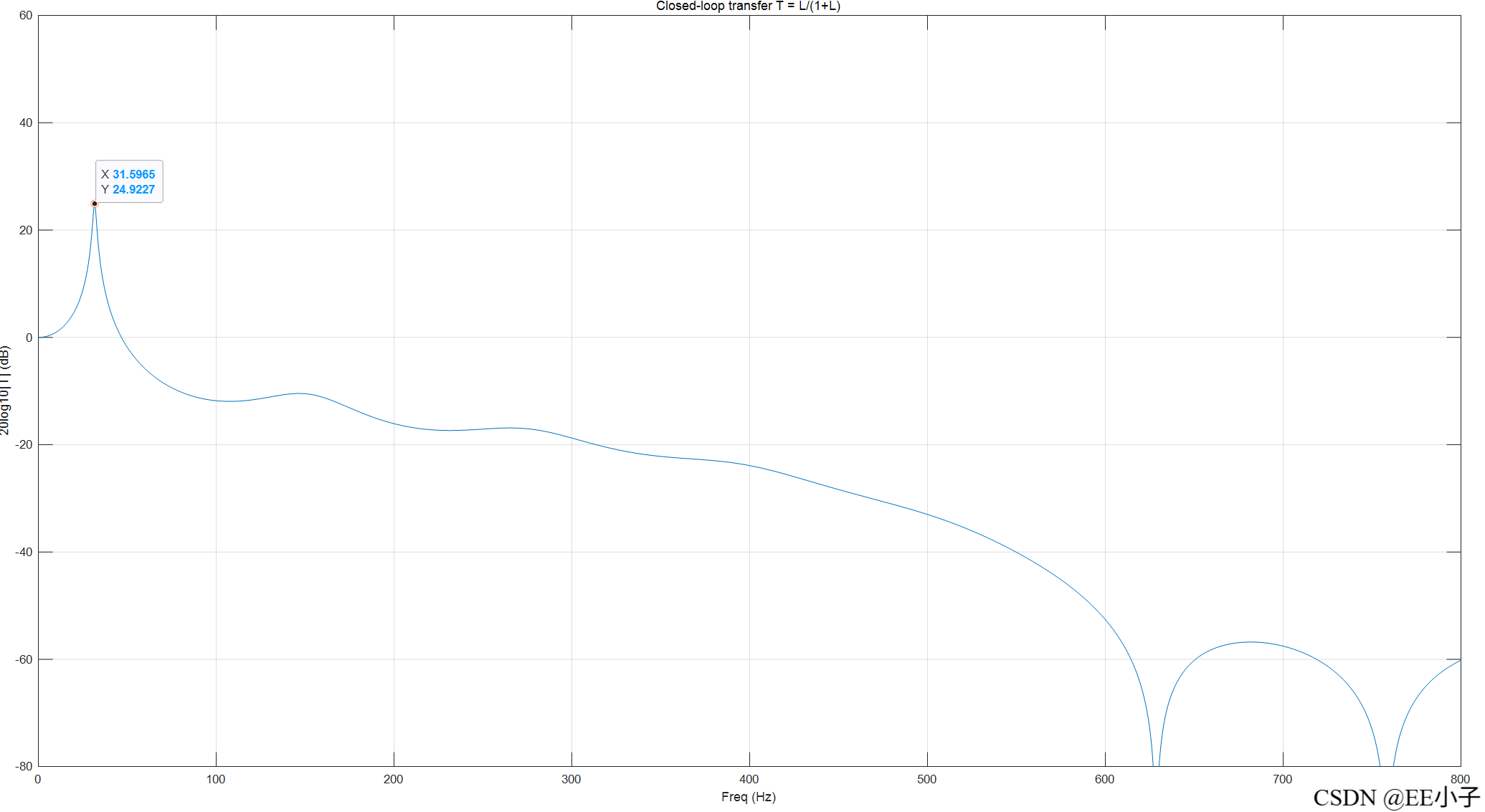
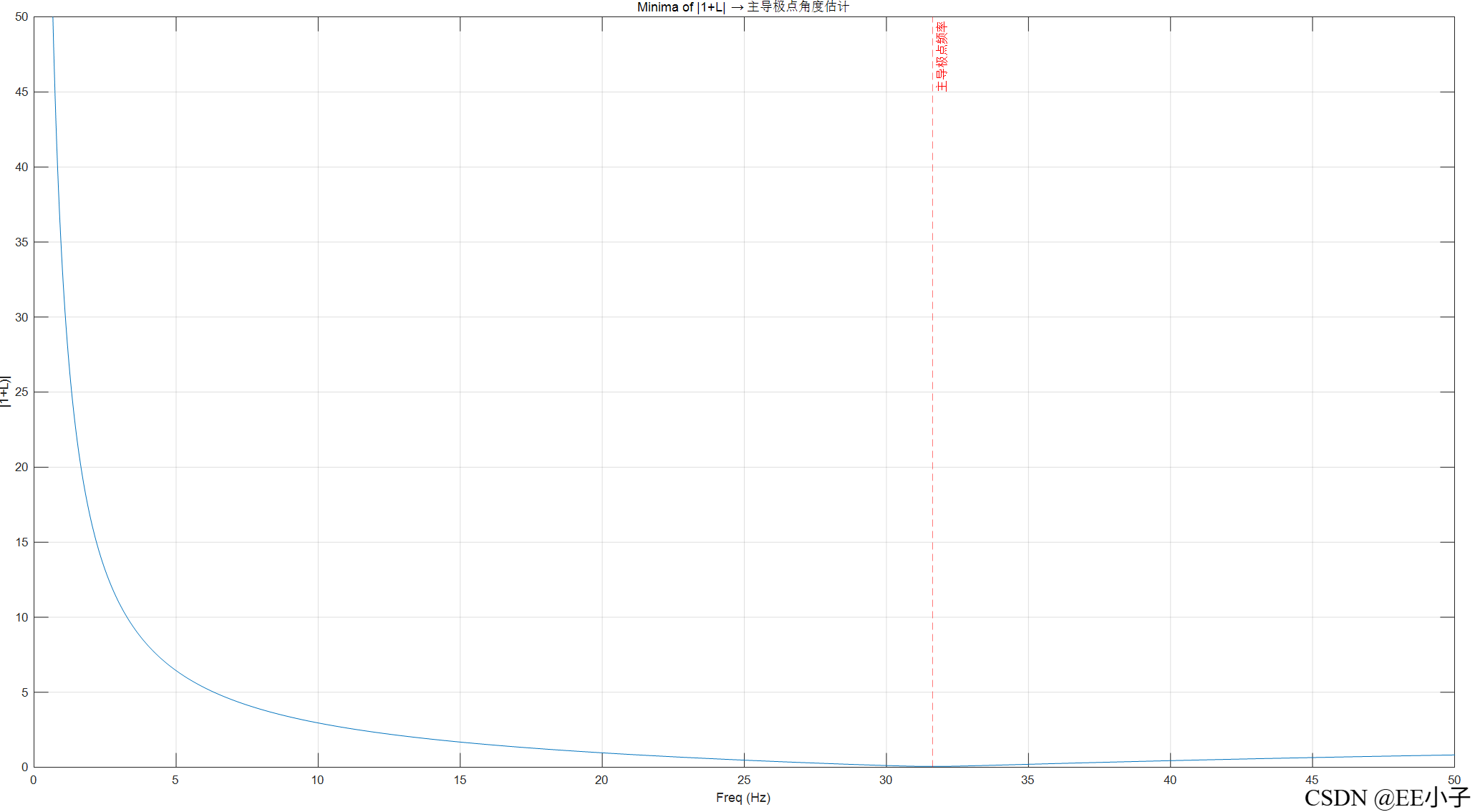
七、解释

从仿真结果来看，该数字系统确实在30Hz附近存在闭环振荡的可能。

线性角度：Barkhausen 条件是“离散的方程”，解通常是点

把系统线性化后，开环幅频响应写成。边界振荡/自激的数学条件是：

⟺ 

这是一个复数方程（两个实条件：相位与模长同时匹配）。解这两个条件通常不会给出“连续区间”的频率，而是若干离散解（或没有解）。

因此，即使相位在一段频率上接近 −180°，幅度精确到 1 的点通常只有一两个 —— 那些点就是“数学上确切的自激候选点”。

非线性： 量化如何“选频”并产生窄线

·  在实际开环 Bode 中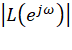，在某段频率上可能大于 1（或接近 1），并且相位在那段也接

近 −180°。这会在闭环传递函数 =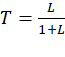上造成一个尖峰（resonant peak），即在那段频带信号会被放大 — 这是“带状放大”的来源。

·  但尖峰有有限带宽（由增益相对变化和相位斜率决定）。如果这个尖峰很陡峭（Q 高），它在频率上是很窄的。闭环系统对噪声/扰动的频谱会把能量集中在这个峰附近。