二探锁相环：二阶系统概论

一、前言

二阶低通的标准形式是

其中​ 是自然频率， 是阻尼比。

这里就出现了“麻烦”：

• 当 ζ≈0.707（所谓 Butterworth 响应），幅频特性在 ω=ωn 处正好下降 3 dB，我们可以直接说 ωc=ωn。
• 当 ζ比 0.707 大（阻尼强），曲线更“平缓”，3 dB 点会在 ω<ωn ​。
• 当 ζ比 0.707 小（阻尼弱），曲线有共振峰，3 dB 点甚至会“绕”到峰值之后去。

也就是说，二阶系统的截止频率不再等于自然频率，而是由阻尼决定的。

二、以rc低通滤波器为环路滤波器

环路滤波器

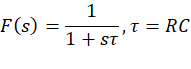
系统

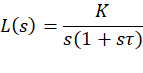
由闭环特征方程

得到标准二阶特征多项式

所以

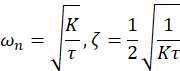
环路滤波器-3dB截止频率

求解系统-3dB截止频率

补充误差传递函数

幅度平方函数为

令, 在 −3 dB 点，幅度平方等于 1/2。代入并化简得到关于 r 的方程：

令,得到二次方程

其正根为

所以-3dB频率为

三、以无源比例积分滤波器为环路滤波器

环路滤波器

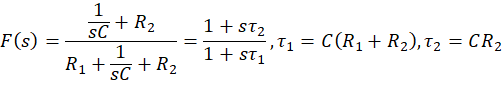
系统

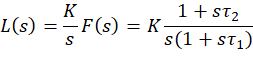
由闭环特征方程

得到标准二阶特征多项式

所以

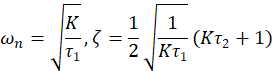
环路滤波器-3dB截止频率

幅度平方函数为

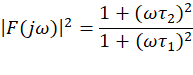
所以-3dB频率为

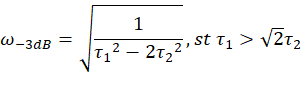
即

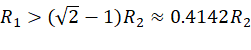
结论

若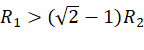，则该滤波器的幅频会在某处下降至 −3 dB（相对于直流 0 dB），解为上面的。

若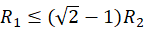，则方程没有实解：意味着幅度谱不会下降到 −3 dB（相对于 DC）；换句话说，滤波器的幅频在整个频率轴上都保持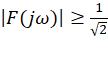。物理直觉：这个滤波器在低频是 1（0 dB），经极点产生衰减后，又被高频零点部分抵消回升——是否真正“凹”到 −3 dB，取决于极点与零点间的间隔（也就是 R1 与 R2 的比值）。

求解系统-3dB截止频率

补充误差传递函数

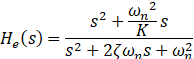
则幅度平方函数为

令, 在 −3 dB 点，幅度平方等于 1/2。代入并化简得到关于 r 的方程：

令,得到二次方程

其正根为

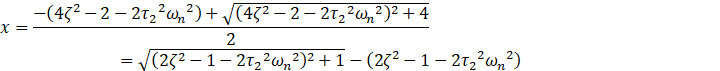
所以-3dB频率为

四、以有源比例积分滤波器为环路滤波器

环路滤波器

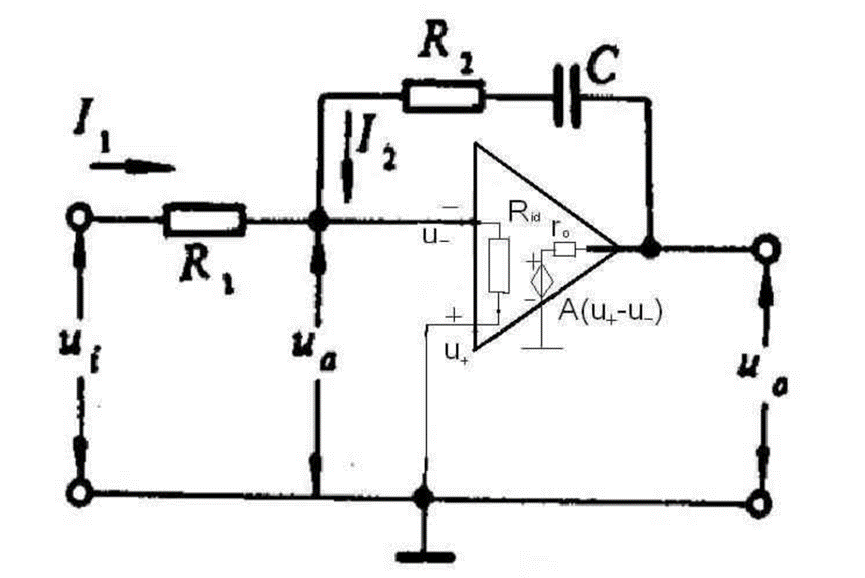
推导

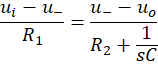
易得

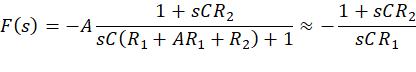
若定义相位误差与上两例相反，则得到相同形式的系统闭环函数表达式，也就是说的符号不影响得到的物理结论。

令,这里直接得到

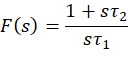
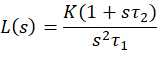
由闭环特征方程

得到标准二阶特征多项式

所以

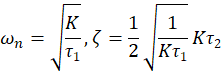
环路滤波器-3dB截止频率

幅度平方函数为

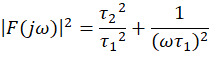
所以-3dB频率为

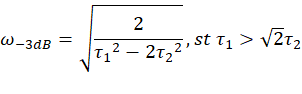
求解系统-3dB截止频率

补充误差传递函数

幅度平方函数为

令, 在 −3 dB 点，幅度平方等于 1/2。代入并化简得到关于 r 的方程：

令,得到二次方程

其正根为

所以-3dB频率为