一、仿真实验
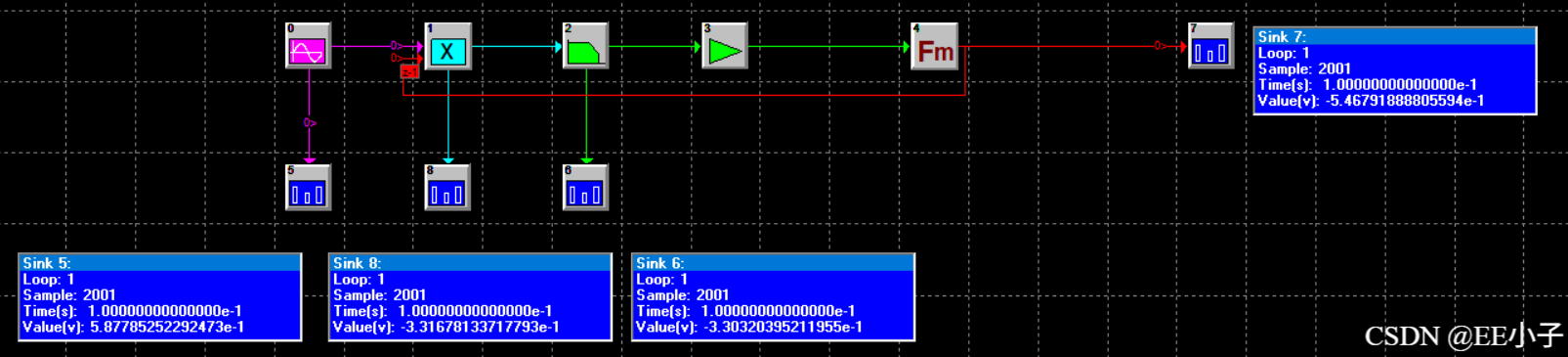
仿真系统参数表
|
编号 |
属性 |
参数 |
|
Token0 |
Source |
Amp = 1 v; Freq = 64 Hz; Phase = 0 deg; Output 0 = Sine t5 t1; Output 1 = Cosine; Max Rate (Port 0) = 20e+3 Hz |
|
Token1 |
Multiplier |
Inputs from t0p0 t4p0; Outputs to 2 8; Max Rate = 20e+3 Hz |
|
Token2 |
Operator |
Chebyshev Lowpass IIR; 4 Poles; Fc = 150 Hz; Quant Bits = None; Init Cndtn = Transient; DSP Mode Disabled; Max Rate = 20e+3 Hz |
|
Token 3 |
Operator |
Gain = 1; Gain Units = Linear; Max Rate = 20e+3 Hz |
|
Token 4 |
Function |
Amp = 1 v; Freq = 100 Hz; Phase = 0 deg; Mod Gain = 100 Hz/v; Output 0 = Quadrature (Sin) t1 t7; Output 1 = In-Phase (Cos); Max Rate (Port 0) = 20e+3 Hz |
|
Token5/6/7/8 |
Sink |
—— |
二、理论分析
因为
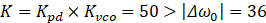
所以静态上可以锁定。
稳态相差
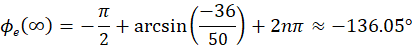
三、仿真结果
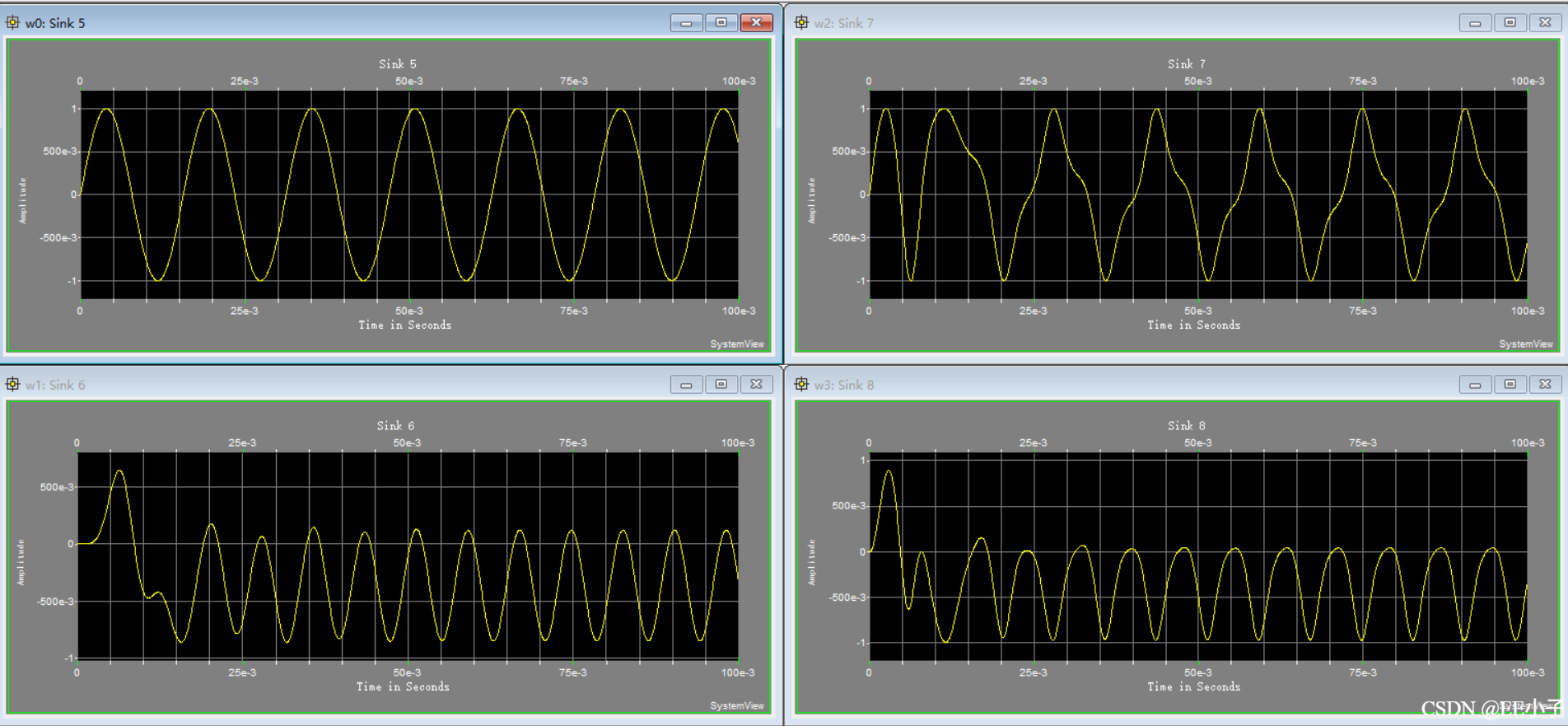
仿真时长0.1s,仿真结果显示,输出信号畸变。
延长仿真时间至1.5s,将后1s仿真数据导入Matlab分析。
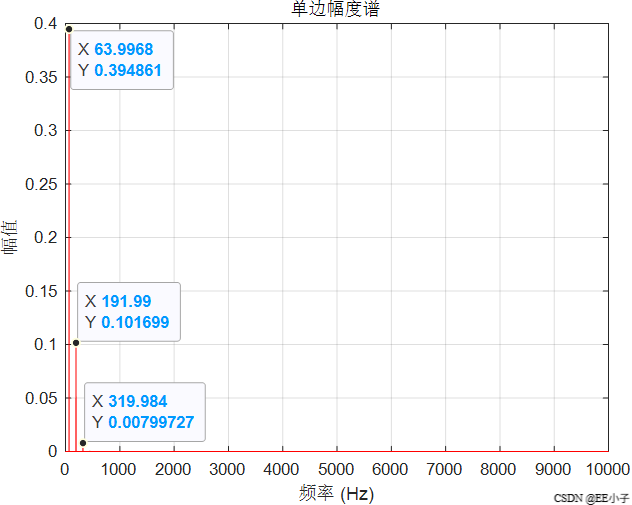
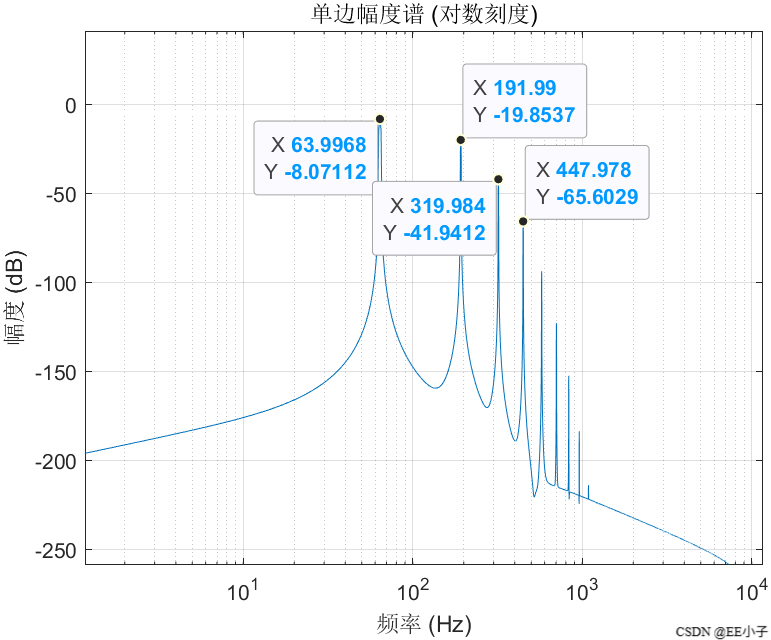
四、再分析
根据仿真结果重新进行理论分析
乘法鉴相器在锁定时会在控制电压里产生一个强烈的「和频」纹波。
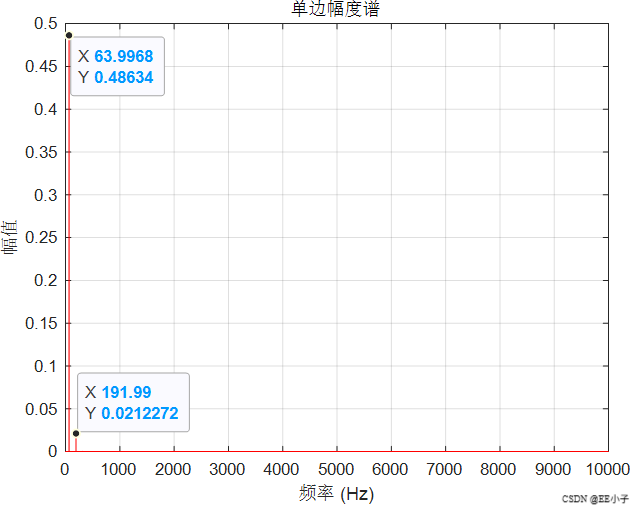
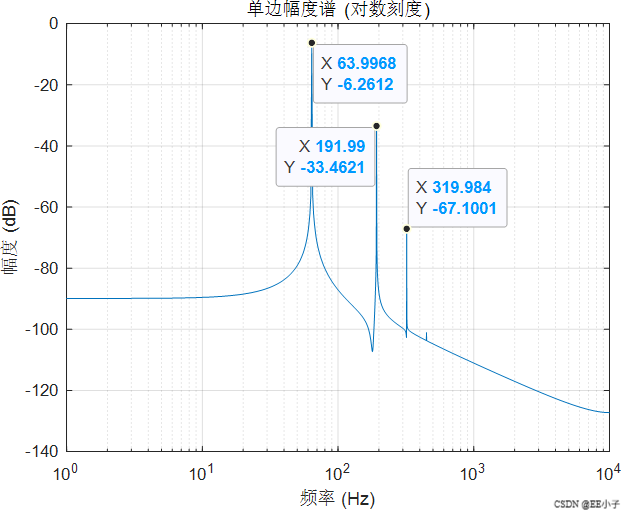
当参考与 VCO 都是 64 Hz 时,乘法器输出包含DC和128 Hz两项。低通 fc=150 Hz 把 128 Hz 基本放了进去,这就让 VCO 的控制电压带着 128 Hz 的频率调制。相位以 128 Hz 在 64 Hz 正弦上“抖”,经 Bessel 展开后,输出就会在 fc±n⋅128 Hz周围出现边带。因为载频本身就是 64 Hz,64±128=64,192(三倍频),更高阶会到 320(五倍频)……于是在 MATLAB 里看到的频谱正好是 64、3×64、5×64,而且幅度随阶数迅速衰减(0.79/0.20/0.01 的比例也符合“频率调制小指数 β 时,J₁、J₃、J₅ 迅速变小”的现象)。
设输入参考信号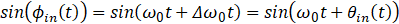
VCO输出信号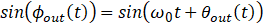
正弦鉴相器输出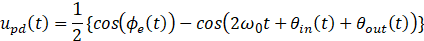
仿真结果显示,锁定后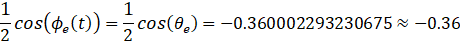
所以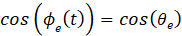 是直流/低频相位误差信号;
是直流/低频相位误差信号;
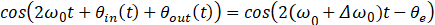 是两倍频(128 Hz)拍频项。
是两倍频(128 Hz)拍频项。
低通 fc=150 Hz 几乎把 128 Hz 放了进去(此时滤波器增益约为0.3dB),于是 VCO 控制电压里不但有 DC,还带着128 Hz 的余波。
所以VCO的输出相位
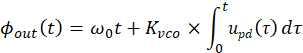
得
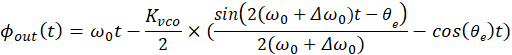
因此 VCO 输出等价于以 2ω(=128 Hz)为调制频率、调制指数 β的“频率调制”:
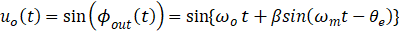
其中
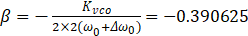
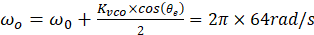
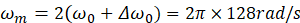
由Jacobi–Anger 展开
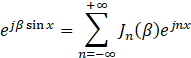
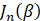 是第一类贝塞尔函数。它把“指数里含有正弦的指数”展开成“许多谐波指数的线性组合”。
是第一类贝塞尔函数。它把“指数里含有正弦的指数”展开成“许多谐波指数的线性组合”。
所以
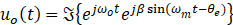
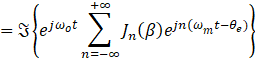
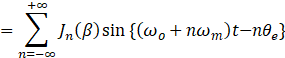
也就是说,在载频
(64 Hz)两侧,每隔
(128 Hz)一条边带,幅度系 Bessel 函数
同时,小调制指数时,Bessel 近似
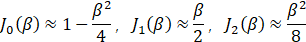
由于上面的“频率重合”,
- 64 Hz 处的幅度近似由
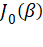 与
与 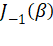 (来自 -64 Hz)等项矢量叠加,数值近似为
(来自 -64 Hz)等项矢量叠加,数值近似为 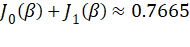
- 192 Hz 处主要由
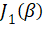 与
与 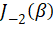 叠加,数值近似为
叠加,数值近似为 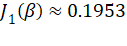
- 320 Hz 数值近似为
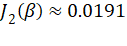
在误差允许范围内,理论分析数值结果与仿真结果近似。从而验证了“128 Hz 相位抖动 → Bessel 边带”的机理。
尝试收窄滤波器带宽(fc=80 Hz)后,输出信号调频失真畸变大幅减轻,进一步说明理论分析的准确性。




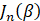
















 6153
6153

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








