通信系统（1）：调制解调原理FM&PM

一、符号定义

载波的一般形式

其中与瞬时角频率、瞬时频率

二、相位调制（PM）

把信息直接叠加到相位上

其中是调制信号，是相位灵敏度

对于正弦调制的具体关系

定义相位指数

输出

三、频率调制（FM）

把信息叠加到瞬时频率上

等价的，相位是频率的积分

因此 FM 与 PM 在数学上是相互关联的：FM 可以看成对输入做一次积分后作为 PM；反之 PM 可视作 FM 对信号导数的形式（在某些变换下等价）。

对于正弦调制的具体关系

定义相位指数

输出

四、总结

注意差异

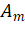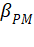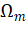• 对于同一幅度 ,PM的调制指数 ​与调制频率 无关；

  FM 的调制指数 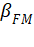与调制频率 成反比（​）。
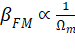  → 这意味着：在相同调制幅度下，低频调制（小 Ω）会产生更大的 FM 指数，因此更丰富更强的边带。

频谱与调制指数

当相位是正弦的（PM 或 FM 都能写成如下形式），输出可以用贝塞尔函数展成无穷侧带：

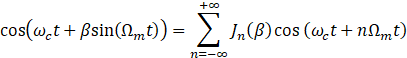
关键结论：

• 不管 FM 还是 PM（当相位项包含正弦时），都会产生无限多个侧带，幅值由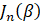（贝塞尔函数）给出；
• 当 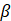很小（小角近似），只有载波和第一阶侧带重要，侧带幅度与  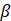成正比（线性近似）；

Carson 规则（经验）

FM 的总带宽大致

其中是峰值频偏，