FPGA/Quartus学习日志（3）：NCO_IP_CORE

一、Parameters

1、Phase Accumulator Precision(相位累加器精度)

相位累加器（Phase Accumulator）

• 每个时钟周期累加一个 相位增量值（FCW, Frequency Control Word）。
• 累加结果就是当前的相位值。

2、Angular Resolution（角度分辨率）

定义

• 指相位累加器输出到波形查找表（LUT）时，用于查表的 相位位数。
• 控制相位到波形索引的精细程度。

原理

• 相位累加器的位宽可能很大（比如 32 位），但波形表不可能有 2^32 个采样点，那会占用巨量 ROM。
• 所以 NCO 只取相位累加器的 高几位 作为 ROM 地址，这个高几位的数量就是 Angular Resolution。

影响

• Angular Resolution 高 → ROM 地址多 → 波形更平滑 → 杂散小（SFDR 高）
• Angular Resolution 低 → ROM 地址少 → 波形台阶感明显 → 杂散大，但资源占用少

举例

• 相位累加器：32 位
• Angular Resolution：10 位
• 波形表深度： 2^10 = 1024 个采样点
• 每个采样点代表 360°/1024≈0.3516°的相位间隔

3、Magnitude Precision（幅度精度）

定义

• 指波形表（ROM）每个采样点存储的幅度数据的位数。
• 也就是 正弦/余弦值的量化精度。

影响

• Magnitude Precision 高 → 幅度刻度细 → 失真小，信噪比高 → 占用存储多
• Magnitude Precision 低 → 占用存储少，但幅度量化误差大，输出波形失真大

举例

• Magnitude Precision = 12 → 每个采样点用 12 位存储幅度值（0~4095）
• 如果输出到一个 12 位 DAC，就非常匹配
• 如果输出只接到一个 8 位 DAC，那 12 位精度就有点浪费

4、总结

• Phase Accumulator Precision（相位累加器精度）

NCO 里相位累加器寄存器的位宽（比如 32 位），决定了频率分辨率（Freq Resolution = f_clk/2^(PhaseAccWidth)）。

• Angular Resolution（角度分辨率）

从相位累加器的高位中取多少位做查表地址。决定 LUT 的深度。

• Magnitude Precision（幅度精度）

LUT 每个采样点存储的幅度值位宽（比如 12 位、16 位），决定输出幅度的量化精度。

Angular Resolution和 Magnitude Precision二者独立设置

二、思维误区

错误想法：

若Angular Resolution = 10 ，则LUT只有1024 个采样点，如果使用10位宽Magnitude Precision，则刚好覆盖0000000000--1111111111，而位宽小于10，则不能填满1024个地址，位宽大于10则会有一些值超过地址覆盖范围。

但实际上 NCO 的 LUT 是二维的概念：

• 横向（地址）由 Angular Resolution 决定
• 纵向（存储值）由 Magnitude Precision 决定

它们在硬件结构上是两组完全独立的位宽参数：

• LUT 的地址宽度由 Angular Resolution 决定
• LUT 的数据宽度由 Magnitude Precision 决定

所以 Magnitude Precision 和 Angular Resolution 在数值上没有必然的大小关系，只是在最终输出质量上会共同作用。

假设：

• Phase Accumulator Precision = 32
• Angular Resolution = 10（即 1024 点的波形表）
• Magnitude Precision = 14（幅度值用 14 位表示）

硬件含义：

• 相位累加器每个时钟加一个增量（频率控制字），精度 2^{-32}
• 取累加器高 10 位作为 LUT 地址（共 1024 个采样点）
• 每个 LUT 采样点存 14 位幅度值（即纵向有 2^14 个离散刻度）

这样虽然“横向采样点”只有 1024 个，但每个点的“纵向幅度刻度”很细（14 位），输出到 DAC 时纵向失真会小。

举例说明

例子设定

• 相位点数（Angular Resolution）固定为 8 个点（地址 0~7，对应 0°, 45°, 90°, ...）。
• 正弦波：

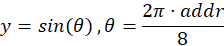
• 量化规则（有符号）：

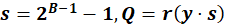
• B = 4 → S=7
• B = 6 → S=31

真正用 4 位 生成 LUT

地址	θ (°)	真值 y	S=7	LUT整数 Q	重构值 Q/S	误差
0	0	0.000000	7	0	0.000000	0
1	45	0.707107	7	5	0.714286	+0.007179
2	90	1.000000	7	7	1.000000	0
3	135	0.707107	7	5	0.714286	+0.007179
4	180	0.000000	7	0	0.000000	0
5	225	-0.707107	7	-5	-0.714286	-0.007179
6	270	-1.000000	7	-7	-1.000000	0
7	315	-0.707107	7	-5	-0.714286	-0.007179

真正用 6位 生成 LUT

地址	θ (°)	真值 y	S=31	LUT整数 Q	重构值 Q/S	误差
0	0	0.000000	31	0	0.000000	0
1	45	0.707107	31	22	0.709677	+0.002570
2	90	1.000000	31	31	1.000000	0
3	135	0.707107	31	22	0.709677	+0.002570
4	180	0.000000	31	0	0.000000	0
5	225	-0.707107	31	-22	-0.709677	-0.002570
6	270	-1.000000	31	-31	-1.000000	0
7	315	-0.707107	31	-22	-0.709677	-0.002570

把 4 位整数左移 2 位当作 6 位（4 位 Q × 4，相当于左移 2 位，范围虽然变成了 ±28，但值不是重新计算出来的）

地址	θ (°)	原4位整数 Q	左移2位 Q'	重构值 Q'/31	真值 y	误差
0	0	0	0	0.000000	0.000000	0
1	45	5	20	0.645161	0.707107	-0.061946
2	90	7	28	0.903226	1.000000	-0.096774
3	135	5	20	0.645161	0.707107	-0.061946
4	180	0	0	0.000000	0.000000	0
5	225	-5	-20	-0.645161	-0.707107	+0.061946
6	270	-7	-28	-0.903226	-1.000000	+0.096774
7	315	-5	-20	-0.645161	-0.707107	+0.061946

结果对比

方法	45° 误差	90° 误差
4 位重新量化	+0.007179	0
6 位重新量化	+0.002570	0
4 位直接左移成 6 位	-0.061946	-0.096774

• 真正的 6 位量化：比 4 位误差更小，精度提升明显（量化步长从 1/7 ≈ 0.142857 降到 1/31 ≈ 0.032258）。
• 直接放大：反而比原来更不准，因为数值间的细节根本没增加，只是拉伸了原来的误差。

结论

Magnitude Precision 提高时，必须在 LUT 生成阶段用高精度重新计算，才能真的减少量化误差。

Angular Resolution（相位精度）和 Magnitude Precision（幅度精度）是独立的：

• Angular Resolution 不变时，增加 Magnitude Precision 可以让采样点的纵向精度更高。
• 反之，只是放大低精度数据是徒劳的。

三、Implementation

1、Modulation

(1)Frequency Modulation (频率调制)

• 给 相位累加器 的增量输入（Phase Increment），也就是说它控制每个时钟周期相位累加器增加的值。

•  改变这个输入，相当于动态调整输出波形的频率。

• 简单来说，频率调制输入决定了输出信号的瞬时频率。

• 典型应用：调频 (FM)、扫频（频率扫描）、动态改变输出频率。

• 输入值越大，输出频率越高。

(2)Phase Modulation (相位调制) 输入

• 直接加在相位累加器当前值上的一个相位偏移量。

•  也就是说它直接改变当前的相位值，产生相位偏移。

•  改变这个输入，会导致输出波形在时间上的偏移，但频率保持不变。

• 典型应用：相位调制（PM）、相位调整、相位跳变或相位调节。

• 输入值越大，相位偏移越大，波形相应地提前或滞后。

(3)对比

特征	频率调制 (Frequency Modulation)	相位调制 (Phase Modulation)
作用对象	相位累加器的 增量	相位累加器的 当前相位值
控制输出	改变输出的频率	改变输出的相位
时域表现	输出波形频率变化，周期改变	输出波形时间偏移，相位偏移
应用场景	频率调制 (FM)、扫频	相位调制 (PM)、相位跳变、相位校准
输入端口性质	通常为频率步进值，动态变化	通常为相位偏移量，可以是瞬时的或逐步变化

(4)举例说明

假设条件

·  NCO时钟频率固定为 1 MHz（时钟周期 1μs）

·  相位累加器宽度 16 位（范围 0 ~ 65535）

·  输出波形是正弦波，周期由相位累加器增量（频率控制字）决定

频率调制 (Frequency Modulation) 示例

频率控制字 (Phase Increment) = 6553
输出频率计算：

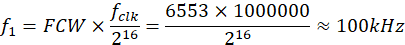
观察效果：
NCO 每个时钟周期将相位累加器加 6553，输出波形是 100kHz 正弦波。

调制过程：
如果你把频率控制字变成 13106（翻倍），频率变成 200kHz。
频率控制字变成 3276，频率变成 50kHz。

总结：频率调制就是控制这个相位增量，让输出波形的频率变快或变慢。

相位调制 (Phase Modulation) 示例

仍然使用固定频率控制字 6553（频率 100kHz）

在某一时刻，给相位累加器当前值加一个 相位偏移，比如加 16384（相位范围是 0~65535，16384约等于1/4周期的相位偏移）

观察效果：
输出波形的相位整体“提前”了 1/4 周期，相当于波形整体向左平移了 2.5μs（100kHz的波长是10μs，1/4就是2.5μs），但频率保持不变。

调制过程：
你可以动态改变相位偏移值，产生相位跳变、相位调节，波形看起来“瞬时位移”。

2、Multi-Channel NCO

功能：
让一个 NCO IP 同时支持多个“虚拟”NCO 通道，每个通道可以有独立的相位累加器状态，但共享同一套正弦/余弦查找表（LUT）和硬件资源。

原理：

• 在普通 NCO 里，相位累加器状态是唯一的，每个时钟更新一次。
• 在 Multi-Channel 模式下，内部会为每个通道维护一个独立的相位寄存器，并用多路复用器（MUX）按通道轮流送入相位增量器和 LUT。
• 这样做可以用一套硬件轮流为多个通道产生信号，节省 FPGA 资源。

应用场景：

• 多音信号生成（比如 8 个不同频率/相位的载波）
• 多通道通信系统（每个通道都有自己的调制/解调载波）

注意事项：

• 输出是时分复用的，每个通道的更新速率 = NCO 时钟 / 通道数
• 如果通道数多，单个通道的采样率会降低

3、Frequency Hopping

功能：
在运行过程中快速切换 NCO 的输出频率（跳频），并且切换时保持相位连续（或可选相位重置）。

原理：

• 普通 NCO 固定使用一个 phase_inc（相位增量）
• Frequency Hopping 模式会提供一个频率表（多个 phase_inc 值）
• 你可以在运行中选择表中的不同频率索引，NCO 会立即加载新的相位增量
• 如果选择了相位连续模式，切换频率时不清零相位累加器 → 波形不会出现相位跳变
• 如果选择了相位重置模式，切换时会清零相位累加器 → 波形从头开始

应用场景：

• FHSS（频率跳变扩频）
• 多信道雷达扫频
• 短时间内切换多种载波频率

四、效果

Generation Algorithm使用small rom,系统开始时nco_rst_n和nco_clken复位，第二个时钟开始工作，可以看到nco_out_valid_nc从cursor1到cursor2经过10个时钟开始有效，与如下用户手册说明一致。

Generation Algorithm使用CORDIC时，可以看到nco_out_valid_nc从cursor1到cursor2经过27个时钟开始有效，且能看出该算法杂散较大。