FPGA/Quartus学习日志（2）：NCO原理

原创已于 2025-10-19 10:57:59 修改 · 690 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#fpga开发 #学习

于 2025-10-18 21:04:36 首次发布

一、相位累加器（Phase Accumulator）

一个 N位寄存器，每个时钟周期累加一个数值，称为 频率控制字（FTW, Frequency Control Word）。
累加值越大，频率越高。
相位累加器的输出是一个 当前相位值（Phase），它决定了波形的位置。
累加器输出不是频率，而是波形的“相位角”。

频率控制字（FCW）是一个用于控制相位累加器增长速度的数字量。

通俗说：FCW 决定了输出信号的频率是多少。

它控制的是 每个时钟周期 相位累加器加多少，也就是 每一步“相位步长”。

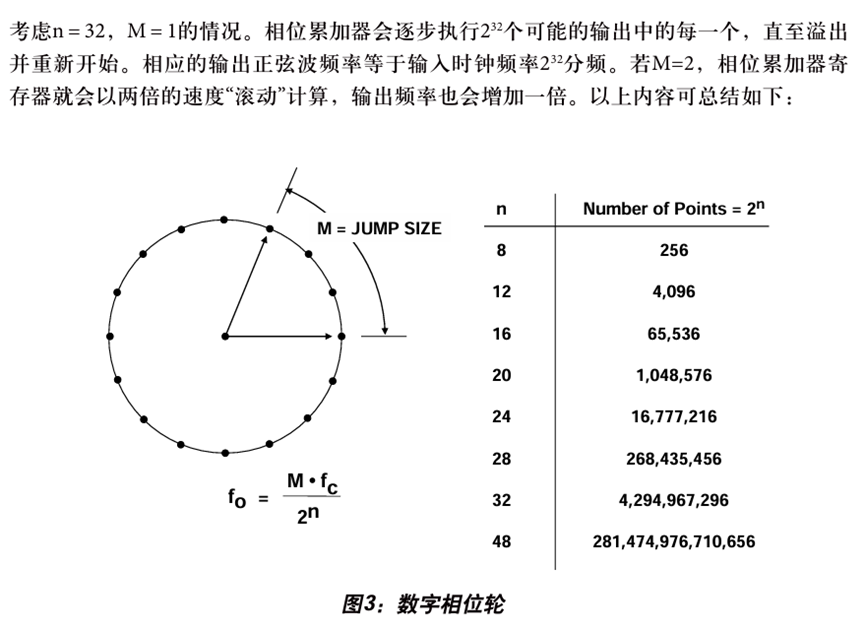
图中的M就是FCW，可以想见通过这种方式产生的实际上是阶梯状的正弦波。

输出频率公式

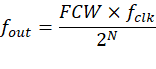
f_clk 为系统时钟；
FCW 为频率控制字；
N 为累加器位宽；
f_out 为输出频率。

举例说明

假设：

相位累加器宽度：32 位
FCW：例如 0x1000_0000
采样时钟：100 MHz

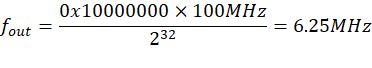
二、波形查找表（LUT ,Look-Up Table）

通常是 正弦波表，你可以用ROM或RAM存一整周期的离散波形数据（例如0~360°对应256个采样点）。
相位值的高位（例如N位中的前M位）作为查找表的地址。
输出的是 当前相位对应的波形值（例如sin值）。

三、工作原理

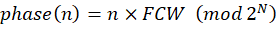
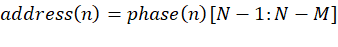
N 是相位累加器宽度（如 32bit）
M 是波形查找表地址位数（如 10~12bit）
截断后的高位送入 LUT，意味着低位的信息丢失！想象你每次只跳几个固定的地址（如高 10bit 每次变一点点），这样很多低位被“截断”了。

影响	描述
波形周期对不齐	输出周期非整数个样本
谐波失真	除主频以外出现杂散频率成分（spurs）
信号质量下降	SFDR（杂散动态范围）下降
频率分辨率受限	受限于相位累加器位数与 LUT 宽度

那为什么只取高若干位做查找表地址，而不是全部？

NCO核心目的：用相位表示频率 → 查出一个波形点

相位累加器越长，频率分辨率越高（输出频率的步进越小）：

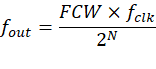
比如 N = 32，频率分辨率是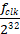，非常细。

但是我们查正弦波表的时候，没必要有那么多点 —— 通常只查一个 1024 点（10bit）或 256 点（8bit） 的表。

如果用全部位查表

问题	说明
表太大	用全部位查表资源爆炸（不可行）
地址太敏感	相位小变化会导致地址剧烈跳变
并没有更高分辨率	表项再多也没用，因为输出 DAC 位数、LUT精度是固定的

所以只取高若干位

减少查找表大小（节省资源）

32bit 相位 → 表要有 2^32=4Gb项，根本不可行
只用高 10 位查表 → 表大小为 2^10=1Kb项，可接受

高位代表“粗粒度的相位”，不会因低位抖动而频繁变化

低位变动频繁（例如累加器每次只变动1），查表地址会跳来跳去；
只取高位可以保证查表地址有足够平滑的相位步进。

查表地址的平滑跳动对应输出频率

查表间隔越大（即 FCW 越大），相位累加器跳得越快，输出频率越高；
所以只取高位，仍能正确表达频率调节，只是有一定位量误差（杂散源头之一）。

三、思维误区

1、认为查找表（LUT）中存的是一个被采样过的正弦波，采样率可能是某个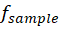

纠正：这是一个直觉陷阱。

NCO LUT 不是采样器，是一个近似器

直观错误：NCO 用一个 固定的正弦模板（LUT），然后以不同“速度”查表 ⇒ 频率变了，但“模板”没变，就好像用相同的波形片段，不同速率去“重放” ⇒ 感觉像是对波形下采样后输出

首先必须澄清：

查找表中存的不是“某个频率信号的采样点”，而是一个完整单位正弦波的周期离散化表示。

举例说明：

假设 LUT 有 256 个点（8-bit 相位累加器高 8 位作为地址），存的就是：

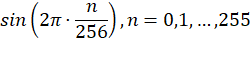
这是一整个单位正弦波的一个周期被等间隔量化了 256 个点，不带具体频率。它是一个“形状模板”，而不是某个采样频率下的数据记录。

NCO 的本质不是“回放原始波形”，而是“控制查找步进”生成新频率

可以理解为：在查表时跳过一定数量的点，从而控制生成的正弦信号的“频率”。

FCW = 1 ⇒ 每次查一个点 ⇒ 输出一个完整周期要花 256 个时钟 ⇒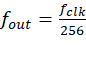

FCW = 2 ⇒ 每次查两个点 ⇒ 128 个时钟生成一周期 ⇒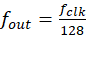

如果 FCW 很大，比如 FCW = 200，那么你每次跳 200 个相位点，就很快就绕一圈 ⇒ 输出频率也就高。

同时，NCO 也不是“数字下采样”，它本质是数字相位合成与查表输出，而不是对已有信号进行下采样。

DDS也要遵守奈奎斯特采样定理

如果设置过高的 FCW，就会超出奈奎斯特频率 ⇒ 导致混叠（aliasing）

这是 DDS 中非常重要的一条原则：

DDS 产生的输出频率不能超过 fclk/2，否则会混叠成错误的频率分量。

所以虽然查表可以任意跳步，但最终信号仍然是以系统时钟输出的采样序列，频率再高也不能超过采样率一半（这是采样定理的基本限制）。

特性	NCO	数字下采样
输入信号	无输入，是合成信号	有输入信号
输出频率变化方式	改变 FCW 控制频率	改变抽取因子 M
是否需要低通滤波器	不需要（除非外部采样）	需要（避免混叠）
是否违反采样定理	会混叠，不能超过 f_clk/2	会混叠，必须滤波
是否对已有信号进行处理	否	是