FPGA/Quartus学习日志（1）：FIR_IP_CORE

一、Option Instruction

1、Show Coefficient Bank

Coefficient Bank

• FIR 滤波器的运算本质就是输入样本和系数（Coefficient）做乘加运算。
• 这些系数会存放在一个系数存储区（Coefficient Bank）中。
• 系数可以是固定的（Static）——设计时写死在 IP 中，也可以是可重载的（Reloadable）——运行时由外部逻辑写入。

• 如果勾选，它会在配置页面展开一个系数表格，让你可以直接看到每个系数的数值。
• 如果你选择了可重载系数（Coefficient Reload）功能，这个表格也会显示多个 Bank（比如 Bank0、Bank1、Bank2…），方便设计时配置不同滤波器版本。

典型用途

做多速率滤波器（multirate FIR）或多通道滤波器时，可以在不同的 Bank 中放不同的系数组，实现快速切换滤波器特性（例如不同带宽、不同通带频率）。

2、Symmetry Mode

主要是用来设置 FIR 系数是否具有对称性，从而让 IP 核在硬件实现上进行优化

• None（无对称性）系数表完全按输入使用，不做对称优化。
• Automatic（自动检测）工具会检测你提供的系数文件，如果满足对称关系，会自动应用对称优化。

3、Flow Control

• IP核在输入/输出数据流动时的一种机制，让上游/下游模块能互相协调数据读写节奏，避免数据丢失或溢出。
• 如果启用流控，IP核会根据自身处理能力和内部FIFO状态，给出“准备好”或“暂停”的信号，告诉数据发送端或接收端什么时候可以传输数据（这就是所谓的 back pressure，即“反压”）

Back Pressure Support（背压支持）

•  Back Pressure 直译为“反压力”，是数据流中一种反馈机制。
•  当模块内部缓冲区快满，或者处理不过来时，它会向数据源（上游模块）发出“暂停”信号，要求暂停发送数据，防止数据溢出。
• 启用 Back Pressure Support，就是开启这种动态节奏控制，让系统各模块之间能够自动调节数据流，保证数据传输的可靠性和稳定性。

举例说明

假设你有两个模块，模块A发送数据到模块B。

• 如果模块B处理速度慢，它会通过back pressure告诉模块A“先别发了，我还没准备好”。
• 如果没开启back pressure，模块A会一直发数据，可能导致模块B溢出，丢数据。

二、整体框架

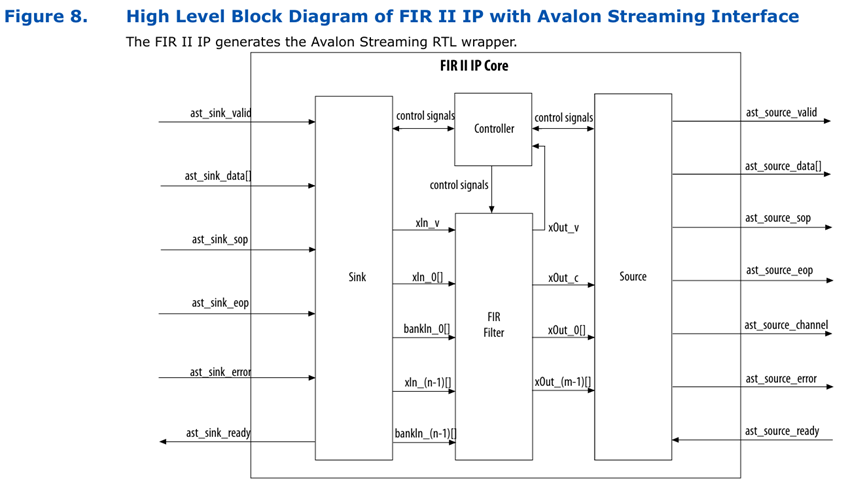
三、Structure

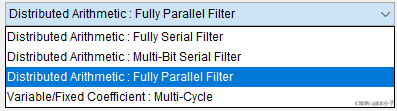
DA（Distributed Arithmetic，分布式算法）是 FIR 滤波器在硬件实现中常用的一种方法，特别适合 FPGA/ASIC 场景。

标准的 FIR 滤波器公式

                                                      

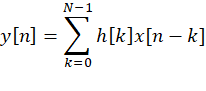
这里需要 N 次乘法 + N-1 次加法。在硬件上乘法器代价很大，尤其是 FPGA 上，如果用大量 DSP 资源来实现，会消耗很多逻辑和功耗。

1、DA 的核心思想

• 系数 h[k] 固定（常数）；
• 输入 x[n-k] 是二进制补码，可以按 逐比特拆分；
• 预先把所有可能的输入比特组合对应的部分和 存储在查找表 LUT 里；
• 每次取输入的一位，查 LUT 得到部分和，再加权累加。

以 x[n-k] 量化为B位补码二进制数，小数点位于最低位后面为例，即

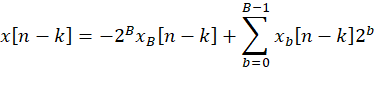
(1)输入展开

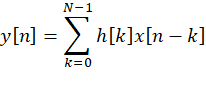
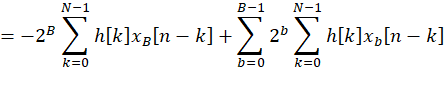
（2）查表

两个加数子式的内层形式均为

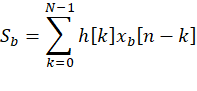
对于每一组

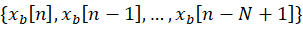
其实就是一个 N 位的比特向量。

• 对应的可能情况有

  

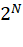
• 可以提前算好这些加权和（只和系数 h[k]  有关，不随输入变化）。
• 把这些结果存在一个查找表（LUT）里。

2、DA 的优势

• 不需要乘法器，只用移位、查表和加法。
• 非常适合 FPGA，因为 LUT 正好和 FPGA 的查表逻辑对应。
• 对于高阶 FIR，可以通过分块（分段 DA，Segmented DA）来减少 LUT 规模。

3、DA 的局限

• LUT 的大小随滤波器阶数呈指数增长（2^N），高阶 FIR 会爆炸。 所以常常用分块 DA，把 N 个系数分成小组，每组做一个小 LUT，然后部分和再累加。
• 系数必须固定（或很少更新），否则 LUT 需要频繁重建。

4、DA 的不同架构

DA 本质是“用 LUT + 移位 + 累加”来做 FIR，但 LUT、累加的使用方式不同，就衍生出几种架构：

（1）全并行 DA

结构特点：

• 每个输入样本的所有比特 同时送进 LUT。
• LUT 大小取决于滤波器阶数（比如 16 阶需要 2^{16} 这么大，不现实）。
• 解决方法是拆成多个小 LUT，然后并行加法器树累加。

优点：速度最快（一拍一个结果）

缺点：LUT 和加法器资源消耗大（FPGA 上用很多 BRAM + 逻辑资源）。

(2) 全串行 DA

结构特点：

• 输入样本逐比特（LSB → MSB）依次送入。
• 每个时钟只处理一位，依靠移位寄存器和累加器逐步形成输出。
• LUT 可以很小（比如只存几位组合）。

优点：硬件资源最省（LUT 小、加法器少）。

缺点：速度最慢（一个输出需要多个时钟周期）。

(3) 部分并行 DA

折中方案：

• 把输入按比特分组，比如 4 位并行处理。
• LUT 大小和速度都在串行与并行之间。
• 常用于 FPGA，利用 DSP Slice + LUT 实现。

四、关于pipeline level机制

以系统时钟8000Hz,滤波器配置Distributed Arithmetic : Fully Parallel Filter，pipeline level=0，coefficients=39为例。

如上图所示，输入一个克罗内克δ信号，可以观察到输出延迟9个时钟。

（pipeline level=1，输出延迟18个时钟；pipeline level=2，输出延迟26个时钟；pipeline level=3，输出延迟34个时钟）

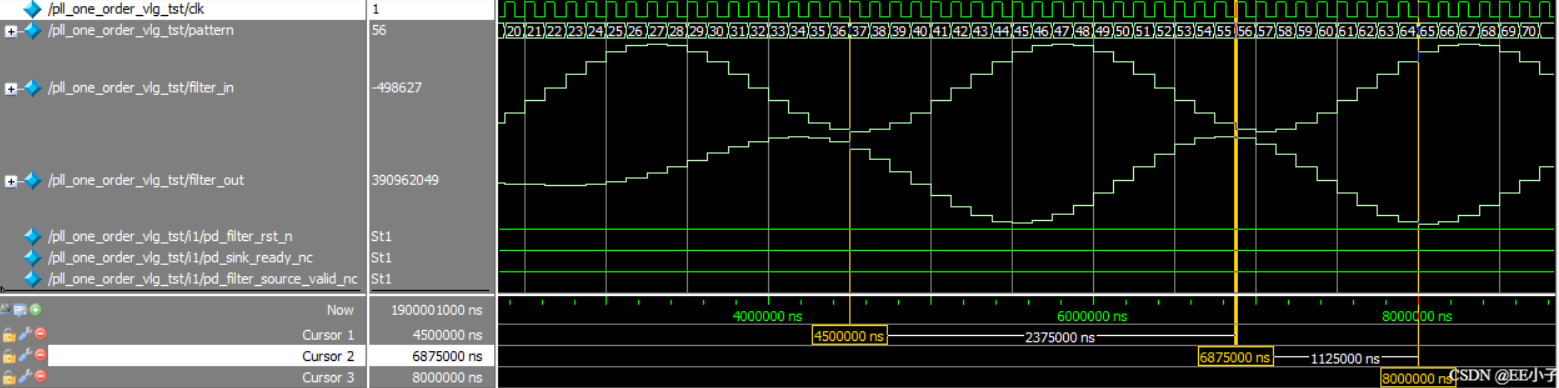
如上图所示，输入一个400Hz正弦信号，cursor3先向前9个时钟周期至cursor2，抵消滤波器实现结构带来的延时，再向前19个时钟周期至cursor1，可看出时序上输出可以与输入对齐。

但是pipeline level的机制没有弄清，查阅user guide，可能与如下说明有关

五、补充

关于MATLAB生成滤波器的系数量化后作为coefficient

假定量化位宽m位

浮点系数的 DC 增益(MATLAB提供的归一化)

 

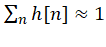
量化缩放因子

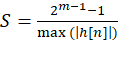
量化系数和

  

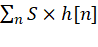
表示滤波器对恒定 DC（或低频）输入的增益放大倍数

量化系数绝对值和

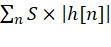
用于最坏情况的累加器容量（位宽）估算