高等数学——讲透求极限两大方法，夹逼法与换元法

本文始发于个人公众号：TechFlow

今天的文章聊聊高等数学当中的极限，我们跳过极限定义以及一些常用极限计算的部分。我想对于一些比较常用的函数以及数列的极限，大家应该都非常熟悉。

大部分比较简单的函数或者数列，我们可以很直观地看出来它们的极限。比如$\frac{1}{n}$，当n趋向于无穷大的时候，$\frac{1}{n}$的极限是0，再比如当n趋向于无穷大的时候，$n^2$的极限也是无穷大，等等。但是对于一些相对比较复杂的函数，我们一时之间可能很难直观地看出极限，因此需要比较方便计算极限的方法，今天的文章介绍的正是这样的方法——夹逼法和换元法。

夹逼法

夹逼法在数学领域其实非常常用，在中学的竞赛当中经常出现。夹逼法的原理非常简单，对于某一个函数f(x)，我们知道它的表达式，但是很难确定它的范围。我们可以先找到另外两个范围比较容易确定的函数g(x)和h(x)，然后证明:$g(x)\le f(x)\le h(x)$。通过h(x)和g(x)的范围来夹逼f(x)的范围。

说白了，就是直接求解不方便的函数，我们通过用其他容易计算的函数来替代的方法来间接求解，类似于“曲线救国”。

明白了夹逼法的概念之后，我们再来看一下它在数列极限当中的应用。当下存在数列{xn}\{x_n\}{xn​}我们需要确定它的极限，我们找到了另外两个数列{yn}\{y_n\}{yn​}和{zn}\{z_n\}{zn​}。如果它们满足以下两个条件：

1. $\exists n_0\in N$，当$n>n_0$时，有$y_n\le x_n\le z_n$。
2. $\underset{n\to +\infty }{\lim }{y}_n=a,\underset{n\to +\infty }{\lim }{z}_n=a$

那么，数列{xn}\{x_n\}{xn​}的极限存在，并且$\underset{n\to +\infty }{\lim }{x}_n=a$。从直觉上来看，上面的式子应该非常直观，但是我们还是试着从数学的角度来证明一下，顺便回顾一下极限的定义。

证明过程如下：

根据极限的定义，对于数列{xn}\{x_n\}{xn​}而言，对于任意$ϵ$都存在$n_0>0$，使得对于任意：$n>n_0$，都有$|x_n-a|<ϵ$。那么就称数列{xn}\{x_n\}{xn​}的极限是a。

由于数列{yn}\{y_n\}{yn​}的极限是a，所以存在$n_1$使得$n>n_1$时，$|y_n-a|<ϵ$。同理，存在$n_2$使得$n>n_2$时，$|z_n-a|<ϵ$。那么对于$n>max(n_1,n_2)$显然应该有：$|y_n-a|<ϵ$并且$|z_n-a|<ϵ$。

我们将绝对值展开，可以得到：

$$\begin{array}{rl}a-ϵ& <y_n<a+ϵ\\ a-ϵ& <z_n<a+ϵ\end{array}$$

我们代入$y_n\le x_n\le z_n$，可以得到：

$$\begin{array}{r}a-ϵ<y_n\le x_n\le z_n<a+ϵ\\ |x_n-a|<ϵ\end{array}$$

根据极限的定义，显然可以得到数列{xn}\{x_n\}{xn​}的极限也是a。

我们利用这个方法来看一个书上的例子，我们都知道当x趋向于0的时候，$x$和$\sin x$都趋向于0，但是$\frac{\sin x}{x}$的极限是多少呢？如果猜测一下，两个无穷趋向于0的极限的比值应该是1才对，但是这个只是我们的直观猜测，想要严格证明，还需要使用数学方法。

这个证明就用到了我们刚才说的夹逼法，并且非常巧妙，让我们来看一张下面这张图。

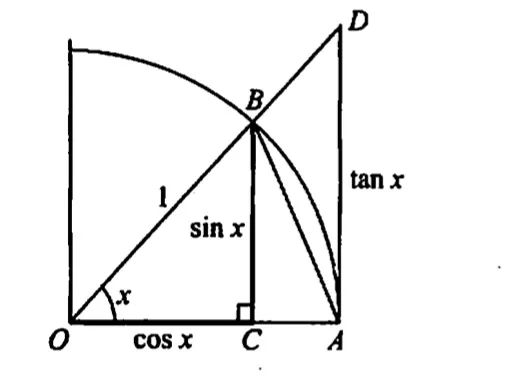
我们假设夹角$\angle AOB=x$，这里采用弧度制。我们令圆心OB的长度等于1，那么$BC=\sin x$，$OC=\cos x$，$AD=\tan x$。我们下面要用这张图里的几何图形的面积关系，显然：

$△AOB$的面积 < 扇形AOB的面积 < $△AOD$的面积。

$△AOB$的面积等于$\frac{1}{2}\ast OA\ast BC=\frac{1}{2}\sin x$，$△AOD$的面积等于$\frac{1}{2}\ast OA\ast AD=\frac{1}{2}\tan x$。这两个都很容易得出，直接套用三角形面积公式即可。扇形的面积看起来麻烦一些，但其实也很简单，在几何当中，扇形可以看成是特殊的三角形。我们把弧长看成是底面，半径可以看成是高，那么扇形的面积等于$\frac{1}{2}\ast 弧长\ast 半径$。所以扇形AOB的面积等于$\frac{1}{2}\ast x\ast 1=\frac{1}{2}x$。

我们列出来，可以得到：

$$\frac{1}{2}\sin x<\frac{1}{2}x<\frac{1}{2}\tan x$$

即：

$$\sin x<x<\tan x$$

其中$\tan x=\frac{\sin x}{\cos x}$，所以我们可以不等号两边同时除以$\sin x$，得到：

$$1<\frac{x}{\sin x}<\frac{1}{\cos x}$$

由于当x趋向于0的时候$\sin x,\cos x$都大于0，所以我们可以对不等式互换分子分母，得到：

$$\cos x<\frac{\sin x}{x}<1$$

到这里已经结束了，因为我们根据余弦的函数图像可以很容易看出来，当x趋向于0的时候，cosx趋向于1.但为了严谨起见，我们当做不知道这点，继续用数学的方法证明：

我们来计算当x趋向于0的时候，$1-\cos x$的取值范围，当x趋向于0的时候$\cos x<1$，所以$1-\cos x>0$。我们再对$1-\cos x$变形，这里要引入三角函数当中的和差化积公式：

$$\cos \alpha -\cos \beta =-2\sin \frac{\alpha +\beta }{2}\sin \frac{\alpha -\beta }{2}$$

由于$\cos 0=1$，带入和差化积可以得到：

$$\cos 0-\cos x=-2\sin \frac{x}{2}\sin -\frac{x}{2}=2{\sin }^2\frac{x}{2}$$

我们之前通过面积表示的方法已经证明了当x趋向于0的时候$\sin x<x$，所以$2{\sin }^2\frac{x}{2}<2\ast (\frac{x}{2}{)}^2=\frac{x^2}{2}$。当x趋向于0的时候，显然$x^2$也趋向于0，所以我们可以证明$\cos x$的极限是1.

换元法

我们接着来看换元法，学名是复合函数的极限运算法则。定义如下：假设我们有$y=f[g(x)]$，我们令$u=g(x)$。如果$\underset{x\to x_0}{\lim }g(x)=u_0,\underset{u\to u_0}{\lim }f(u)=A$，并且在x趋向于$x_0$时，有$g(x)\ne u_0$，那么：

$$\underset{x\to x_0}{\lim }f[g(x)]=\underset{u\to u_0}{\lim }g(u)=A$$

我们使用极限的定义同样可以很方便地证明它的正确性，这里就不证明了，感兴趣的同学可以试着证明一下。

了解了符合函数的极限运算法则之后，我们再来看一个例子巩固一下。

和上面的例子类似，我们这次求一下:$\underset{x\to 0}{\lim }\frac{1-\cos x}{x^2}$。

和上面那题一样，我们先使用和差化积对极限的分子进行变换，可以得到：

$$\underset{x\to 0}{\lim }\frac{2{\sin }^2\frac{x}{2}}{x^2}=\frac{1}{2}\underset{x\to 0}{\lim }\frac{{\sin }^2\frac{x}{2}}{(\frac{x}{2}{)}^2}$$

如果通过极限本身的定义来计算这个式子还是蛮复杂的，很难直观地获得答案。这个时候就需要用上换元法了，我们令$u=\frac{x}{2}$，那么这个极限就可以转化成复合函数极限了。$u=\frac{x}{2},f(u)=\frac{\sin u}{u}$。因为当x趋向于0的时候，u也趋向于0，当u趋向于0的时候，$f(u)$趋向于1，所以最终的极限就是1.

通过夹逼法和复合函数的极限替换公式，我们可以很方便地求解一些看起来比较棘手的极限。这也是我们求极限的过程当中使用非常频繁的方法。虽然上文当中的公式看起来有些比较麻烦，但是方法本身并不难，只要沉下心来，一定可以看明白的。

原创不易，希望我的文章可以给你带来收获。扫码关注我的公众号，获取更多文章，你们的支持是我最大的动力。

参考资料

同济大学《高等数学》第六版

程序员的数学