线性代数精华2——逆矩阵的推导过程

最新推荐文章于 2025-06-24 19:58:57 发布
原创 最新推荐文章于 2025-06-24 19:58:57 发布 · 2.8k 阅读 · 3 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#线性代数 #机器学习

本文详细介绍了逆矩阵的定义和计算方法，通过伴随矩阵的性质证明了AA*=|A|I，讨论了非奇异矩阵与奇异矩阵的区别，并指出奇异矩阵无逆矩阵。此外，还提及在Python中如何利用numpy库计算逆矩阵。

本文始发于个人公众号： TechFlow

上一讲当中我们复习了行列式的内容，行列式只是开胃小菜，线性代数的大头还是矩阵。

矩阵的定义很简单，就是若干个数按照顺序排列在一起的数表。比如m * n个数，排成一个m * n的数表，就称为一个m * n的矩阵。

矩阵运算的相关性质不多，主要的有这么几点：

  1. 矩阵的加法有结合律和交换律
  2. 矩阵的乘法没有交换律
  3. m * n的矩阵乘上n * k的矩阵的结果是一个m*k的矩阵

很多人会觉得矩阵乘法比较复杂，不仅是计算复杂，而且经常会记不清运算的方法。会觉得复杂，可能只是因为我们将它当做了数学公式来生硬的记忆，而没有理解其中的原理。

我们不妨假设A和B分别是一个m * n和n * k的矩阵：


那么，

其中，

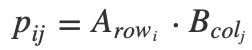
Arowi指的是A矩阵中第i行的行向量，同样Bcolj指的是B矩阵中第j列的列向量

最低0.47元/天 解锁文章
Numpy 中的矩阵求逆
何足道的博客
02-01 18万+
1. 矩阵求逆 import numpy as np a = np.array([[1, 2], [3, 4]]) # 初始化一个非奇异矩阵 print(a.I) print(np.linalg.inv(a)) #与上一步等同，对应于MATLAB中 inv() 函数 2. 矩阵求伪逆 import numpy as np # 定义一个奇异阵 A A = np.zeros((4,...
常用矩阵求导公式，逆矩阵求导
李宏宗的博客
02-24 3464
∂βx∂x=β\frac{\partial \beta \mathbf{x}}{\partial \mathbf{x}}=\beta∂x∂βx​=β ∂xTx∂x=2x\frac{\partial \mathbf{x}^T\mathbf{x}}{\partial \mathbf{x}}=2\mathbf{x}∂x∂xTx​=2x ∂xTAx∂x=(A+AT)x\frac{\partial \mathbf{x}^TA\mathbf{x}}{\partial \mathbf{x}}=(A+A^T)\mathbf
Numpy 中的矩阵求逆实例
12-25
1. 矩阵求逆 import numpy as np a = np.array([[1, 2], [3, 4]]) # 初始化一个非奇异矩阵(数组) print(np.linalg.inv(a)) # 对应于MATLAB中 inv() 函数 # 矩阵对象可以通过 .I 更方便的求逆 A = np.matrix(a) print(A.I) 2. 矩阵求伪逆 import numpy as np # 定义一个奇异阵 A A = np.zeros((4, 4)) A[0, -1] = 1 A[-1, 0] = -1 A = np.matrix(A) print(A) # print(A.I)
矩阵的逆的导数
颹蕭蕭
10-09 1万+
矩阵的逆的导数怎么求？
逆矩阵求导
Bungehurst
05-06 4369
逆矩阵求导 推导：假设求矩阵M(t)−1M(t)^{-1}M(t)−1的导数，已知： M(t)M−1(t)=Iddt(M(t)M−1(t))=dIdtddt(M(t)M−1(t))=0dM(t)dt⋅M−1(t)+dM−1(t)dt⋅M(t)=0dM−1(t)dt⋅M(t)=−dM(t)dt⋅M−1(t)解得：ddt(M−1(t))=−M−1(t)⋅dM(t)dt⋅M−1(t) \\M(t)M^{...
矩阵转置相关公式_线性代数精华2——逆矩阵的推导过程
weixin_39940344的博客
11-22 1355
本文始发于个人公众号： TechFlow上一讲当中我们复习了行列式的内容，行列式只是开胃小菜，线性代数的大头还是矩阵。矩阵的定义很简单，就是若干个数按照顺序排列在一起的数表。比如m * n个数，排成一个m * n的数表，就称为一个m * n的矩阵。矩阵运算的相关性质不多，主要的有这么几点：1. 矩阵的加法有结合律和交换律2. 矩阵的乘法没有交换律3. m*n的矩阵乘上n*k的矩阵的结果是一个m*k...
3.【线性代数】——矩阵乘法和逆矩阵
sda42342342423的博客
02-13 1831
矩阵乘法的5种理解计算方式，如何求逆矩阵。
线性代数基础知识——常见矩阵的概念及其关系
qq_41685509的博客
12-18 3318
转置矩阵、伴随矩阵、逆矩阵的定义，及其关系。
线性代数——补充10—矩阵的伪逆
最新发布
Rhett_Butler0922的博客
06-24 650
对于任意矩阵AAA，它的伪逆AA^+AAAAAAA^+A = AAAAAAAAAAAAAAATAAAATAA(表示AAAA^+AA是对称的)AATAAAATAA(表示AAA^+AAA是对称的)满足这四个条件的伪逆是唯一的。在机器学习和统计学中，我们经常遇到线性回归问题，目标是找到一个线性模型yXwϵyXwϵ来最好地拟合观测数据。yyy是一个m×1m \times 1m×1。
使用numpy对矩阵进行求逆
龙进的博客
11-19 1万+
昨晚算一道线性代数的题目的时候，算了半天，答案错了。验算了一下，觉得错误应该是出在矩阵求逆的地方。但是真的求逆太慢了，（主要是头晕），那怎么办呢？ 突然想起numpy这个超强大的科学计算库，于是乎就用几行代码写了一个矩阵求逆的程序。 import numpy as np a = np.array([[1, 1, 1], [0, 0.5, -2], [0, 1, 1]]) print(a) print('-----------') print(np.linalg.inv(a)) 我输入的是一个3
numpy的矩阵求逆
qq_41978896的博客
11-03 1万+
numpy的矩阵求逆 numpy中有np.linalg.inv()方法可以直接求逆，但是有时候原矩阵是无法直接求逆的，强行使用该方法会导致较大的误差；这时可以使用SVD矩阵分解的方法，舍去相关特征： matrix u, s, v = np.linalg.svd(matrix, full_matrices=False)#截断式矩阵分解 inv = np.matmul(v.T * 1 / s, u.T)#求逆矩阵 ...
numpy 矩阵求逆_numpy 基础 —— np.linalg
weixin_39864387的博客
12-05 624
（1）np.linalg.inv()：矩阵求逆（2）np.linalg.det()：矩阵求行列式（标量）np.linalg.norm顾名思义，linalg=linear+algebralinalg=linear+algebra，normnorm则表示范数，首先需要注意的是范数是对向量（或者矩阵）的度量，是一个标量（scalar）：首先help(np.linalg.norm)查看其文档：norm(x...
Python中如何创建元素为ndarray的list
Codefmeister's BLOG
11-21 945
python如何使得list中的元素是ndarray 在一个代码实现时，会想要类似MATLAB一样，拥有一个struct类型的数组，数组中的每个cell都是一个ndarray。因为在某些维度上shape不同，所以不能整合为一个大的ndarray。 要实现上述需求，可以进行如下操作: targetList = [] targetList.append(ndarray) 这样即可获得由ndarray构成的list，可以进一步对list进行concatenate等操作再次整合。 ...
笔记：矩阵行列式求导以及矩阵的逆的求导
热门推荐
DengTseng的博客
12-12 2万+
笔记：矩阵行列式求导以及矩阵的逆的求导一、结论二、矩阵的行列式求导三、矩阵的逆的导数 一、结论 设A=(aij(t))n×nA=(a_{ij}(t))_{n\times n}A=(aij​(t))n×n​， d∣A∣dt=∣A∣tr(A−1dAdt)dA−1dt=−A−1dAdtA−1 \begin{aligned} &\frac{d |A|}{dt} =|A|tr\left(A^{-1}\frac{dA}{dt}\right)\\ &\frac{d A^{-1}}{dt} = -A^{-1
线性代数：转置矩阵（matrix transpose）和逆矩阵（matrix inverse）
youandme520的专栏
07-31 1万+
这一篇是为了后面着色效果的数学基础做积累，之前我们使用矩阵的大部分情况都是直接的仿射空间变换，就是仿射空间A变换到仿射空间B，使用矩阵也都是如下： 矩阵T*齐次坐标V = 齐次坐标V' 其计算细节也就是矩阵行与向量列的点积，其计算意义也就是获得新仿射空间中的坐标分量，也聊了很多了。 这次我们就来学两个矩阵的操作，一个是矩阵的转置操作（得到转置矩阵），一个是矩阵的逆操作（得到逆矩阵）。 ①.先看下数学上怎么定义转置矩阵的： 将...
numpy 矩阵求逆_一起学数据分析之NumPy(14)——线性代数
weixin_39806413的博客
11-27 372
import numpy as np线性代数线性代数(如矩阵乘法、矩阵分解、行列式以及其他方阵数学等)是任何数组库的重要组成部分。不像某些语言，通过 * 对两个二维数组相乘得到的是一个元素级的积，而不是一个矩阵点积。因此，NumPy提供了一个用于矩阵乘法的dot函数(既是一个数组方法也是numpy命名空间中的一个函数)：In [2]:x = np.array([[1.,2.,3.],[4.,5.,...
python numpy逆_如何用python的numpy模块求某矩阵的逆矩阵
weixin_39723920的博客
11-22 1908
python是一个很有趣的语言，可以在命令行窗口运行。python中有很多功能强大的模块，这篇经验告诉你，如何使用python的numpy模块创建矩阵，并求该矩阵的逆矩阵。工具/原料windows系统电脑一台python软件并安装numpy模块方法/步骤1第一步，点击键盘 win+r，打开运行窗口。在运行窗口中输入“cmd"，点击enter键，打开windows命令行窗口。2第二步，在window...
线性代数基础与MATLAB向量矩阵操作入门
事实上，几乎所有主流机器学习算法都建立在线性代数之上：从最简单的线性回归到复杂的深度神经网络，参数均以向量或矩阵形式存在，训练过程涉及大量矩阵分解、特征值计算、梯度传播等操作。因此，能否高效使用MATLAB...
评论 2
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值