题意
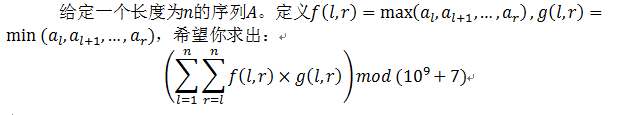
思路

代码
#include<cstdio>
#include<algorithm>
const int P = 1e9 + 7;
int n;
long long ans;
long long a[500001], minr[500001], maxr[500001];
long long minPre[500001], maxPre[500001], s[500001];
void solve(int l, int r) {
if (l > r) return;
if (l == r) {
ans = (ans + a[l] * a[l]) % P;
return;
}
int mid = l + r >> 1;
solve(l, mid);
solve(mid + 1, r);
minr[mid] = 1000000000;
s[mid] = maxr[mid] = minPre[mid] = maxPre[mid] = 0;
for (int i = mid + 1; i <= r; i++) {
minr[i] = std::min(minr[i - 1], a[i]);
maxr[i] = std::max(maxr[i - 1], a[i]);
minPre[i] = minPre[i - 1] + minr[i];
maxPre[i] = maxPre[i - 1] + maxr[i];
s[i] = (s[i - 1] + minr[i] * maxr[i]) % P;
}
long long minl = 1000000000, maxl = 0;
int u = mid, v = mid;
for (int i = mid; i >= l; i--) {
minl = std::min(minl, a[i]);
maxl = std::max(maxl, a[i]);
while (minr[u + 1] >= minl && u < r) u++;
while (maxr[v + 1] <= maxl && v < r) v++;
if (u < v) {
ans = (ans + (u - mid) % P * maxl % P * minl % P) % P;
ans = (ans + (minPre[v] - minPre[u]) % P * maxl % P) % P;
ans = (ans + s[r] - s[v]) % P;
} else {
ans = (ans + (v - mid) % P * maxl % P * minl % P) % P;
ans = (ans + (maxPre[u] - maxPre[v]) % P * minl) % P;
ans = (ans + s[r] - s[u]) % P;
}
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", &a[i]);
solve(1, n);
printf("%lld", ans);
}
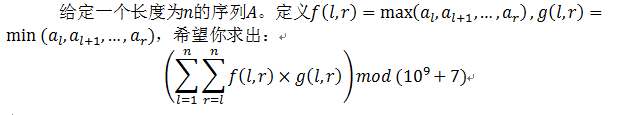






 本文介绍了一种高效算法,用于计算数组中每个元素与其右侧所有元素的最小值和最大值乘积之和,解决复杂的数据结构与算法问题。通过递归划分和动态规划技巧,实现O(n log n)的时间复杂度。
本文介绍了一种高效算法,用于计算数组中每个元素与其右侧所有元素的最小值和最大值乘积之和,解决复杂的数据结构与算法问题。通过递归划分和动态规划技巧,实现O(n log n)的时间复杂度。
















 543
543

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








