【LUT技术专题】LLFLUT++: 基于拉普拉斯金字塔的LUT方法

本文将围绕《LLFLUT++: High-resolution Photo Enhancement in Real-time: A Laplacian Pyramid Network》展开完整解析。论文提出LLF-LUT++ 端到端框架，通过拉普拉斯金字塔分解与重建融合全局和局部算子，结合图像自适应 3D LUT 与两种权重融合策略实现全局色调调整，借助空间 - 频率 Transformer 权重预测器 高效提取权重，利用图像自适应可学习局部拉普拉斯滤波器 细化高频分量边缘细节，在单 GPU 上实现 4K 图像 13ms 实时处理，在 HDR + 数据集上 PSNR 提升 2.64dB，在 MIT-Adobe FiveK 和 HDR + 两大基准数据集上，无论 480p 还是 4K 分辨率，其定量（PSNR、SSIM 等）和定性表现均优于现有先进方法。参考资料如下：
[1]. 论文地址
[2]. 代码地址

---

专题介绍

Look-Up Table（查找表，LUT）是一种数据结构（也可以理解为字典），通过输入的key来查找到对应的value。其优势在于无需计算过程，不依赖于GPU、NPU等特殊硬件，本质就是一种内存换算力的思想。LUT在图像处理中是比较常见的操作，如Gamma映射，3D CLUT等。

近些年，LUT技术已被用于深度学习领域，由SR-LUT启发性地提出了模型训练+LUT推理的新范式。
本专题旨在跟进和解读LUT技术的发展趋势，为读者分享最全最新的LUT方法，欢迎一起探讨交流，对该专题感兴趣的读者可以订阅本专栏第一时间看到更新。

系列文章如下：
【1】SR-LUT
【2】Mu-LUT
【3】SP-LUT
【4】RC-LUT
【5】EC-LUT
【6】SPF-LUT
【7】Dn-LUT
【8】Tiny-LUT
【9】3D-LUT
【10】4D-LUT
【11】AdaInt-LUT
【12】Sep-LUT
【13】CLUT
【14】ICELUT
【15】AutoLUT
【16】SA-3DLUT
【17】SABLUT
【18】SVDLUT

---

一、研究背景

照片增强的重要性不言而喻，其可以提升图像视觉美感。现有HDR 成像技术需依赖增强算子保留场景细节与色彩，但传统方法需工程师手动调整或专业软件精细修图，效率低。直接应用现有的图像增强方案存在以下的问题：

1. 基于学习的方法：性能强但计算量随图像尺寸线性增长，4800 万像素图像需海量计算资源（数百亿 FLOPs）和存储空间（超 20GB / 张）。
2. 混合方法（如 3D LUT 类）：高效低内存，但全局算子局部效果差，高分辨率图像下采样（最高 16 倍）导致细节丢失，最典型的例子是3D-LUT。

因此，论文提出兼顾实时性与高性能的高分辨率图像增强框架，解决全局与局部增强失衡问题。

思维导图如下所示：

二、LLFLUT方法

如标题所述，LLFLUT的核心思路是利用拉普拉斯金字塔分解与重建，在低频分量进行全局色调调整，在高频分量逐步细化局部边缘细节。它的网络整体流程图如下所示：

整体流程比较复杂，分为2个阶段，第一个阶段是粗增强，会增强得到2个输出，第一个是大图的粗增强结果$\bar{I}$以及下采样的增强结果${\bar{I}}_{\text{LR}}$。大图的粗增强结果会利用拉普拉斯分解出多个层，然后进行逐层的增强，底层还会使用canny算子来提取边缘，加入edge map的信息辅助，最终逐层向上融合得到增强结果$\hat{I}$。
下面将分阶段来讲解。

2.1 粗增强阶段

作者在粗增强阶段使用了2种方式，一种是不带空间感知的，另一种是带空间感知加权的，因为加了空间信息会增大计算量，所以是在小分辨率上用，不带的在大分辨率上使用，如下图所示：

（b）图展示的方式就是3D-LUT中使用到的方法，通过预测的weight加权得到一个最终的3DLUT作用到原始图像上。（c）图展示的是一个空间加权预测的方式，会推理出每一个lut的每一个点的权重，这样再进行加权，显然它会比前面一种方式更加复杂，计算量也更大，它的计算公式如下：$$\begin{array}{r}{O}_{(i,j,k)}^{h,w,c}={\Phi }^{h,w,c}\left(I_{(i,j,k)}^r,I_{(i,j,k)}^g,I_{(i,j,k)}^b,{\omega }^{h,w}\right)\\ ={\sum }_{t=0}^{T-1}{\omega }_t^{h,w}{M}_t^c\left(I_{(i,j,k)}^r,I_{(i,j,k)}^g,I_{(i,j,k)}^b\right)\end{array}$$其中$O_{(i,j,k)}^{h,w,c}$表示坐标$(h,w)$处通道$c$的输出像素值，${\omega }_t^{h,w}$为像素级权重图，$M_t^c$为第$t$个3D LUT基的映射函数，通过加权求和多个3D LUT基的映射结果，实现像素级的全局色调调整。
可见以上两个图像分别对应着大图的粗增强结果$\bar{I}$以及下采样的增强结果${\bar{I}}_{\text{LR}}$的计算过程。
为了实现这个过程，作者设计了如下的网络来实现这个操作，网络的输入是原图下采样的输入图像，因此计算量不会太大。

其中Learned weight points即大图所使用到的权重，而Learned Weight maps是小图所使用到的权重。其中的网络结构如下所示：

其中图(a)和图(b)分别代表Fourier-Swin Transformer encoder block和 basic Swin Transformer decoder block，是常见算子的一个组合，包含window的自注意力机制以及LN和FFT变换。
通过以上网络结构的设计，可以实现一个轻量级的粗增强过程，可以看到这部分很好的权衡了计算量和效果。

2.2 拉普拉斯金字塔增强阶段

摘出右半部分进行描述：

底层的输入有4个，最小分辨率的增强结果$I_{\text{LR}}$、最小分辨率经过canny算子提取的edge map、拉普拉斯金字塔的最后2层${\bar{l}}_n$和${\bar{l}}_{n-1}$，当然为了让他们分辨率一样还需要upsample的支持，他们会被concat到一起得到一个10输入通道的图，经过一系列网络处理后，得到两个逐像素的输出用于做refine，用于refine的操作叫做LLF Remapping Function，处理后可以得到增强后的高频细节${\hat{l}}_{n-1}$ 这个过程用公式描述：$${\hat{l}}_{n-1}=r\left({\overline{l}}_{n-1},g_{n-1},{\alpha }_{n-1},{\beta }_{n-1}\right)$$其中，${\bar{l}}_{n-1}$为分解得到的原始高频分量，$g_{n-1}$为对应层的参考值，${\alpha }_{n-1}$和${\beta }_{n-1}$为该层学习到的参数，$r(\cdot )$为可学习重映射函数，${\hat{l}}_{n-1}$为细化后的高频分量，用于保留局部边缘细节。

再往上的循环只是少了edge map的输入，其他的输入还是一样，因此输入是9个通道，通过不断的循环得到拉普拉斯金字塔复原的所有高频细节，最后跟最小分辨率的增强结果$I_{\text{LR}}$进行金字塔重建得到输出。

其中Remapping操作的公式如下：$$r(i)=\{\begin{array}{ll}g+\mathrm{sign}(i-g){\sigma }_r{\left(\frac{|i-g|}{{\sigma }_r}\right)}^{\alpha }& \text{if }i\le {\sigma }_r\\ g+\mathrm{sign}(i-g)\left(\beta (|i-g|-{\sigma }_r)+{\sigma }_r\right)& \text{if }i>{\sigma }_r\end{array}$$

描述传统局部拉普拉斯滤波器的像素值重映射规则，$i$为输入像素值，$g$为参考像素值，${\sigma }_r$为强度阈值（固定为0.1），$\alpha$和$\beta$为手动调参的形状参数，$\mathrm{sign}(\cdot )$为符号函数；该公式分两段定义像素值的非线性变换，实现局部边缘增强，我们在每一层的2个逐像素的输出就是这个形状参数，相当于自适应学习这个过程，而不是手工的调节。

2.3 损失函数

如下所示，包含几个损失函数：$${\mathcal{L}}_1=\sum _{i=1}^{H\times W}\left(\Vert \hat{I}[i]-R[i]{\Vert }_1+{\Vert {\hat{I}}_{LR}[i]-R_{LR}[i]\Vert }_1\right)$$定义框架的L1重建损失，$H\times W$为图像像素总数，$\hat{I}[i]$和$R[i]$分别为高分辨率增强图像与参考图像的第$i$个像素值，${\hat{I}}_{\text{LR}}[i]$和$R_{\text{LR}}[i]$为对应低分辨率图像的像素值；通过同时约束HR和LR图像的像素误差，保证增强结果的全局一致性。
$${\mathcal{L}}_p=\sum _l\frac{1}{H^l{W}^l}\sum _{h,w}{\Vert \varphi (\hat{I}{)}_{hw}^l-\varphi (R{)}_{hw}^l\Vert }_2^2$$计算感知层面的损失，$\varphi (\cdot )$为预训练特征提取网络（如AlexNet），$l$为网络的特征层索引，$H^l{W}^l$为第$l$层特征图的尺寸，$\varphi (\hat{I}{)}_{hw}^l$和$\varphi (R{)}_{hw}^l$分别为增强图像和参考图像在第$l$层$(h,w)$位置的特征值；通过约束特征空间的L2距离，提升增强图像的视觉感知质量。
最后总的损失函数是：$$\mathcal{L}={\mathcal{L}}_1+{\lambda }_s{\mathcal{L}}_s+{\lambda }_m{\mathcal{L}}_m+{\lambda }_p{\mathcal{L}}_p$$${\mathcal{L}}_1$为重建损失，${\mathcal{L}}_s$为平滑正则化项（${\lambda }_s=0.0001$），${\mathcal{L}}_m$为单调性正则化项（${\lambda }_m=10$），${\mathcal{L}}_p$为LPIPS感知损失（${\lambda }_p=0.01$）；通过加权融合多类损失，平衡“像素级精度”与“视觉感知质量”，同时保证3D LUT映射的平滑性和单调性，这个平滑性和单调性损失可看3D-LUT讲解。

三、实验结果

首先讲一下消融实验。实验结果如下图所示，结论如下：

1.组件有效性：像素级权重图、空间 - 频率 Transformer、可学习局部拉普拉斯滤波器等核心组件均能独立提升性能，全组件融合时性能最优（HDR+ 480p PSNR 达 28.43dB）。
2. 权重融合策略：组合 “权重点 + 权重图” 的融合策略优于单一权重点 / 权重图，PSNR 提升 1.32dB，兼顾效率与精度。
3. 金字塔层数：低频图像分辨率降至 64×64 时，性能仅下降 0.08dB，但计算量减少 30%，验证了自适应金字塔分解的合理性。

接着是定量实验。

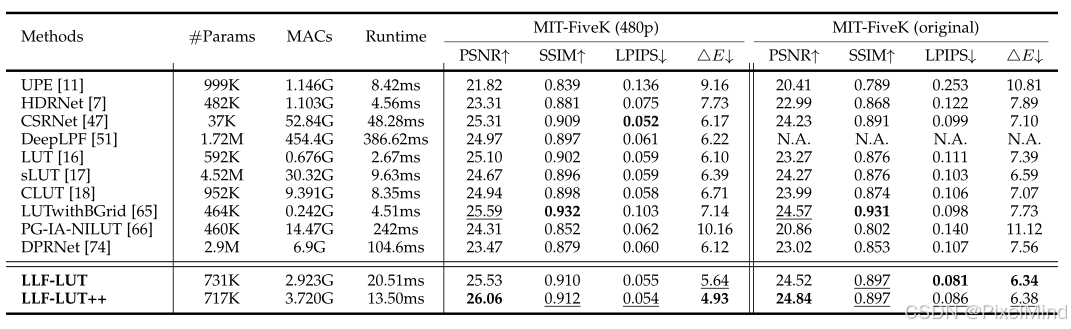
结论如下：

1. 在HDR+ 和MIT-Adobe FiveK两大基准数据集上，LLF-LUT++ 在 480p 和 4K 分辨率下，PSNR、SSIM（越高越好）、LPIPS、△E（越低越好）四项核心指标均全面优于现有先进方法（如 DPRNet、LLF-LUT、DeepLPF 等），验证了方法的高性能。
2. 相比基线模型 LLF-LUT，LLF-LUT++ 在参数减少 14K 的前提下，HDR + 数据集原始分辨率 PSNR 提升 2.64dB，MIT-Adobe FiveK 数据集原始分辨率 PSNR 提升 0.32dB，实现 “更少参数 + 更高性能”。
3. 480p 分辨率下，LLF-LUT++ 在 HDR + 数据集 PSNR 达 28.43dB（比 SOTA 方法 DPRNet 高 0.58dB），在 MIT-Adobe FiveK 数据集 PSNR 达 26.06dB（比 LLF-LUT 高 0.53dB），局部细节与色彩还原精度显著提升。
4. LLF-LUT++ 实现4K 高分辨率图像实时处理：单 NVIDIA Tesla V100 32GB GPU 上，4K 图像处理耗时仅 13.50ms / 张，远低于 DPRNet（104.6ms / 张）、DeepLPF（386.62ms / 张）等 SOTA 方法。
5. 平衡计算复杂度与性能：相比 LLF-LUT，LLF-LUT++ 虽 MACs 从 2.923G 增至 3.720G，但运行时间减少 7.01ms，且性能大幅提升，在 “效率 - 性能” 权衡中表现最优。
6. 低参数量优势：仅 717K 参数，远低于 DPRNet（2.9M）、DeepLPF（1.72M），具备边缘设备部署潜力。

然后是定性实验。


结论如下：

1. 细节保留：在草地纹理、水面灯光反射等复杂场景中，LLF-LUT++ 能精准保留高频细节，边缘清晰无模糊。
2. 色彩还原：在天空雾区、高动态范围场景中，颜色还原自然保真，无过曝 / 欠曝、色偏等问题。
3. 伪影控制：通过可学习局部拉普拉斯滤波器优化，有效避免传统方法的光晕伪影，视觉效果更自然。

四、总结

LLF-LUT++ 实现4K 图像 13.50ms / 张实时处理，参数 717K（比 LLF-LUT 少 14K）；在两大基准数据集上，480p 和 4K 分辨率的定量（PSNR 最高提升 2.64dB）与定性表现均优于现有 SOTA 方法；它融合全局与局部增强的设计，有效解决细节丢失和局部效果差的问题。
作者也给出了一些问题，例如可能受训练数据集偏见影响，存在潜在社会偏见风险；色彩转换具有主观性，难以满足所有用户偏好；比基础 3D LUT 计算量大（MACs 更高），直接用于视频会产生帧间闪烁。这些是以后优化的目标。

---

感谢阅读，欢迎留言或私信，一起探讨和交流，如果对你有帮助的话，也希望可以给博主点一个关注，谢谢。