1、向量的点乘的意义:
解决不同方向向量间存在的方向问题,不同方向的向量直接乘运算是没有意义的。通过投影的方式,让向量间指向同一方向,向量相乘起来才有了意义。向量的点乘结果为一个标量,向量点乘亦称为向量的内积。
在二维空间中,向量的内积有:u⃗⋅v⃗=∥u⃗∥⋅(∥v⃗∥⋅cosθ)\vec {u} · \vec {v}=\|\vec {u}\|·(\|\vec {v}\|·cos\theta)u⋅v=∥u∥⋅(∥v∥⋅cosθ)
2、向量点乘在分类上的反映
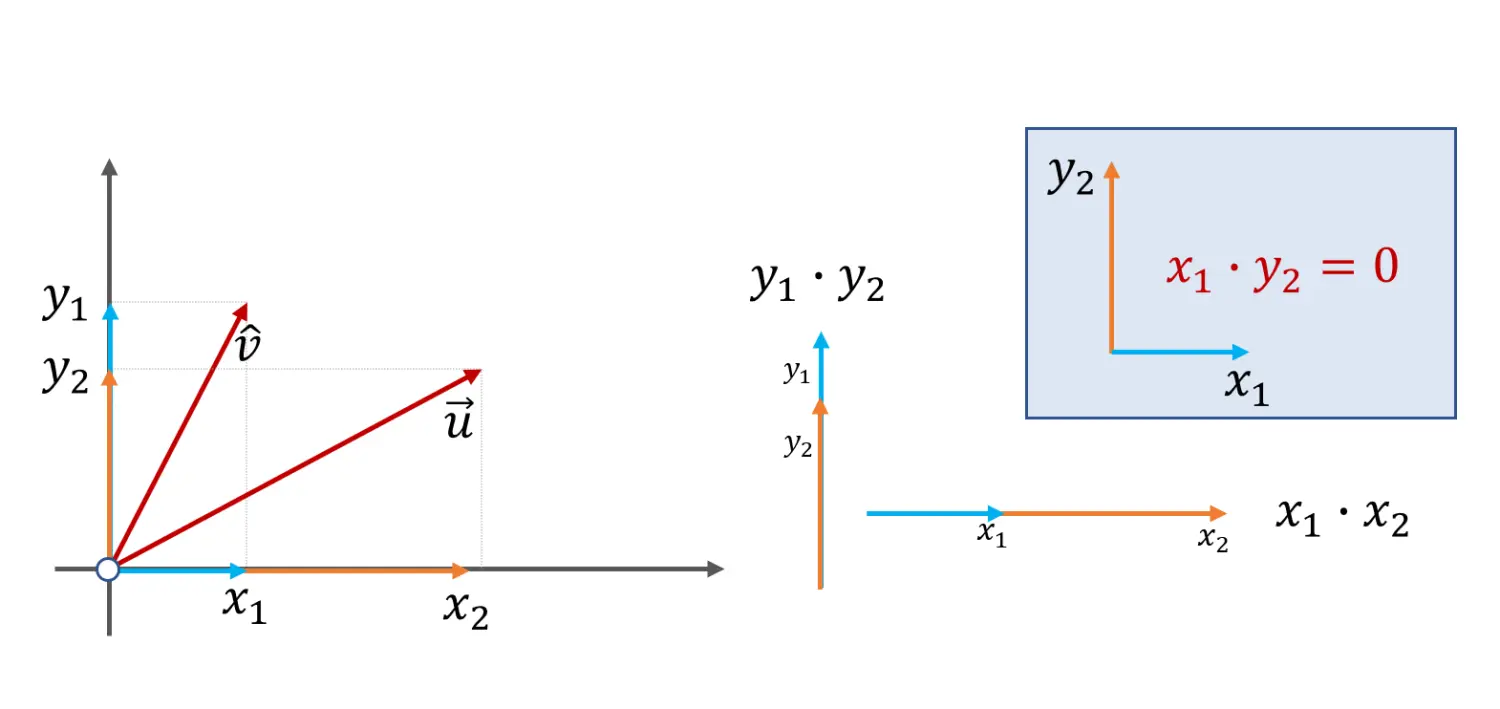
向量的点乘结果反映在分量上是向量间同属性分量的乘积的和,如u⃗⋅v⃗=x1⋅x2+y1⋅y2\vec {u} · \vec {v}=x_1 \cdot x_2 + y_1 \cdot y_2u⋅v=x1⋅x2+y1⋅y2,其中x1⋅x2x_1 \cdot x_2x1⋅x2与y1⋅y2y_1 \cdot y_2y1⋅y2分别是两向量u⃗,v⃗\vec {u} ,\vec {v}u,v在参考坐标系的基向量上的投影的乘积,当基向量互相垂直的情况下,两向量的不同属性的分量(如x1⋅yyx_1 \cdot y_yx1⋅yy)的相乘是无意义的,分量间的夹角θ=90∘\theta = 90^{\circ}θ=90∘,所以不同属分量乘积是0。
3、向量点乘的应用
主要用来计算向量间的夹角θ\thetaθ :cosθ=u⃗⋅v⃗∥u⃗∥⋅∥v⃗∥cos\theta=\frac {\vec u \cdot \vec v} {\|\vec u\| \cdot \|\vec v\|}cosθ=∥u∥⋅∥v∥u⋅v
向量夹角θ\thetaθ 可以用来衡量两个向量的相似程度(余弦相似度的应用)
[θ<90∘相似;θ=90∘无关;θ>90∘背离\theta < 90^\circ 相似 ; \theta = 90^\circ 无关 ; \theta > 90^\circ 背离θ<90∘相似;θ=90∘无关;θ>90∘背离]
→\rightarrow→应用领域如推荐系统,商品,电影,音乐的推荐





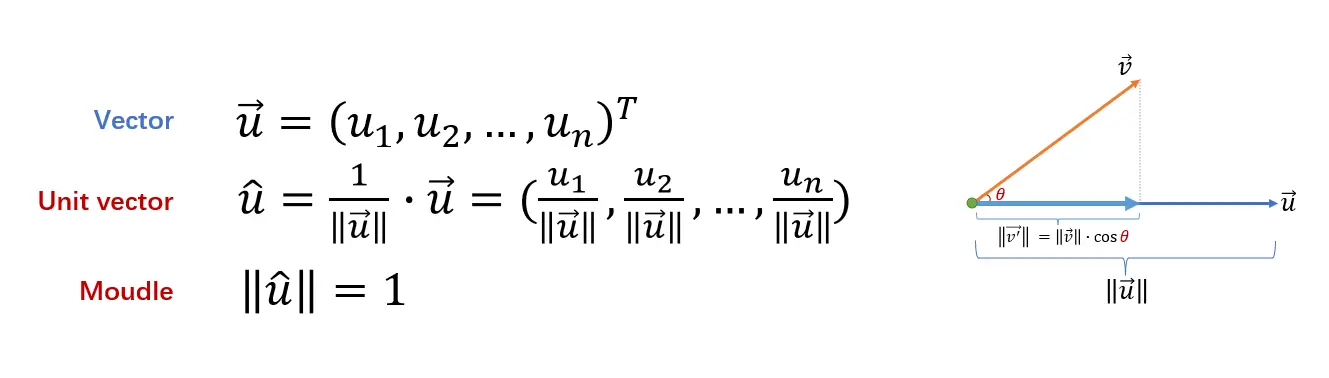


















 7200
7200

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










