向量 是对数的拓展,一个向量代表的是一组数; 矩阵 是对向量的拓展,一个矩阵代表的是一组向量。
矩阵形式的4种应用: 数据记录表,系统,变换函数和空间。
当矩阵 表示对一个系统的描述,因为系统可以通过方程组描述系统内成员变量的关系,方程组构成系统的描述矩阵,通过方程式可以求解系统的最优解。
矩阵与向量的乘法中T⋅u⃗=v⃗T \cdot \vec {u} = \vec {v}T⋅u=v,列向量u⃗\vec {u}u左乘矩阵TTT转换成了列向量v⃗\vec {v}v这种形式,矩阵TTT可以理解成是列向量u⃗\vec {u}u的转换函数,类似数字的函数形式(f(x)=yf(x)=yf(x)=y)。
矩阵的基本运算:
-
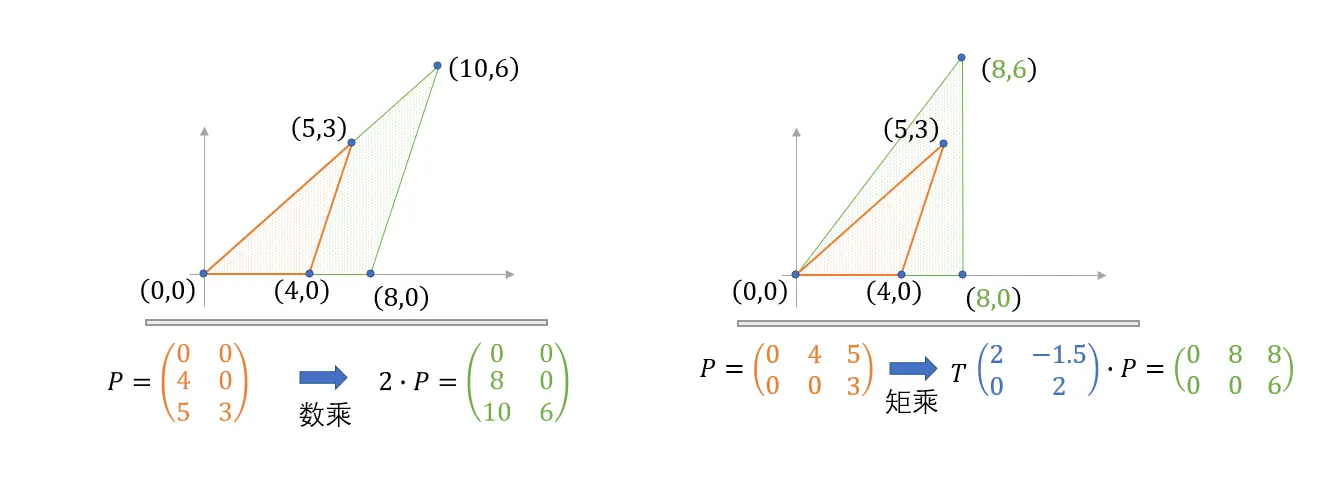
矩阵数乘 : k⋅A→k \cdot A \rightarrowk⋅A→ 图形学上理解为对不同分量进行kkk倍缩放;
-
矩阵矩乘 : Tm∗n⋅An∗k=Bm∗k→T_{m*n} \cdot A_{n*k} = B_{m*k} \rightarrowTm∗n⋅An∗k=Bm∗k→图形学上理解为对不同分量进行函数运算的不等倍变换。 矩阵乘法形式中,左乘矩阵TTT看作向量的处理函数,则被TTT变换的列向量构成右乘矩阵了AAA,矩乘结果是矩阵AAA的每个列向量由TTT变换后组成了矩阵BBB(如下图示):
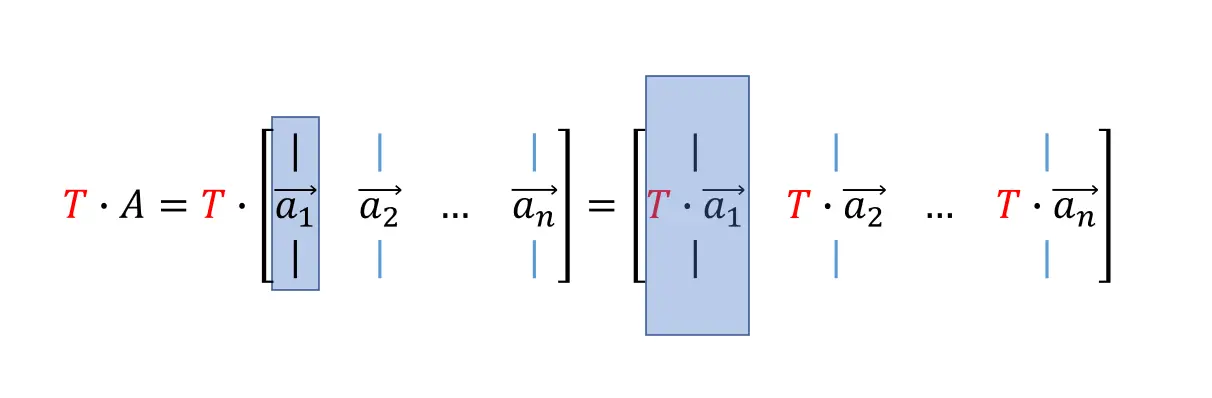
-
矩阵的幂:只有方阵才有幂,Ak={A⋅A⋅A⋯A}k,k≥1A^k = \{A \cdot A \cdot A \cdots A\}_k, k \geq 1Ak={A⋅A⋅A⋯A}k,k≥1
-
矩阵转置:行向量与列向量的相互转换,A=(aij)→AT=(aji)A=(a_{ij}) \rightarrow A^T=(a_{ji})A=(aij)→AT=(aji),性质:① (A+B)T=AT+BT(A+B)^T = A^T+B^T(A+B)T=AT+BT;②(A⋅B)T=AT⋅BT(A \cdot B)^T=A^T \cdot B^T(A⋅B)T=AT⋅BT
-
旋转变换矩阵TTT
$T = \begin{bmatrix} cos \theta & sin \theta \ -sin \theta & cos \theta \end{bmatrix} \rightarrow T \times P = (x^{'} , y{'})T $
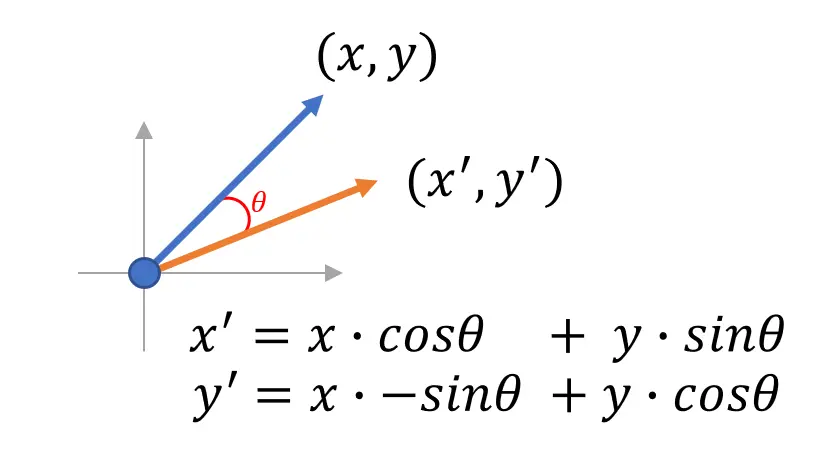
 矩阵的基本运算与应用
矩阵的基本运算与应用
























 1823
1823

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










